Содержание
- 2. Задача о вычислении площади плоской фигуры Решим задачу о вычислении площади фигуры, ограниченной графиком функции ,
- 3. Задача о вычислении площади плоской фигуры
- 4. Задача о вычислении площади плоской фигуры
- 5. Определенный интеграл
- 6. Определенный интеграл
- 7. Определенный интеграл
- 8. Теорема о существовании определенного интеграла
- 9. Свойства определенного интеграла
- 10. Свойства определенного интеграла
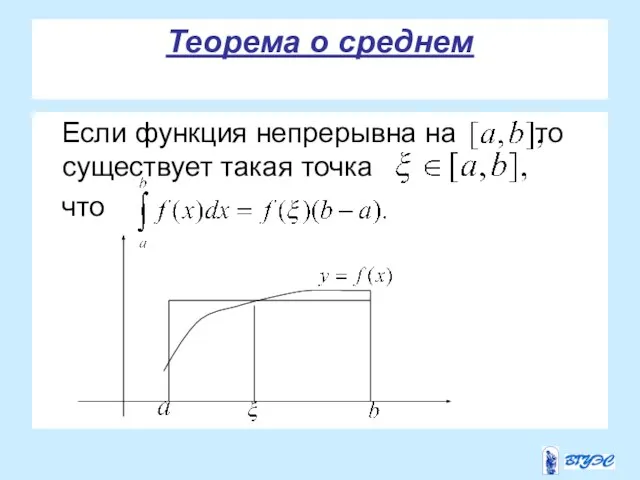
- 11. Теорема о среднем Если функция непрерывна на то существует такая точка что
- 12. Вычисление определенного интеграла
- 13. Пример Вычислить .
- 14. Вычисление интеграла
- 15. Пример
- 17. Пример
- 18. Несобственный интеграл
- 19. Пример . Вычислить несобственный интеграл (или установить его расходимость) . Этот несобственный интеграл расходится.
- 20. Пример Несобственный интеграл
- 21. Геометрические приложения определенного интеграла
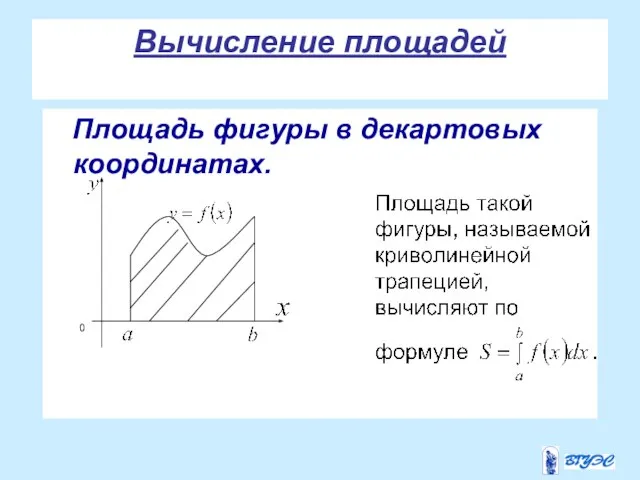
- 22. Вычисление площадей Площадь фигуры в декартовых координатах.
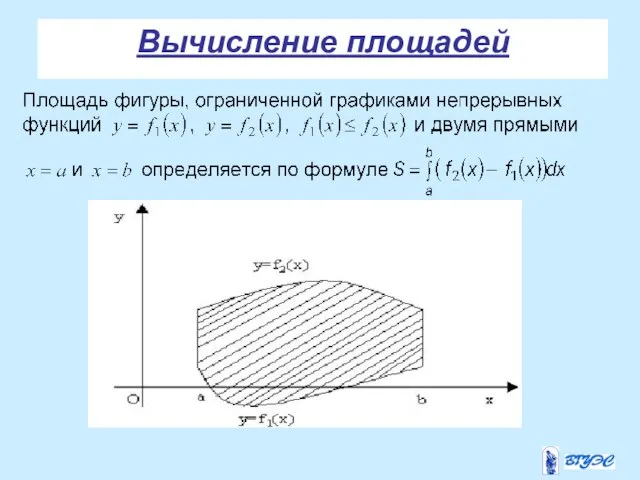
- 23. Вычисление площадей
- 24. Вычисление площадей В случае параметрического задания кривой, площадь фигуры, ограниченной прямыми , осью Ох и кривой
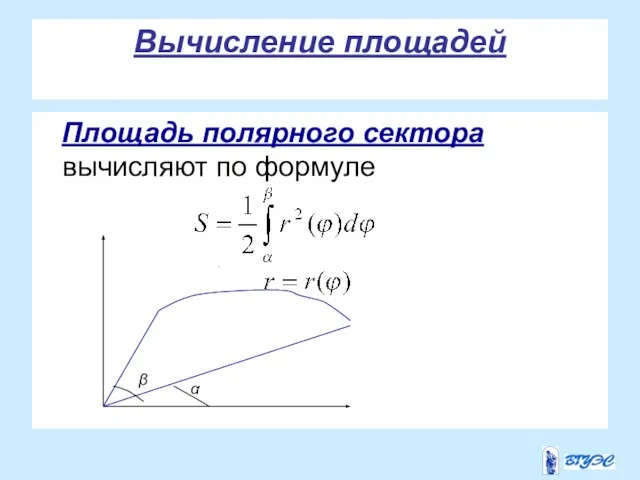
- 25. Вычисление площадей Площадь полярного сектора вычисляют по формуле . α β
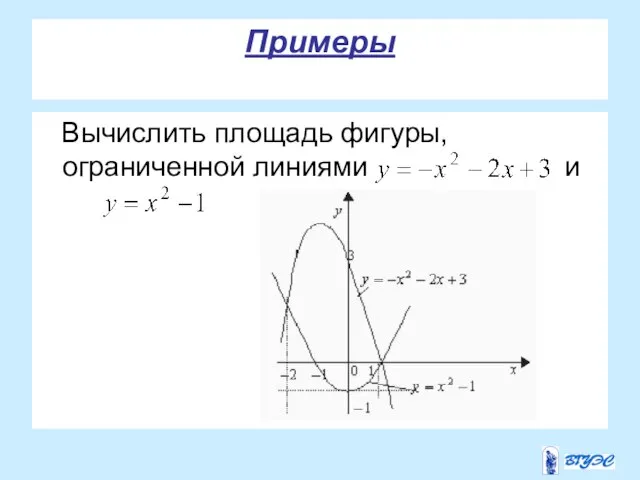
- 26. Примеры Вычислить площадь фигуры, ограниченной линиями и
- 27. Продолжение Получим
- 28. Примеры Найти площадь эллипса . Параметрические уравнения эллипса у о х
- 29. Пример Площадь фигуры, ограниченной лемнискатой Бернулли и лежащей вне круга радиуса :
- 30. Вычисление длины дуги Если кривая задана параметрическими уравнениями , , то длина ее дуги , где
- 31. Длина дуги в декартовых координатах Если кривая задана уравнением , то , где a, b–абсциссы начала
- 32. Длина дуги в полярных координатах Если кривая задана уравнением в полярных координатах , то , где
- 33. Примеры Вычислить длину дуги кривой от точки до . , тогда
- 34. Вычисление объема тела вращения. Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой ,
- 35. Вычисление объема тела вращения Объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривой , отрезком
- 36. Вычисление объема тела вращения Искомый объем можно найти как разность объемов, полученных вращением вокруг оси Ox
- 38. Скачать презентацию






























 Угол между прямыми
Угол между прямыми Неопределённый интеграл
Неопределённый интеграл Вычисление площадей и объемов. Лекция 5
Вычисление площадей и объемов. Лекция 5 Прямоугольный параллелепипед
Прямоугольный параллелепипед Построение цилиндра в изометрической проекции
Построение цилиндра в изометрической проекции Построение графика функции
Построение графика функции Ряд Тейлора функции многих переменных. Лекция 19
Ряд Тейлора функции многих переменных. Лекция 19 Презентация на тему Решение задач В10 (ЕГЭ 2012)
Презентация на тему Решение задач В10 (ЕГЭ 2012)  Преобразование рациональных выражений
Преобразование рациональных выражений Биматричные игры
Биматричные игры Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Математическая игра Счастливое число 7!
Математическая игра Счастливое число 7!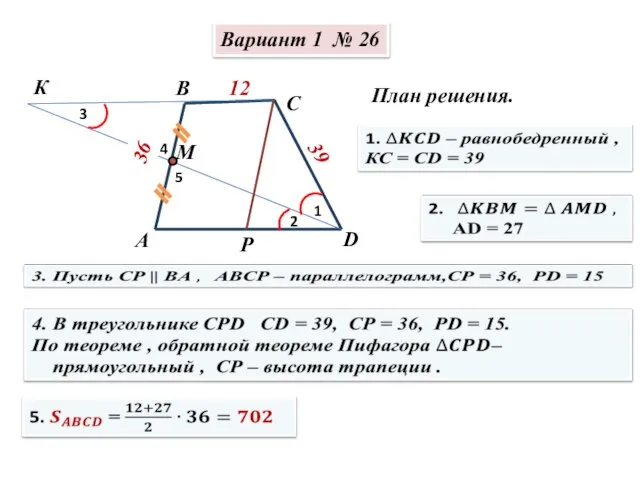 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Сложение и вычитание. Закрепление. Урок математики, 1 класс
Сложение и вычитание. Закрепление. Урок математики, 1 класс Сравнение множеств. Отображения множеств
Сравнение множеств. Отображения множеств Луч. Отрезок. Путешествие точки
Луч. Отрезок. Путешествие точки Презентация на тему Биссектриса угла в треугольнике
Презентация на тему Биссектриса угла в треугольнике  08_ ОТС_ Основы теории СП-2
08_ ОТС_ Основы теории СП-2 Сложение и вычитание многочленов
Сложение и вычитание многочленов Чётность и нечётность, периодичность тригонометрических функций с изменениями
Чётность и нечётность, периодичность тригонометрических функций с изменениями Случаи вычитания 17 -
Случаи вычитания 17 - Интерактивный тест Степень. Свойства степени
Интерактивный тест Степень. Свойства степени Модели пирамид
Модели пирамид Математика задача. Решение задачи уч. Стр.92 №2
Математика задача. Решение задачи уч. Стр.92 №2 Математика в профессии повара
Математика в профессии повара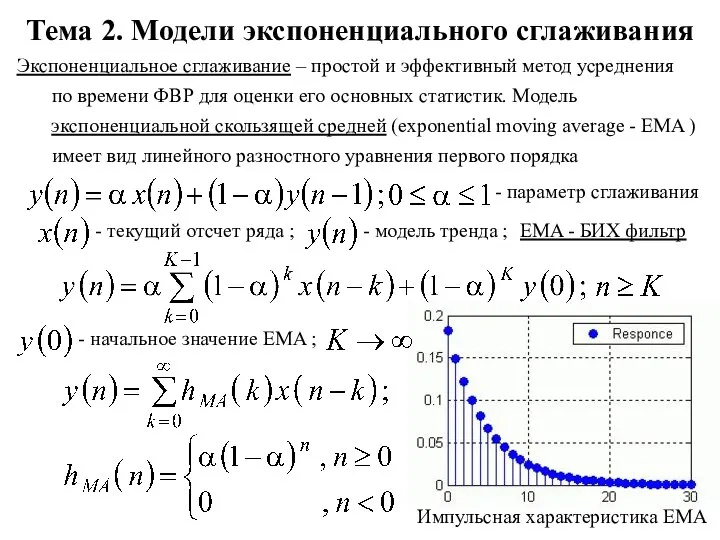 Модели экспоненциального сглаживания. Тема 2
Модели экспоненциального сглаживания. Тема 2 Презентация на тему Касательная к графику функции
Презентация на тему Касательная к графику функции  Треугольник. Виды треугольников
Треугольник. Виды треугольников