Радианная мера угла. Синус, косинус, тангенс числа

Тригономе́трия (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять),
то есть измерение треугольников) — раздел математики,
в котором изучаются тригонометрические функции и их приложения к геометрии.
Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (Bartholomäus Pitiscus, 1561—1613),
а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.

Эти ученые внесли свой вклад в развитие тригонометрии
Архимед
Фалес
Жозеф Луи
Лагранж

Тригонометрия возникла и развивалась в древности как один из разделов астрономии, как ее вычислительный аппарат, отвечающий практическим нуждам человека. С ее помощью можно определить расстояние до недоступных предметов и существенно упрощать процесс геодезической съемки местности для составления географических карт. Общепринятые понятия тригонометрии, а также обозначения и определения тригонометрических функция сформировались в процессе долгого исторического развития. Тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции встречающиеся уже в III веке до н.э.
в работах великих математиков– Евклида, Архимеда, Апполония Пергского. Древнегреческие астрономы успешно решали вопросы из тригонометрии, связанные с астрономией.

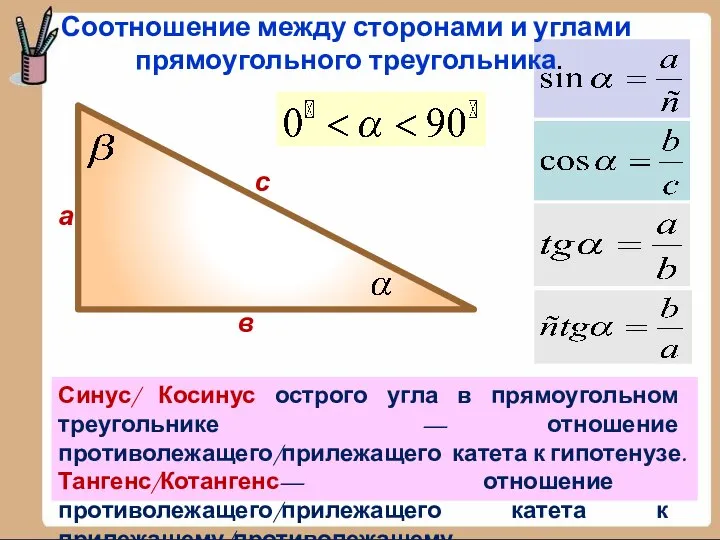
а
в
с
Синус/ Косинус острого угла в прямоугольном треугольнике — отношение противолежащего/прилежащего катета к гипотенузе.
Тангенс/Котангенс— отношение противолежащего/прилежащего катета к прилежащему/противолежащему.
Соотношение между сторонами и углами
прямоугольного треугольника

В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось.

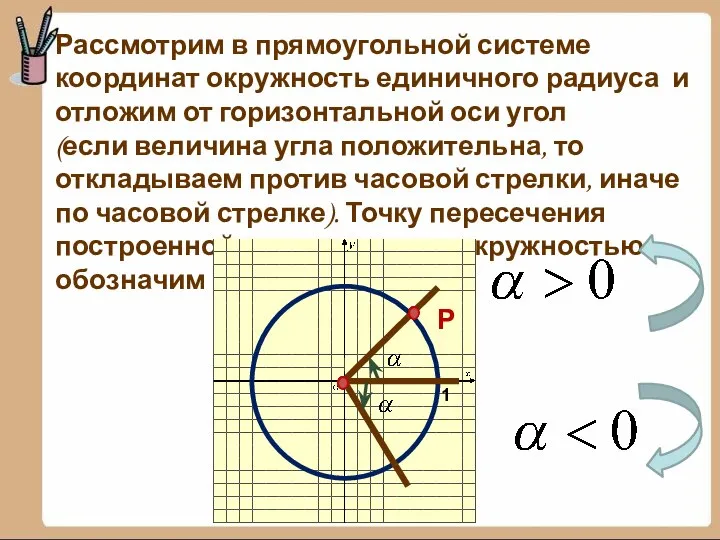
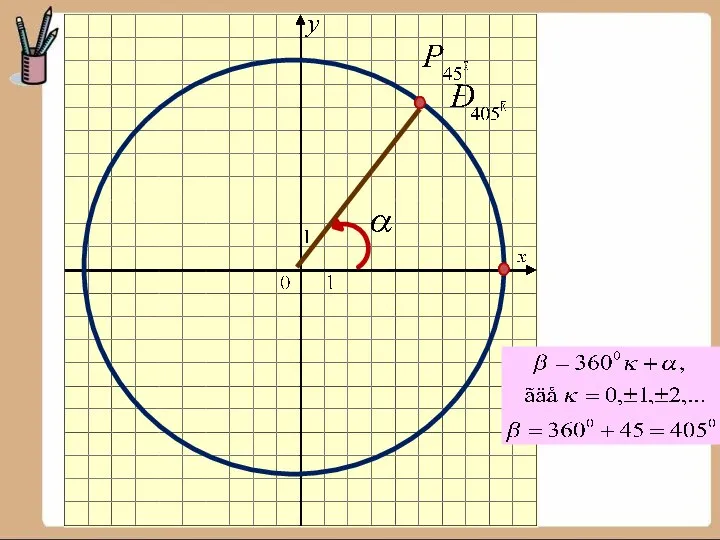
Рассмотрим в прямоугольной системе координат окружность единичного радиуса и отложим от горизонтальной оси угол
(если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим Р.
1
Р

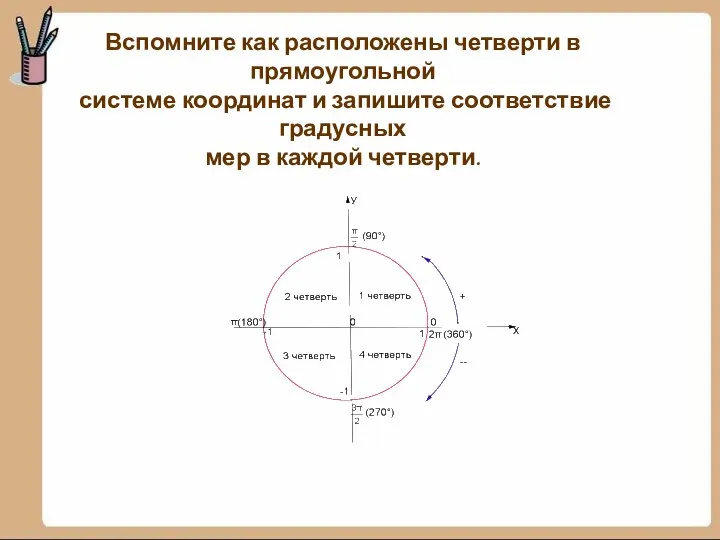
Вспомните как расположены четверти в прямоугольной
системе координат и запишите соответствие градусных мер в каждой четверти.

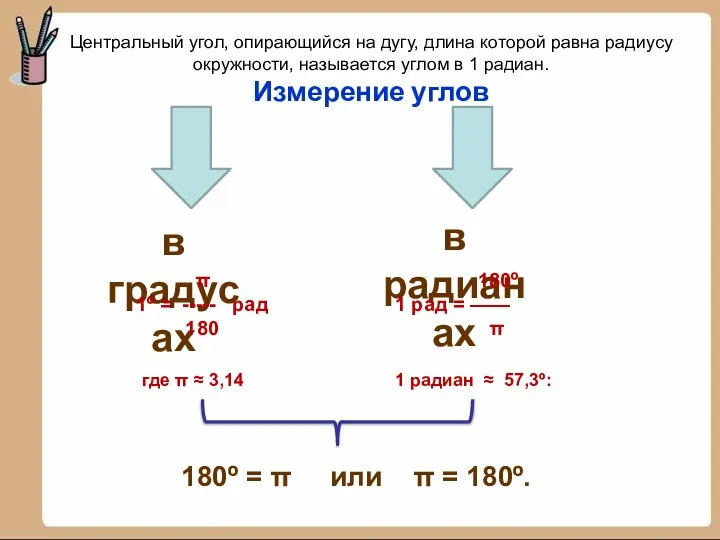
Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.
Измерение углов
в градусах
в радианах
π
1º = ----- рад
180
180º
1 рад = ——
π
1 радиан ≈ 57,3º:
где π ≈ 3,14
180º = π или π = 180º.

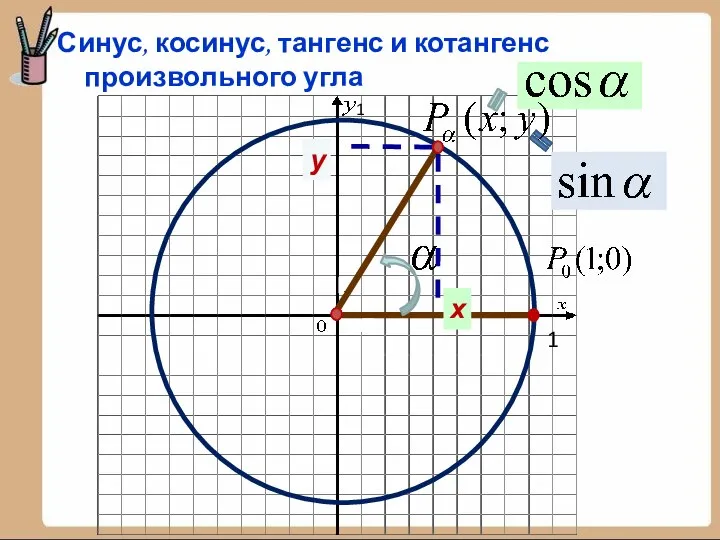
х
у
1
1
Синус, косинус, тангенс и котангенс произвольного угла

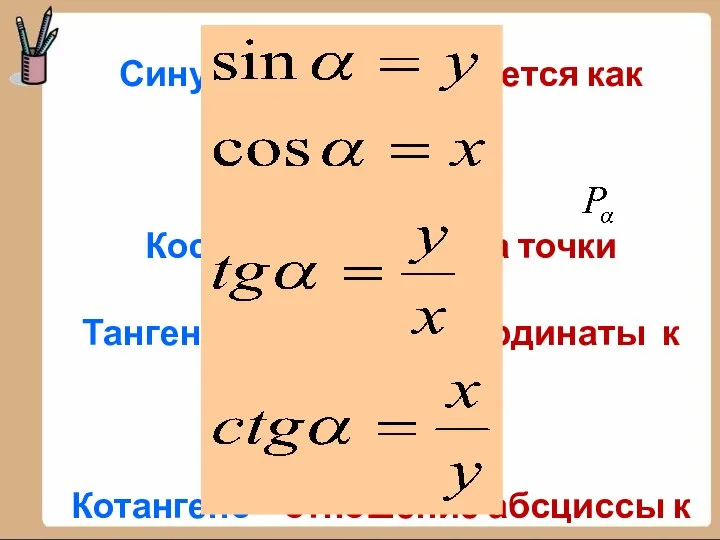
Синус угла определяется как ордината
точки
Косинус — абсцисса точки
Тангенс – отношение ординаты к абсциссе
точки
Котангенс – отношение абсциссы к ординате
точки

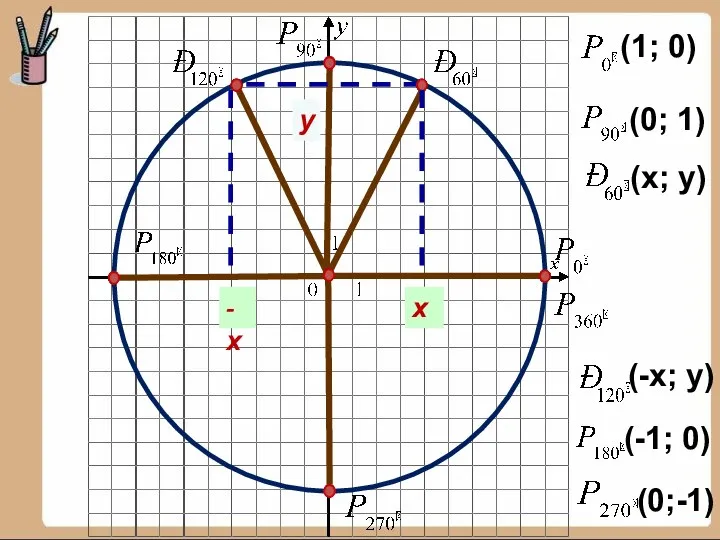
(1; 0)
(0; 1)
(-1; 0)
(0;-1)
-х
у
х
(x; y)
(-x; y)

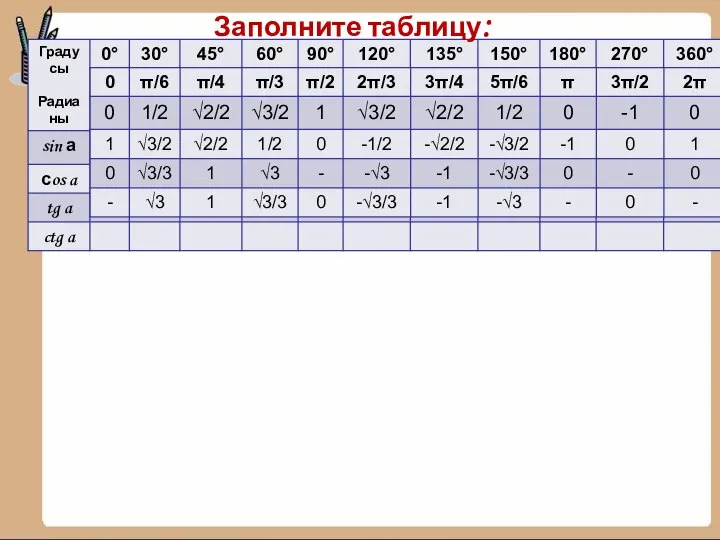
Заполните таблицу:

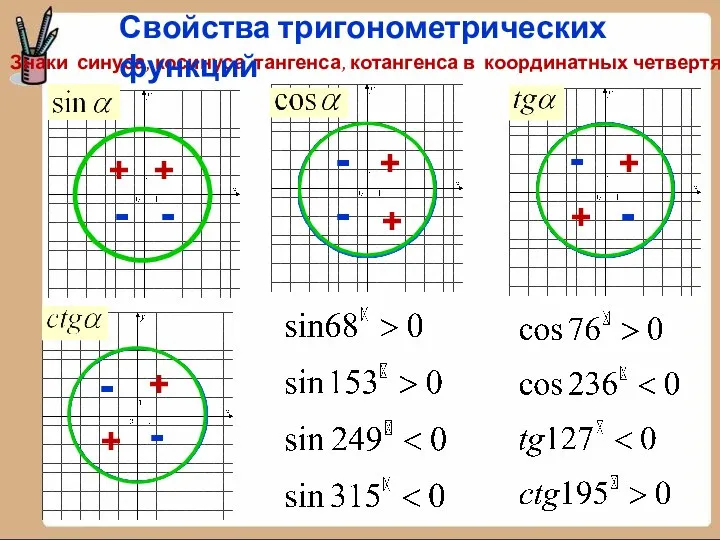
Знаки синуса, косинуса, тангенса, котангенса в координатных четвертях
+
+
+
+
+
+
+
+
-
-
-
-
-
-
-
-
Свойства тригонометрических функций

Четность, нечетность синуса, косинуса, тангенса, котангенса
Нечетные функции
Четная функция

Периодичность тригонометрических функций
При изменении угла на целое число оборотов
значения синуса, косинуса, тангенса, котангенса
не изменяются

08.10.21 Тема: Радианная мера угла. Синус, косинус, тангенс числа.
Литература: Ш.А.Алимов, Ю.М.Колягин и др., Алгебра и начала анализа, 10-11 класс, 2016.
стр.117 §21: конспект, задачи 1 и 2, №407, 408;
стр.121 §22: стр.124 - конспект, задачи 1 и 2;
стр. 126 §23: конспект, задачи 1, 2, 3;
стр. 129 таблицу записать в справочник.
5. Выполненное задание сфотографировать, вставить изображение в WORD и переслать преподавателю в СДО Mооdl.