Содержание
- 2. Случайное явление – это явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый
- 3. Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.
- 4. Под «событием» в теории вероятностей понимается всякое явление, которое в результате опыта или испытания может произойти
- 5. ПРИМЕРЫ ОПЫТОВ сдача экзамена, наблюдение за дорожно-транспортными происшествиями, выстрел из винтовки, бросание игрального кубика, химический эксперимент,
- 6. СОБЫТИЕ ПРИМЕР. Бросаем шестигранный игральный кубик. Определим события: А {выпало четное число очков}; В {выпало число
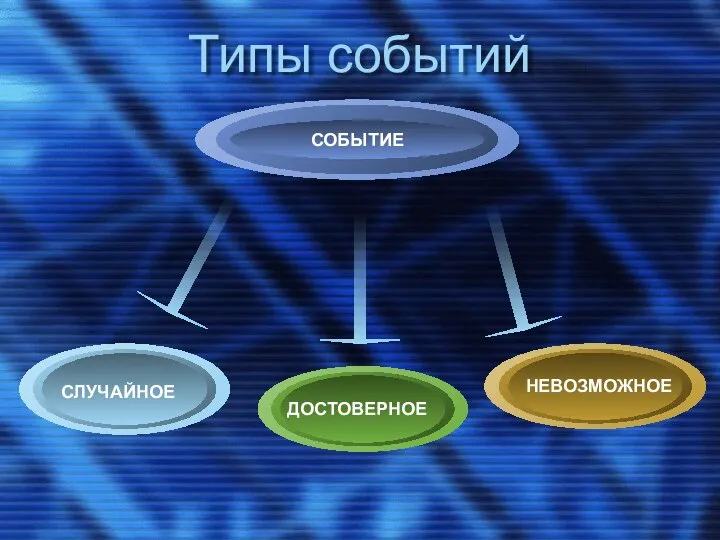
- 7. Типы событий ДОСТОВЕРНОЕ НЕВОЗМОЖНОЕ СЛУЧАЙНОЕ
- 8. СЛУЧАЙНОЕ СОБЫТИЕ СЛУЧАЙНЫМ называют событие, которое может произойти или не произойти в результате некоторого испытания (опыта).
- 9. ДОСТОВЕРНОЕ СОБЫТИЕ Достоверным называется событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий. Обозначают U.
- 10. НЕВОЗМОЖНОЕ СОБЫТИЕ Невозможным называется событие, которое заведомо не произойдет, если будет осуществлена совокупность условий. Обозначают V.
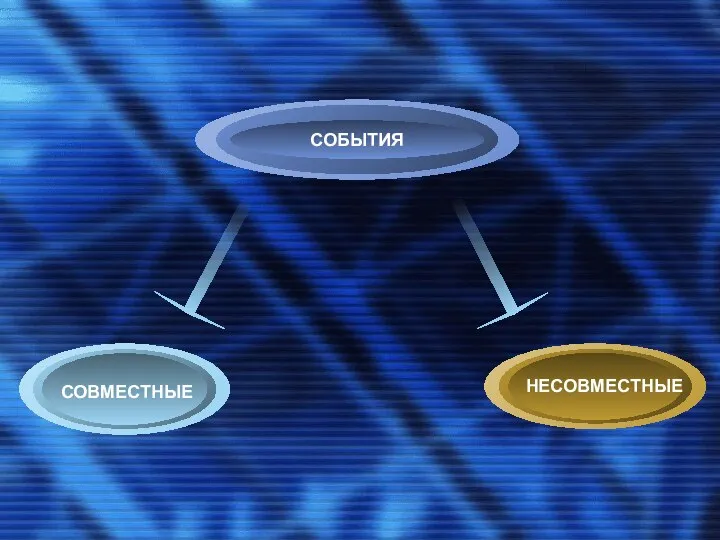
- 11. НЕСОВМЕСТНЫЕ СОВМЕСТНЫЕ
- 12. Два события А и В называют совместными, если они могут произойти одновременно, при одном исходе испытания,
- 13. Алгебраические операции над событиями Суммой двух событий А и В называется событие А или В (А
- 14. Вероятностью Р наступления случайного события А называется отношение , где n – число всех возможных исходов
- 15. Вероятность достоверного события равна 1: Р(U)=1 Вероятность невозможного события равна 0: P(V)=0 Вероятность случайного события А
- 16. Теоремы сложения и умножения вероятностей Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна
- 17. Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме
- 18. Теорема умножения вероятностей для независимых событий. вероятность совместного появления двух независимых событий равна произведению вероятностей этих
- 19. Теорема умножения вероятностей (зависимых) событий: Вероятность совместного появления двух событий равна произведению вероятности одного из них
- 20. Условной вероятностью РА (В) называют вероятность события В, вычисленную при условии, что событие А уже наступило.
- 22. Скачать презентацию

















 Признаки равенства треугольников
Признаки равенства треугольников Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Параллельность прямых и плоскостей (10 класс)
Параллельность прямых и плоскостей (10 класс) Умножение обыкновенных дробей
Умножение обыкновенных дробей TA&Ml_ukr_1
TA&Ml_ukr_1 Инженерно-вычислительные технологии
Инженерно-вычислительные технологии Применение производной к исследованию функции
Применение производной к исследованию функции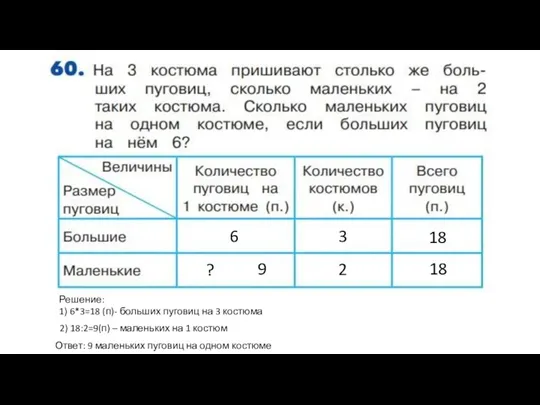 Задача о костюмах
Задача о костюмах Нахождение неизвестного вычитаемого
Нахождение неизвестного вычитаемого Дискретные случайные величины
Дискретные случайные величины Задание В11, открытого банка ЕГЭ по математике (часть 1)
Задание В11, открытого банка ЕГЭ по математике (часть 1) Критерий линейной корреляции Пирсона
Критерий линейной корреляции Пирсона Построение сечений
Построение сечений Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Решение уравнений сводящихся к линейным
Решение уравнений сводящихся к линейным Золотое сечение в архитектуре, скульптуре, живописи
Золотое сечение в архитектуре, скульптуре, живописи Задачи на построение
Задачи на построение Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)
Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)  Равносильные уравнения и неравенства
Равносильные уравнения и неравенства Компланарные векторы
Компланарные векторы Цветочное настроение (порядковый счет)
Цветочное настроение (порядковый счет) Венегрет. Урок
Венегрет. Урок Презентация по математике "Портреты учёных математиков" -
Презентация по математике "Портреты учёных математиков" -  График функций. Домашняя работа по алгебре
График функций. Домашняя работа по алгебре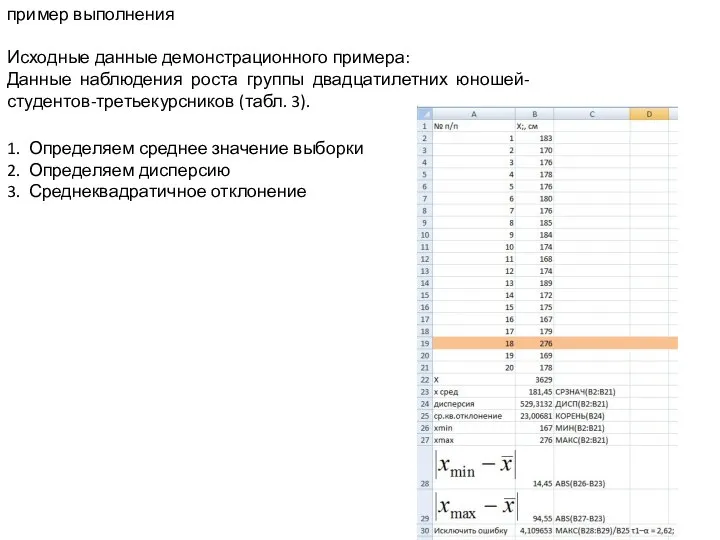 Данные наблюдения роста группы двадцатилетних юношей студентов
Данные наблюдения роста группы двадцатилетних юношей студентов Ломаная линия
Ломаная линия Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс