Слайд 2Решение тригонометрических уравнений в большинстве случаев проводится
либо с помощью замены переменной,

либо разложения на множители,
но тот и другой способ применяются в разных вариантах в зависимости от вида конкретного уравнения.
Поэтому вам предлагается более подробная классификация типов тригонометрических уравнений и методов их решения
Слайд 31. Замены с использованием основного тригонометрического тождества и формул косинуса двойного угла

Слайд 41. Замены с использованием основного тригонометрического тождества и формул косинуса двойного угла

Слайд 63. Метод дополнительного угла

Слайд 73. Метод дополнительного угла

Слайд 84.Преобразование суммы тригонометрических функций в произведение

Слайд 94.Преобразование суммы тригонометрических функций в произведение

Слайд 105.Преобразование произведения тригонометрических функций в сумму

Слайд 115.Преобразование произведения тригонометрических функций в сумму

Слайд 218.Уравнения,содержащие тангенс и котангенс

Слайд 228.Уравнения,содержащие тангенс и котангенс

Слайд 238.Уравнения,содержащие тангенс и котангенс

Слайд 2610. Иррациональные тригонометрические уравнения
При решении таких уравнений используются те же приемы,

что и при решении алгебраических иррациональных уравнений.
Особое внимание требуется обращать на дополнительные ограничения на допустимые значения переменной (самая распространённая ошибка в задачах такого типа-включение в ответ посторонних корней)
Слайд 2710. Иррациональные тригонометрические уравнения

Слайд 2810. Иррациональные тригонометрические уравнения

Слайд 2910. Иррациональные тригонометрические уравнения

Слайд 3011. Тригонометрические уравнения с модулем

Слайд 3111. Тригонометрические уравнения с модулем

Слайд 3212. Тригонометрические системы уравнений
Вновь перед нами комбинированные задачи, в которых применяются

известные из алгебры методы решения систем и способы решения тригонометрических уравнений.
Важно помнить, что при решении системы ответ каждого простейшего уравнения должен записываться с новым целочисленным параметром, который может принимать возможное значение независимо от ранее введенных параметров.
Слайд 3312. Тригонометрические системы уравнений

Слайд 3412. Тригонометрические системы уравнений

Слайд 3512. Тригонометрические системы уравнений



































 Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Решение задач. Самостоятельная работа (ЕГЭ)
Решение задач. Самостоятельная работа (ЕГЭ) Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве
Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве Метод координат на плоскости
Метод координат на плоскости Иррациональные уравнения. Задания для устного счета
Иррациональные уравнения. Задания для устного счета Устные упражнения. Выразите в процентах
Устные упражнения. Выразите в процентах Стереометрия. Метод координат в задачах ЕГЭ
Стереометрия. Метод координат в задачах ЕГЭ Задание 19. Профиль (1)
Задание 19. Профиль (1) Переменные величины и их свойства
Переменные величины и их свойства Линейная алгебра. (Матрицы, определители)
Линейная алгебра. (Матрицы, определители) Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена
Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена  Динамическое программирование
Динамическое программирование Задачи на нахождение неизвестного
Задачи на нахождение неизвестного Решаем задачу
Решаем задачу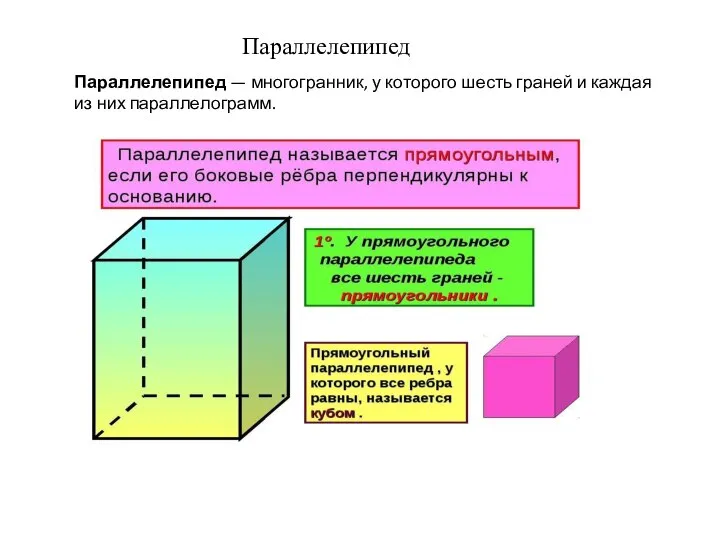 Параллелепипед
Параллелепипед Пирамида
Пирамида Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Число и цифра 6. 1 класс
Число и цифра 6. 1 класс Задания 15 и 4
Задания 15 и 4 Прямой угол
Прямой угол Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Функции, их свойства и графики
Функции, их свойства и графики Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Уравнение сферы
Уравнение сферы Геометрический и физический смысл производной
Геометрический и физический смысл производной Площадь параллелограмма
Площадь параллелограмма Изображение фигур в пространстве
Изображение фигур в пространстве