Векторная алгебра

http://e-library.kai.ru/dsweb/Get/Resource-1488/776493_0001.pdf
М. А. Дараган, С. И. Дорофеева
Практикум по векторной алгебре и аналитической геометрии
http://e-library.kai.ru/dsweb/Get/Resource-152/%D0%9C54.pdf
Э. М. Исхаков
Аналитическая геометрия и линейная алгебра

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.
БАЗИС И КООРДИНАТЫ.
Лекция №6

Основные определения
Его длина равна нулю, а направление для него не имеет смысла (не определено ).
НАЧАЛО
КОНЕЦ
НАЧАЛО
КОНЕЦ

Векторы, параллельные одной плоскости, называются КОМПЛАНАРНЫМИ.

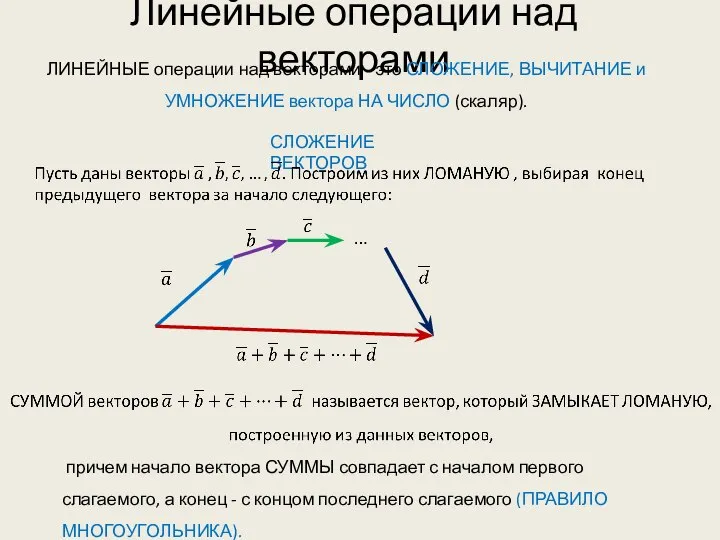
Линейные операции над векторами
ЛИНЕЙНЫЕ операции над векторами - это СЛОЖЕНИЕ, ВЫЧИТАНИЕ и
УМНОЖЕНИЕ вектора НА ЧИСЛО (скаляр).
СЛОЖЕНИЕ ВЕКТОРОВ
причем начало вектора СУММЫ совпадает с началом первого слагаемого, а конец - с концом последнего слагаемого (ПРАВИЛО МНОГОУГОЛЬНИКА).

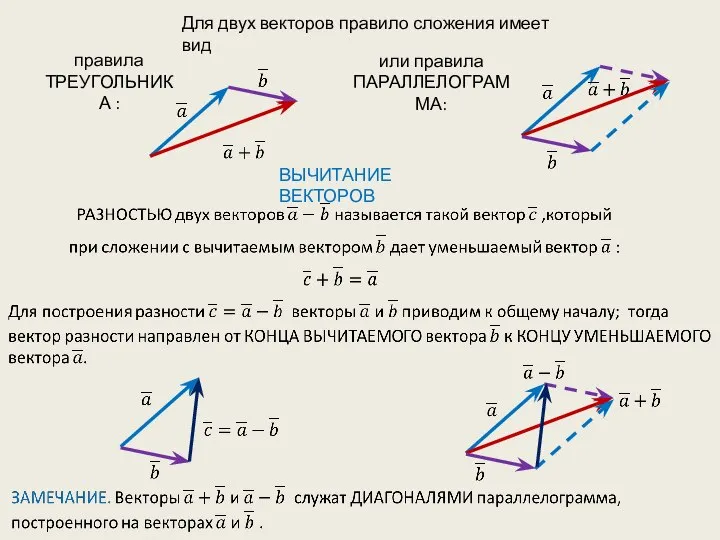
Для двух векторов правило сложения имеет вид
или правила
ПАРАЛЛЕЛОГРАММА:
ВЫЧИТАНИЕ ВЕКТОРОВ
правила
ТРЕУГОЛЬНИКА :

УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО

Условие коллинеарности двух векторов

Линейная зависимость и независимость векторов
Назовем линейную комбинацию ТРИВИАЛЬНОЙ , если ВСЕ коэффициенты в ней РАВНЫ НУЛЮ :
Если ЛЮБАЯ НЕТРИВИАЛЬНАЯ линейная комбинация векторов НЕ РАВНА НУЛЮ ,
то вектора называют ЛИНЕЙНО НЕЗАВИСИМЫМИ.
ТРИВИАЛЬНАЯ линейная комбинация любых векторов ВСЕГДА РАВНА НУЛЮ.
Если существует НЕТРИВИАЛЬНАЯ линейная комбинация , РАВНАЯ НУЛЮ , то вектора называют ЛИНЕЙНО ЗАВИСИМЫМИ:
Составим из них ЛИНЕЙНУЮ КОМБИНАЦИЮ (сумму произведений чисел и векторов ) :
( ПОЧЕМУ ?)

Критерий линейной зависимости
ДВА вектора ЛИНЕЙНО ЗАВИСИМЫ тогда и только тогда, когда они КОЛЛИНЕАРНЫ.
ТРИ вектора ЛИНЕЙНО ЗАВИСИМЫ тогда и только тогда, когда они КОМПЛАНАРНЫ.
Для трех векторов справедлива
ЧЕТЫРЕ вектора в пространстве всегда ЛИНЕЙНО ЗАВИСИМЫ.
ТЕОРЕМА 2.
ТЕОРЕМА 3.
линейная комбинация равна нулю, но она нетривиальна, так как
ЗАМЕЧАНИЕ.

Угол между векторами. Ось
векторами, приведенными к общему началу:
(ПОЧЕМУ? ОБЪЯСНИТЕ!)
ОСЬ - это прямая с выбранным положительным направлением.

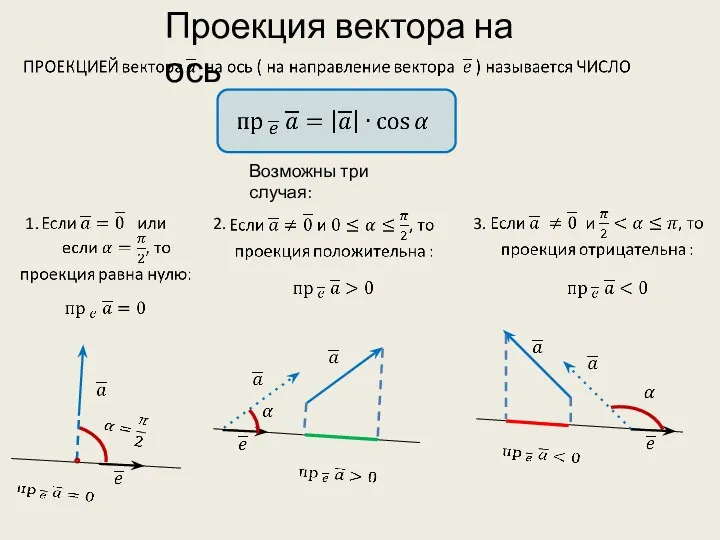
Проекция вектора на ось
Возможны три случая:
2.
3.
1.

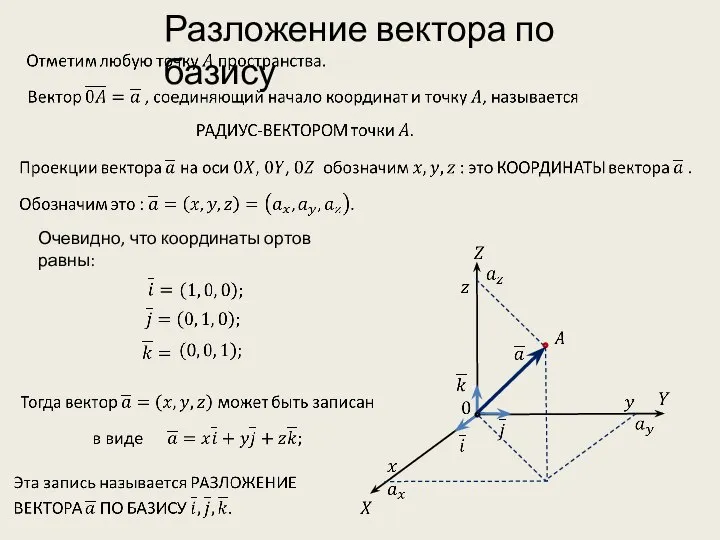
Прямоугольная система координат
Обозначим орты осей:
Зададим вектора в пространстве с помощью чисел.

Очевидно, что координаты ортов равны:
Разложение вектора по базису

Модуль вектора
извлекая корень из обеих частей равенства, получим :
МОДУЛЬ вектора равен КВАДРАТНОМУ КОРНЮ из СУММЫ КВАДРАТОВ его КООРДИНАТ, или проекций на оси.
РЕШЕНИЕ:
По теореме о длине диагонали прямоугольного параллелепипеда можно написать :

Направляющие косинусы вектора

Подставим выражение для проекций вектора в формулу модуля и получим :
Сократив на |ā|≠ 0, получим соотношение:
СУММА КВАДРАТОВ НАПРАВЛЯЮЩИХ КОСИНУСОВ ненулевого вектора РАВНА ЕДИНИЦЕ.
ВОПРОС : найти координаты орта е (единичного вектора), образующего с осями координат углы α, β, γ.
ОТВЕТ :
так как модуль орта равен единице, то
ex = |e| cosα ey = |e| cosβ ez = |e| cosγ
ex = cosα ey = cosβ ez = cosγ
e = (cosα; cosβ; cosγ)

Линейные операции в координатах
РАВЕНСТВО ВЕКТОРОВ
СЛОЖЕНИЕ и ВЫЧИТАНИЕ ВЕКТОРОВ
При СЛОЖЕНИИ векторов их одноименные координаты СКЛАДЫВАЮТСЯ;
При ВЫЧИТАНИИ векторов их одноименные координаты ВЫЧИТАЮТСЯ:
УМНОЖЕНИЕ на ЧИСЛО
При УМНОЖЕНИИ вектора на число КАЖДАЯ КООРДИНАТА УМНОЖАЕТСЯ на это ЧИСЛО :

Коллинеарность векторов
Вывод : ВЕКТОРА КОЛЛИНЕАРНЫ тогда и только тогда, когда их КООРДИНАТЫ ПРОПОРЦИОНАЛЬНЫ.
РЕШЕНИЕ :
Выясним условие коллинеарности векторов, заданных своими координатами.
В координатах это значит: