Слайд 2№ 1. Является ли решением неравенства 8x-12>3x+5 число
а) -3; б) 3;

в) 0; г) 5 ?
№ 2. Назовите два наименьших целых решения неравенства 15x+16>11x .
№ 3. Найдите наименьшее целое число, при котором двучлен 12x+36 принимает положительные значения.
№ 4. Назовите два наибольших целых решения неравенства -8x≥40 .
№ 5. Найдите количество целых положительных решений неравенства 5x-3≤27 .
Слайд 4Томас Гарриот
(1560 – 1621)
Усовершенствовал алгебраическую символику.
Ввёл знаки неравенств:
> (больше);
< (меньше) .

Слайд 5Пьер Бугер
(1698 – 1758)
Ввёл знаки неравенств
«не больше» и
«не меньше».

Слайд 6I ВАРИАНТ
№ 1. Решите неравенства:
а) 4x>12 ;
б) –x>11 ;
в) -x<0,3 ;
г) -4x≤24

;
д) 16x≤-0,32 .
Примечание. При решении неравенств учитывайте каким является числовой коэффициент при x , положительным или отрицательным числом.
Слайд 7№ 2. Решите неравенства:
а) 13d≤11d+7 ;
б) 4-b≥3+7b .
Примечание. Чтобы решить неравенства, нужно
перенести

члены, которые содержат переменную в левую часть, а свободные члены в правую часть неравенства;
привести подобные члены в каждой части неравенства;
3) разделить обе части неравенства на коэффициент при x, сохранить при этом знак неравенства, если этот коэффициент является числом положительным, и поменять знак неравенства, если этот коэффициент является отрицательным числом.






 Linear Algebra. Lecture 2
Linear Algebra. Lecture 2 Золотое сечение
Золотое сечение Первообразная и интеграл
Первообразная и интеграл Виды треугольников. Классификация треугольников по признаку длина сторон
Виды треугольников. Классификация треугольников по признаку длина сторон Презентация на тему Тригонометрические функции
Презентация на тему Тригонометрические функции  Волшебная страна математики: основы математики для детей 5-6 лет
Волшебная страна математики: основы математики для детей 5-6 лет Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график
Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график Корреляция. Показатель корреляции
Корреляция. Показатель корреляции Параллельность плоскостей
Параллельность плоскостей Возведение комплексных чисел в степень
Возведение комплексных чисел в степень Арифметико-логические устройства. Устройства управления
Арифметико-логические устройства. Устройства управления Виды и особенности нелинейных систем
Виды и особенности нелинейных систем Многомерные случайные величины
Многомерные случайные величины График функции. Тест
График функции. Тест Population statistical methods
Population statistical methods Неопределенный интеграл Ч2, свойства неопределенного интеграла
Неопределенный интеграл Ч2, свойства неопределенного интеграла Простейшие дифференциальные уравнения 2 порядка
Простейшие дифференциальные уравнения 2 порядка Презентация на тему Повторение курса начальной школы в 5-м классе
Презентация на тему Повторение курса начальной школы в 5-м классе  Интеллектуальная игра по математике: ТОК. Для учащихся 8-го класса
Интеллектуальная игра по математике: ТОК. Для учащихся 8-го класса Геометрический смысл дифференциала
Геометрический смысл дифференциала Скалярное произведение векторов. тест
Скалярное произведение векторов. тест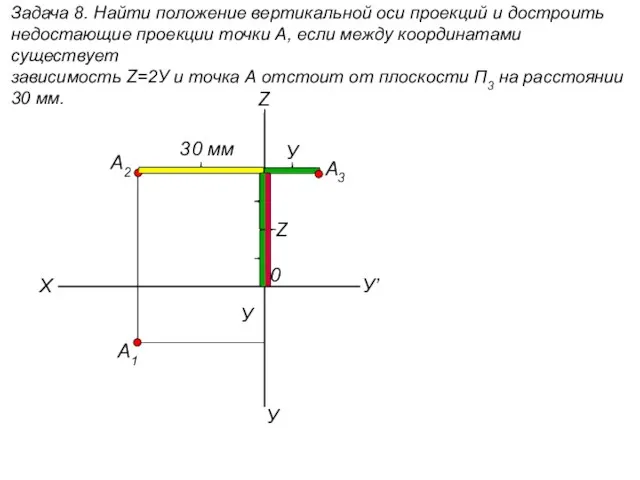 Найти положение вертикальной оси проекций и достроить недостающие проекции точки А. (задача 8)
Найти положение вертикальной оси проекций и достроить недостающие проекции точки А. (задача 8) Математическая игра Гусеница
Математическая игра Гусеница Дифференцирование функции
Дифференцирование функции Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Презентация на тему Признаки делимости
Презентация на тему Признаки делимости  Платоновы и Архимедовы тела
Платоновы и Архимедовы тела Циліндр. Елементи циліндра
Циліндр. Елементи циліндра