Содержание
- 2. ЧТО ТАКОЕ ЛОГАРИФМ Логари́фм числа b по основанию a (от др.-греч. λόγος, «отношение» + ἀριθμός «число»)
- 3. ИСТОРИЯ ЛОГАРИФМОВ История логарифмов как алгебраического понятия прослеживается с античных времён. Идейным источником и стимулом применения
- 4. В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов
- 5. ВИДЫ ЛОГАРИФМОВ Вещественный логарифм. Логарифм вещественного числа x=logab по определению есть решение уравнения ax=b. Случай a=1
- 6. Наиболее широкое применение нашли следующие виды логарифмов: Натуральные: loge b или ln b, основание: число Эйлера;
- 7. ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВО Из определения логарифма следует основное логарифмическое тождество. Следствие: из равенства двух вещественных логарифмов
- 8. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ аlogax = x, где a › 0, a ≠ 1. Если a › 1,
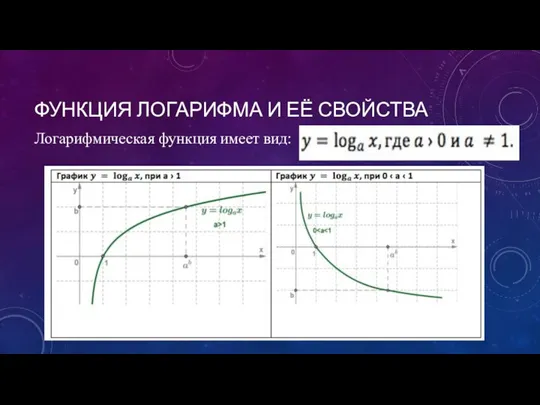
- 9. ФУНКЦИЯ ЛОГАРИФМА И ЕЁ СВОЙСТВА Логарифмическая функция имеет вид:
- 10. СВОЙСТВА область определения f(x) – множество всех положительных чисел, т.е. x может принимать любое значение из
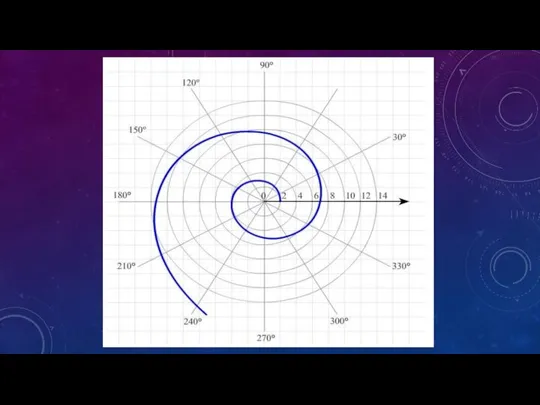
- 11. ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ Логарифмическая спираль представляет собой кривую, которую описывает точка, движущаяся вдоль луча, равномерно вращающегося вокруг
- 13. Поразительно, что в природе логарифмические спирали встречаются на каждом шагу. По логарифмической спирали растут раковины разнообразных
- 14. ЛОГАРИФМЫ В ПРОФЕССИИ "Т.О. И ОБСЛУЖИВАНИЕ АВТОМОБИЛЬНОГО ТРАНСПОРТА" В наше время нельзя представить экономику, Математику, Машиностроение,
- 15. ЛОГАРИФМ В АВТОМОБИЛЕ При разработки и проектировки любого автомобиля инженеры используют логарифмы для более точных расчетов
- 17. Скачать презентацию












 Сумма углов треугольника
Сумма углов треугольника Свойства степени с рациональным показателем
Свойства степени с рациональным показателем Производные функции нескольких переменных (часть 1)
Производные функции нескольких переменных (часть 1) Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3
Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3 Геометрия прически
Геометрия прически Сравнение множеств
Сравнение множеств Презентация на тему Уравнение множественной регрессии
Презентация на тему Уравнение множественной регрессии  Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Линейное уравнение с одной переменной. Подготовка к контрольной работе
Линейное уравнение с одной переменной. Подготовка к контрольной работе Прогрессии в физике
Прогрессии в физике Математические правила и законы
Математические правила и законы Признаки параллельности прямых
Признаки параллельности прямых Параллельность плоскостей
Параллельность плоскостей Мир функций и графиков. Урок - аукцион
Мир функций и графиков. Урок - аукцион Задачи на дроби (повторение)
Задачи на дроби (повторение) Координатная плоскость. Прямоугольная система координат
Координатная плоскость. Прямоугольная система координат Умножение и деление смешанных чисел
Умножение и деление смешанных чисел ОГЭ 2020-21. Задание №11. Прямая, гипербола, парабола
ОГЭ 2020-21. Задание №11. Прямая, гипербола, парабола 04.17.21.00[1]
04.17.21.00[1] Многогранники. Решение задач
Многогранники. Решение задач Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Анализ геометрических высказываний
Анализ геометрических высказываний Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости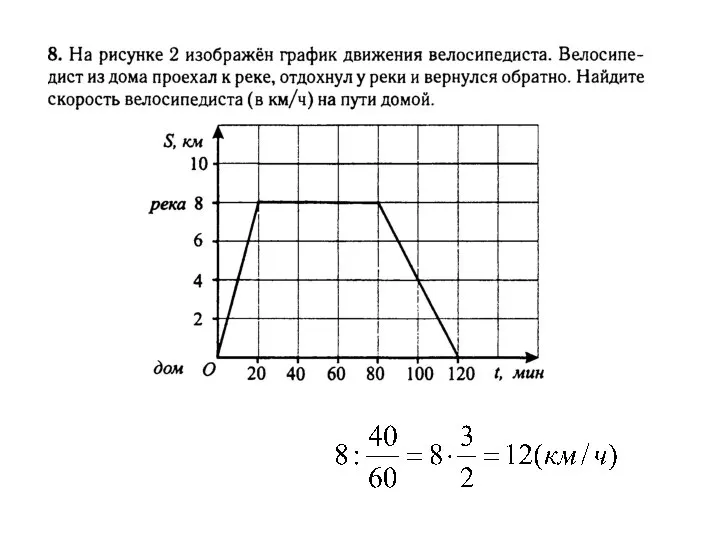 Линейная функция. Задания
Линейная функция. Задания Параллелограмм. Свойства параллелограмма. Трапеция
Параллелограмм. Свойства параллелограмма. Трапеция Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Метрология. Стандартизация
Метрология. Стандартизация Презентация на тему Квадратные уравнения 8 класс
Презентация на тему Квадратные уравнения 8 класс