Содержание
- 2. Содержание I. Понятие вектора в пространстве II. Коллинеарные векторы III. Компланарные векторы IV. Разложение вектора Выход
- 3. Признак коллинеарности Доказательство
- 4. Доказательство признака коллинеарности
- 5. Определение компланарных векторов Компланарные векторы – векторы, при откладывании которых от одной и той же точки
- 6. О компланарных векторах Любые два вектора всегда компланарны. Три вектора, среди которых имеются два коллинеарных, компланарны.
- 7. Признак компланарности Доказательство Задачи
- 8. Задачи на компланарность Компланарны ли векторы: а) б) Справка Решение Известно, что векторы , и компланарны.
- 9. Решение
- 10. Решение
- 11. Решение
- 12. Доказательство признака компланарности С O A1 B1 B A
- 13. Свойство компланарных векторов
- 14. Скалярное произведение Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. Справедливые
- 15. Справедливые утверждения скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны
- 16. Вычисление скалярного произведения в координатах Доказательство
- 17. Доказательство формулы скалярного произведения O A B α O B A O B A
- 18. Доказательство формулы скалярного произведения
- 19. Свойства скалярного произведения 10. 20. 30. 40. (переместительный закон) (распределительный закон) (сочетательный закон)
- 20. Разложение вектора По двум неколлинеарным векторам По трем некомпланарным векторам
- 21. Разложение вектора по двум неколлинеарным векторам Теорема. Любой вектор можно разложить по двум данным неколлинеарным векторам,
- 22. Доказательство теоремы O A A1 B P Пусть коллинеарен . Тогда , где y – некоторое
- 23. не коллинеарен ни вектору , ни вектору . Отметим О – произвольную точку. Доказательство теоремы
- 24. Доказательство теоремы Докажем, что коэффициенты разложения определяются единственным образом. Допустим: Тогда: -
- 25. Разложение вектора по трем некомпланарным векторам Если вектор p представлен в виде где x, y, z
- 26. Доказательство теоремы С O A B P1 P2 P
- 28. Скачать презентацию

























 Среднее арифметическое
Среднее арифметическое Основы моделирования
Основы моделирования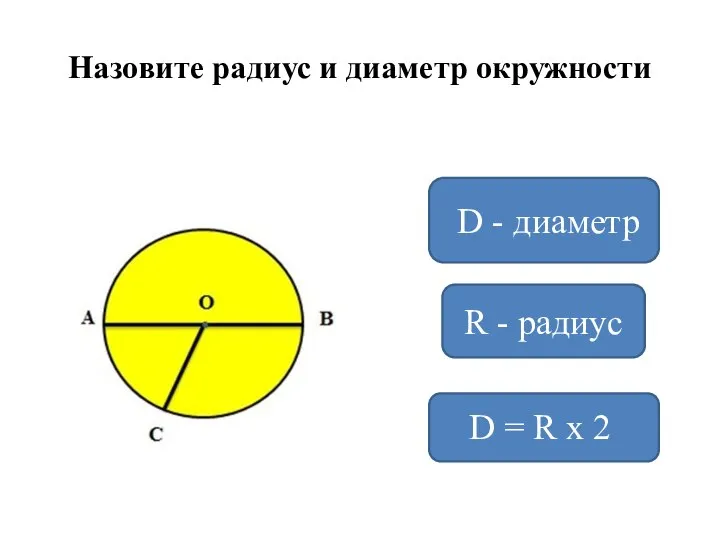 Радиус и диаметр окружности
Радиус и диаметр окружности Замечательные отрезки многоугольников
Замечательные отрезки многоугольников Площадь круга
Площадь круга Километр
Километр Презентация по математике "Знакомство с занимательной литературой по математике" -
Презентация по математике "Знакомство с занимательной литературой по математике" -  Неравенства с двумя переменными и их системы
Неравенства с двумя переменными и их системы Решение задач модуля Геометрия
Решение задач модуля Геометрия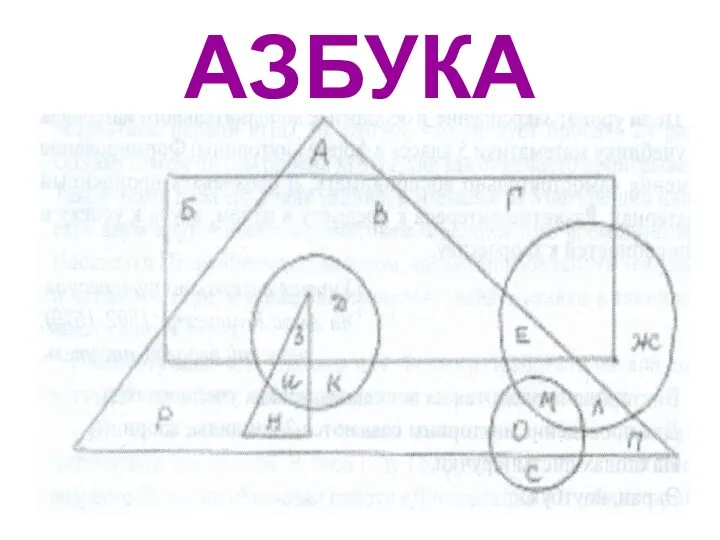 Азбука
Азбука Корни натуральной степени из числа, их свойства
Корни натуральной степени из числа, их свойства Площадь эллипса и окружности
Площадь эллипса и окружности Ringjoon, lõikaja, puutuja, kesk- ja piirdenurk. (8 klass)
Ringjoon, lõikaja, puutuja, kesk- ja piirdenurk. (8 klass) Математический диктант
Математический диктант Дидактическая игра. Веселый ёжик
Дидактическая игра. Веселый ёжик Трапеция. 8 класс
Трапеция. 8 класс Производные от неявных функций. Лекция 18
Производные от неявных функций. Лекция 18 Путешествие в страну Эколандию
Путешествие в страну Эколандию Презентация на тему Занимательные задачи (5 класс)
Презентация на тему Занимательные задачи (5 класс)  Перпендикулярность плоскостей
Перпендикулярность плоскостей Координатная плоскость
Координатная плоскость Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Подготовка к ЕГЭ (профильный уровень). Задания 5
Подготовка к ЕГЭ (профильный уровень). Задания 5 Проверка статистических гипотез. Критерий согласия Пирсона (хи-квадрат)
Проверка статистических гипотез. Критерий согласия Пирсона (хи-квадрат)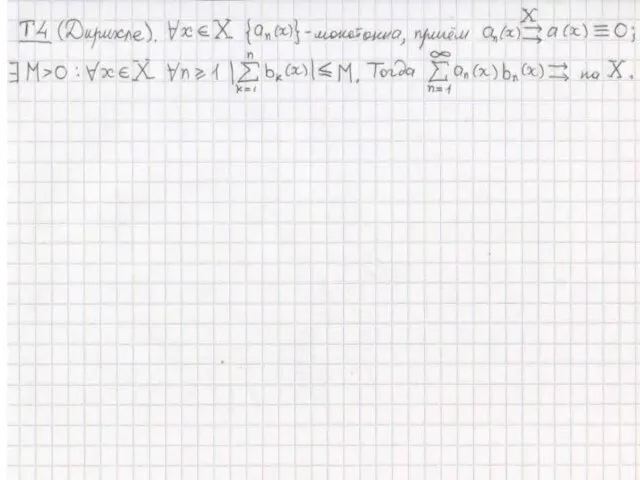 Свойства равномерно-сходящихся плоскостей и рядов
Свойства равномерно-сходящихся плоскостей и рядов Понятие числовой последованности
Понятие числовой последованности Diskretnaya_matematika-2 2
Diskretnaya_matematika-2 2 Простейшие задачи. Теоретический тест в координатах. 9 класс
Простейшие задачи. Теоретический тест в координатах. 9 класс