Статистическая проверка гипотез

Учебный вопрос
Статистическая проверка гипотез

ПОДВОПРОС
Основные понятия статистической проверки гипотез.

Статистической гипотезой называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.
Примеры статистических гипотез:
генеральная совокупность распределена по нормальному закону;
генеральная совокупность распределена по закону Пуассона.

Приведем примеры задач, которые могут быть решены с помощью проверки статистических гипотез:
1. Используется два метода измерения одной и той же величины. Первый метод дает оценки этой величины, второй - . Требуется определить, обеспечивают ли два метода измерения одной и той же величины одинаковую точность измерений.

2. Контроль точности работы некоторой производственной системы. Получаемые характеристики выпускаемой продукции характеризуются некоторым разбросом (дисперсией). Обычно величина этого разброса не должна превышать некоторого заранее заданного уровня. Требуется определить, обеспечивает ли система (например, линия сборки или отдельный станок) заданную точность.

Нулевой гипотезой (основной) называют выдвинутую гипотезу . Основная гипотеза H0 — это то утверждение, которое подлежит проверке.
Наряду с выдвинутой гипотезой всегда рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то принимается противоречащая гипотеза.

Альтернативной гипотезой (конкурирующей) H1 называют гипотезу , которая противоречит нулевой.
Например, если нулевая гипотеза состоит в предположении, что математическое ожидание нормального распределения равно 5, то альтернативная гипотеза, например, может состоять в предположении, что не равна 5.

Из генеральной совокупности проводят выборку объе­ма n.
Для этой выборки вычисляют нужные характеристики.
Формулируют две гипотезы: основную H0 и альтер­нативную H1.
Простой называют гипотезу, содержащую только одно предположение.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки.

В итоге статистической проверки гипотезы в двух случаях может быть
принято неправильное решение, т.е. могут быть допущены ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Если, например, принят уровень значимости 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу).
Очень часто генеральная совокупность должна подчи­няться некоторым параметрам. Например, фасовочная машина должна наполнять пакеты сахаром по 1 кг. Как уз­нать, действительно ли генеральная совокупность подчи­няется этим ограничениям? C этой целью проводят испытания гипотез.

По результатам выборки вычисляется величина, называемая статистикой. Формула для вычисления статистики зависит от вида решаемой задачи. Значение статисти­ки наносят на координатную ось.

B зависимости от взаимного расположения значения статистики и граничных точек возможен один из трех вариантов:
нет оснований отвергнуть гипотезу H0;
отклоняется гипотеза H0 ( без всякой проверки принимается H1 );
доказательство является неубедительным, нужно боль­ше данных.

Опрос по учебному вопросу
Определение нулевой статистической гипотезы.
Определение альтернативной статистической гипотезы.
Определение доверительной вероятности (надежности). Ее обозначение?
Определение уровня значимости. Ее обозначение? Каким его принимают?

ПОДВОПРОС.
Критерий Пирсона
χи-квадрат. Примеры задач.

Критерий χ² применяется для определения связи между качественными признаками. Также его можно применять для определения сходства эмпирических распределений или для проверки гипотезы о совпадении эмпирического распределения с предсказанным теоретическим. Например, с помощью критерия χ² можно определить вероятность совпадения эмпирического распределения с нормальным. Обычно χ² используется, когда количество измерений больше или равно 40.

Для определения количества интервалов (карманов) можно использовать следующее правило:
Если количество измерений n:
от 40 до 100, то рекомендуется выбрать от 7 до 9 интервалов;
от 100 до 500, то рекомендуется выбрать от 8 до 12 интервалов;
от 500 до 1000, то рекомендуется выбрать от 10 до 16 интервалов;
1000 – 10000, то рекомендуется выбрать от 12 до 22 интервалов.

Если есть интервалы с частотами менее 5, то их необходимо объединить с соседними интервалами.
Величины интервалов классов при этом подлежат пересчету, переопределяются границы классов от xi до xi+1 .

Параметры нормального распределения для расчета теоретических вероятностей вычисляются по эмпирическим частотам, т.к. мы не знаем истинных параметров генеральной совокупности.

Пример . Проводилось экспериментальное исследование по изучению влияния развлекательной телепередачи на молодежь. Испытуемые пожелавшие принять участие в исследовании случайным образом были разделены на две группы экспериментальную (теоретическую)и контрольную. Одним из параметров оценки влияния телепередачи служил показатель личностной тревожности. Результаты испытуемых контрольной и экспериментальной группы даны в таблице .

Вопрос: Можно ли утверждать, что полученные эмпирические данные подчиняются закону нормального распределения?

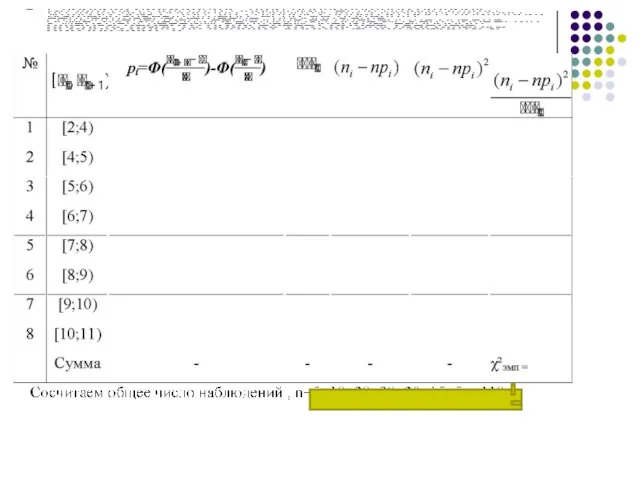
Разобьем данные на классы, частота которых себя не менее пяти измерений, для этого нам придется объединить испытуемых набравших 2 и 4 балла в один класс (в первый).
Перепишем таблицу, указав интервалы классов.

Так в интервал от [2;4)у нас попадает 2+4=6 испытуемых.
В интервал от [ 4 ; 5) попадает 10 испытуемых.
И т.д. Проблемы возникают только с последним интервалом, а значит необходимо добавить интервал [ 10 ; 11) .
На частоту попадания испытуемых в этот интервал это никак не скажется.

До обьединения было 9 классов;