Содержание
- 2. Ряды динамики (временные ряды) применяются для изучения изменения явлений во времени. Ряд динамики представляет собой ряд
- 3. РЯД ДИНАМИКИ последовательность изменяющихся во времени значений статистического показателя , расположенного в хронологическом порядке
- 4. Составными элементами ряда динамики являются показатели уровней ряда и периоды времени (годы , кварталы , сутки)
- 5. Пример Здесь t – время; yi – производство продукции, тыс. шт.
- 6. В зависимости от способа выражения уровней ряда ряды динамики делятся на ряды :
- 7. В зависимости от того , как выражают уровни ряда (на начало месяца или за период),выделяют моментные
- 8. Ряды динамики подразделяются на моментные и интервальные. Моментным называется ряд, абсолютные уровни которого характеризуют величину явления
- 9. Интервальным называется такой ряд, абсолютные уровни которого представляют собой итоговые величины за некоторые интервалы времени (например,
- 10. Выделяют также производные ряды динамики, которые состоят из средних или относительных величин. Они рассчитываются на основе
- 11. Основные показатели, применяемые для анализа рядов динамики
- 12. Анализ скорости и интенсивности явления во времени осуществляется с помощью статистических показателей , которые получаются в
- 13. Различают показатели изменения уровней ряда и средние характеристики рядов динамики
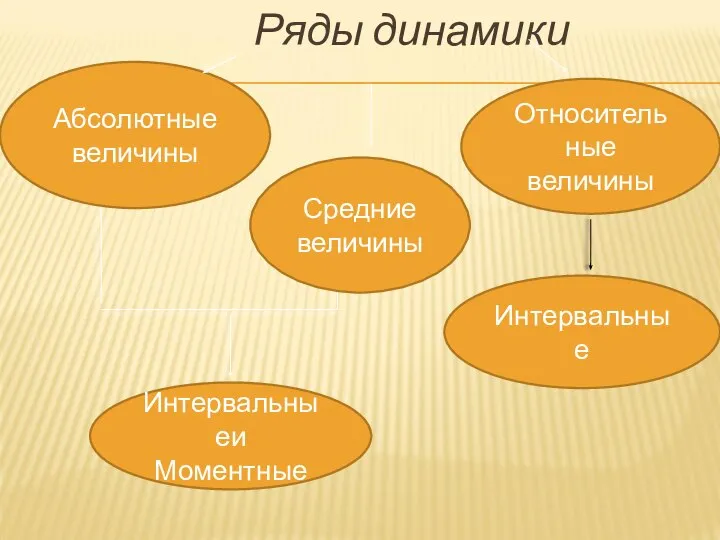
- 14. Средние величины Ряды динамики Абсолютные величины Относительные величины Интервальныеи Моментные Интервальные
- 15. К показателям изменения уровней ряда относятся абсолютный прирост, коэффициент роста и прироста, темп роста и прироста,
- 16. 1.Абсолютные приросты бывают цепными и базисными. Абсолютный прирост показывает, на сколько изменился изучаемый показатель по сравнению
- 17. Базисный абсолютный прирост: где - базисный уровень ряда
- 18. Цепной абсолютный прирост: где - текущий уровень ряда; - предыдущий уровень ряда
- 20. 2. Коэффициент роста показывает, во сколько раз изменился изучаемый показатель по сравнению с предыдущим периодом времени
- 21. Цепной коэффициент роста:
- 22. Базисный коэффициент роста:
- 23. 3.Темпы роста – это коэффициенты роста, выраженные в процентах (они также могут быть цепными, базисными и
- 24. Темп роста: а) базисный: б) цепной :
- 25. 4.Темп прироста используется для выражения величины абсолютного прироста уровней ряда динамики в относительных величинах:
- 26. Темп прироста показывает, на сколько процентов изменился изучаемый показатель по сравнению с предыдущим периодом времени или
- 27. Базисный темп прироста
- 28. 5.Абсолютное значение одного процента прироста А% показывает, сколько абсолютных единиц содержится в 1% прироста
- 29. Содержание одного процента базисного прироста:
- 30. Содержание одного процента цепного прироста:
- 32. Расчет среднего уровня ряда динамики
- 33. СРЕДНИЕ ХАРАКТЕРИСТИКИ РЯДА Средний уровень ряда динамики рассчитывается по формулам средней арифметической или средней хронологической
- 34. 1.Если ряд динамики является интервальным, то расчет среднего уровня ведется по формуле простой средней арифметической:
- 35. СРЕДНИЙ УРОВЕНЬ РЯДА ДЛЯ ИНТЕРВАЛЬНЫХ РЯДОВ С РАВНЫМИ ИНТЕРВАЛАМИ ВРЕМЕНИ Простая средняя арифметическая = где n
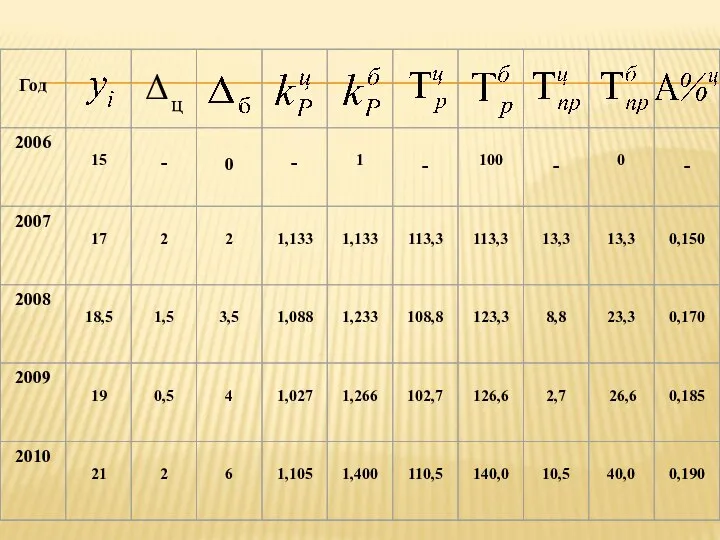
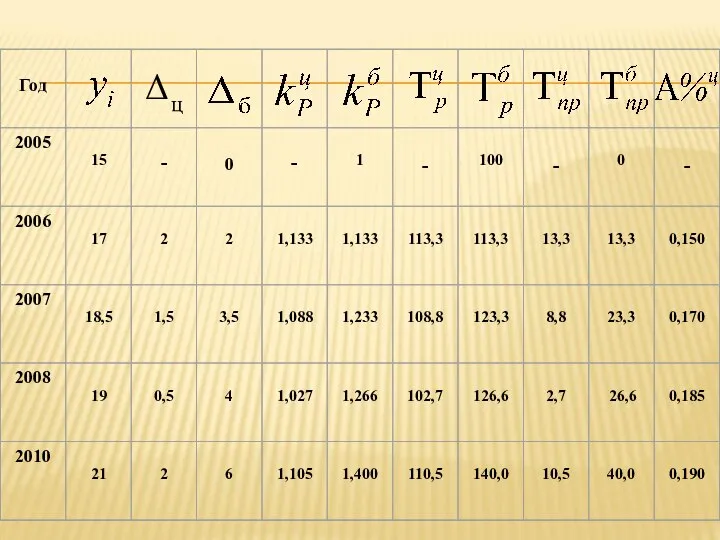
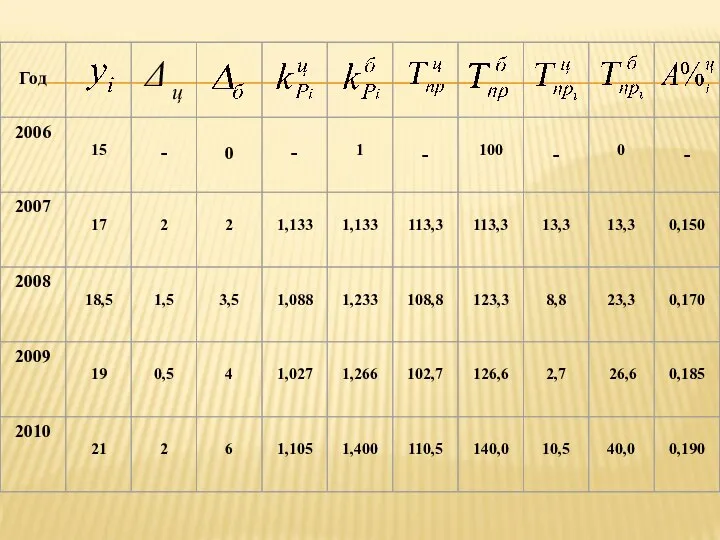
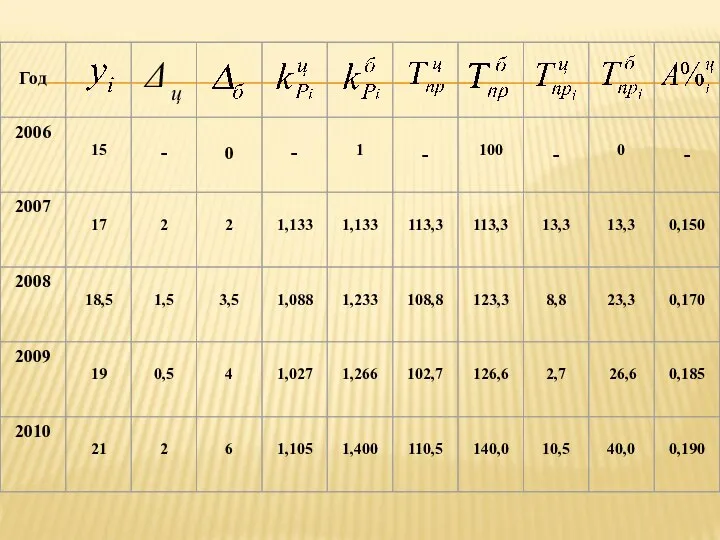
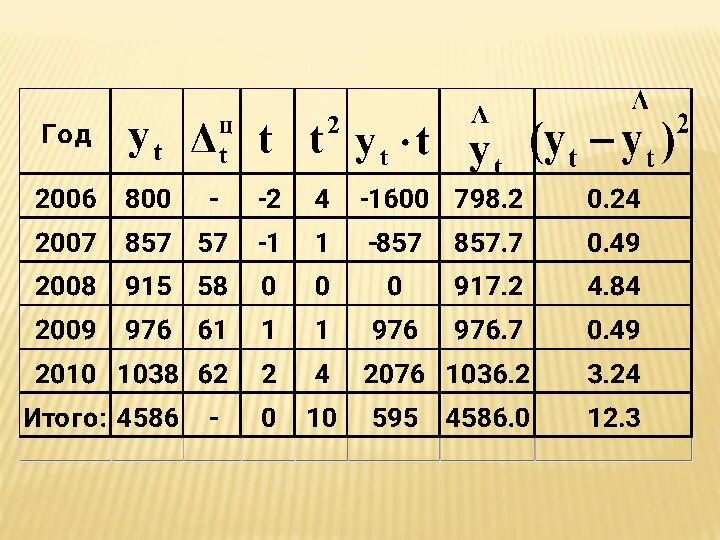
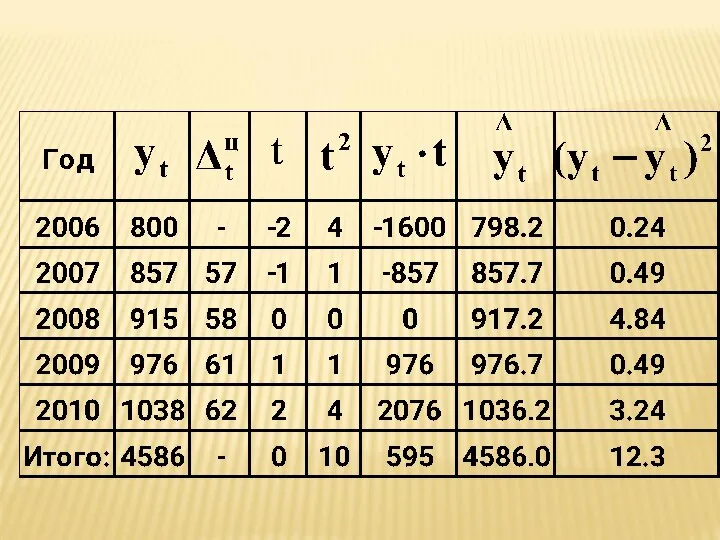
- 36. Пример. Имеются следующие данные о динамике производства продукции предприятием за 2006-2010 гг., тыс. шт. Определить среднегодовое
- 37. 2. Если ряд динамики является моментным с различными интервалами времени между датами, то для расчета среднего
- 38. Пример. Известна списочная численность персонала организации по состоянию на следующие даты (человек) : Среднесписочная численность персонала
- 39. С неравными интервалами времени Эта формула иногда дается как взвешенная средняя хронологическая = где ti –
- 40. 3.Если ряд динамики является моментным с равноотстоящими уровнями, то используется средняя хронологическая простая: где n-количество дат
- 41. Пример. Известны товарные остатки магазина на 1-е число каждого месяца (тыс. руб.) : Средний уровень товарных
- 42. Средний абсолютный прирост определяется как простая средняя арифметическая величина из цепных абсолютных приростов и показывает ,
- 43. Средний абсолютный прирост показывает, на сколько в среднем изменялся изучаемый показатель при переходе от предыдущего периода
- 46. Среднегодовой коэффициент роста определяется как средняя геометрическая из цепных коэффициентов роста и показывает , сколько в
- 47. Если цепные коэффициенты роста определялись для рядов с равностоящими интервалами, то применяется простая средняя геометрическая величина
- 48. Средний коэффициент роста рассчитывается по формуле средней геометрической из цепных коэффициентов роста:
- 51. С неравными интервалами времени Взвешенная средняя геометрическая = где ki – коэффицент роста; ti – период
- 52. Среднегодовой темп роста определяется умножением среднегодового коэффициента роста на 100 и показывает , сколько процентов в
- 53. СРЕДНИЙ ТЕМП ПРИРОСТА Показывает, на сколько процентов увеличивается (или уменьшается) уровень по сравнению с предыдущем в
- 55. Проблема сопоставимости уровней рядов динамики Смыкание рядов динамики
- 56. Поскольку ряды динамики формируются на протяжении длительных периодов времени, их уровни часто оказываются несопоставимыми
- 57. Причины Изменение цен Изменение методики расчета показателей Изменение «границ» (организа- ционных, административных)
- 58. Для обеспечения сопоставимости данных часто применяется метод смыкания рядов динамики. Для смыкания ряда динамики необходимо иметь
- 63. Анализ основной тенденции рядов динамики
- 64. Уровни рядов динамики формируются под воздействием большого числа факторов. Их можно разделить на 3 группы
- 65. 1. Определяющие факторы – факторы, которые оказывают постоянное и сильное воздействие на изучаемый показатель. Они определяют
- 67. 2. Сезонные факторы – факторы, которые вызывают сезонные колебания относительно основной тенденции
- 69. 3. Случайные факторы – факторы, которые вызывают случайные колебания уровней ряда (например, погодный фактор)
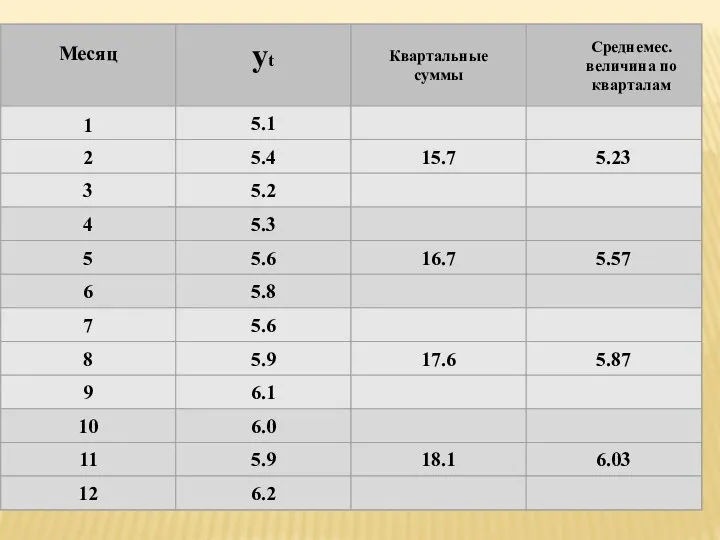
- 70. Метод укрупнения интервалов
- 71. Метод укрупнения интервалов – замена исходных уровней ряда средними величинами, которые рассчитываются для укрупненных интервалов
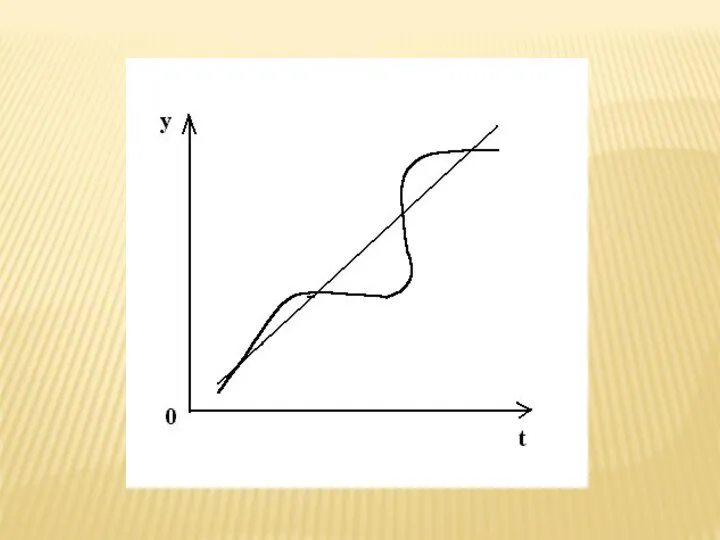
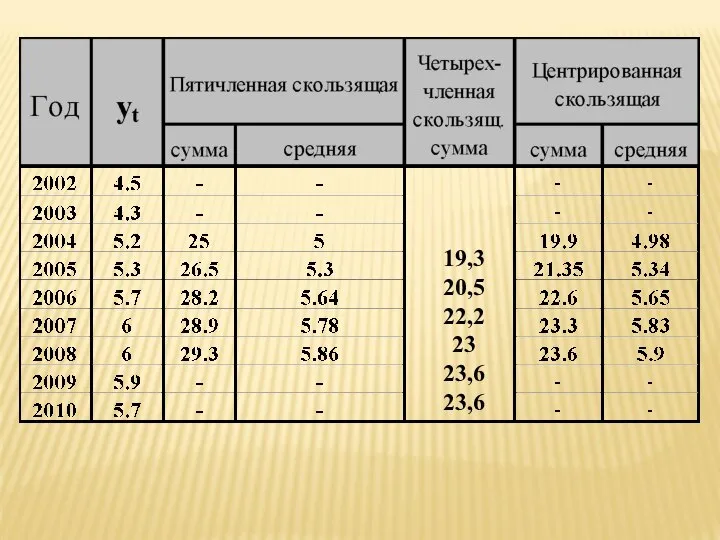
- 73. Метод скользящей средней
- 74. Метод скользящей средней– замена исходных уровней ряда средними величинами, которые рассчитываются для последовательно смещающихся интервалов времени
- 75. 19,3 20,5 22,2 23 23,6 23,6
- 76. Аналитическое выравнивание рядов динамики
- 77. Уровни ряда рассматриваются как некоторая функция от времени:
- 78. Процедура выравнивания в этом случае сводится: ⮚ к выбору вида функции; ⮚ к определению параметров функции;
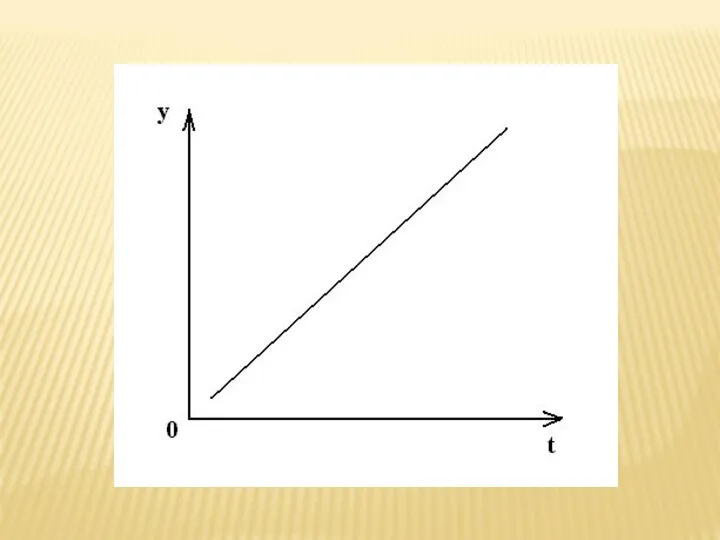
- 79. Рассмотрим данный метод на примере линейного уравнения (тренда): где a и b – параметры; t –
- 80. Линейный тренд лучше всего использовать в тех случаях, когда предварительный анализ показывает, что уровни ряда изменяются
- 81. Параметры a и b определяются при помощи метода наименьших квадратов (МНК)
- 82. Применение метода МНК дает следующую систему уравнений для определения параметров:
- 83. Данную систему уравнений можно существенно упростить, если пронумеровать время таким образом, чтобы
- 84. Если ряд содержит нечетное число уровней, то центральный уровень ряда нумеруется нулем. Уровни в сторону убывания
- 85. Если ряд содержит четное число уровней, то ближайшие к центру уровни ряда нумеруются: -1 и 1,
- 90. Выравнивание по параболе второго порядка: где b – скорость изменения уровней ряда динамики c – ускорение
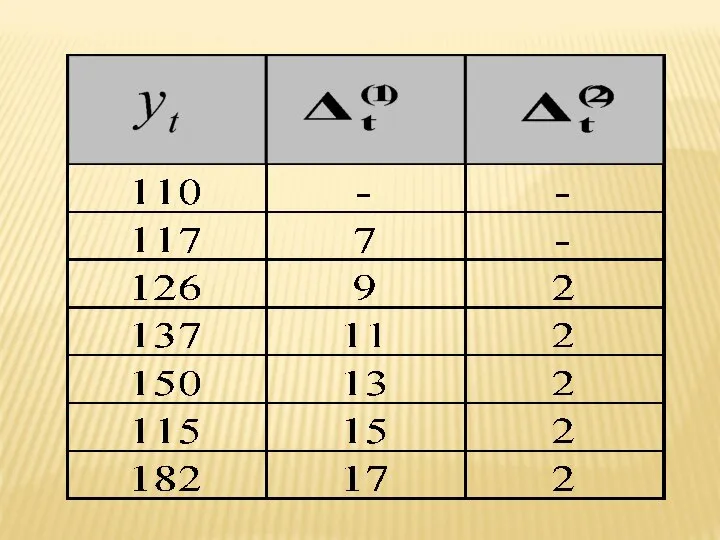
- 91. Выравнивание по параболе второго порядка производится, когда предварительный анализ показывает, что вторые разности примерно равны между
- 93. Для определения параметров применяется метод наименьших квадратов:
- 94. Выравнивание по гиперболе применяется в тех случаях, когда в развитии ряда динамики происходит насыщение
- 96. Для определения параметров используется МНК:
- 97. Выравнивание ряда динамики при помощи показательных функций или экспоненты применяется, когда предварительный анализ показывает: уровень ряда
- 98. Для определения параметров функция приводится предварительно к линейному виду при помощи логарифмирования левой и правой частей
- 100. Скачать презентацию







































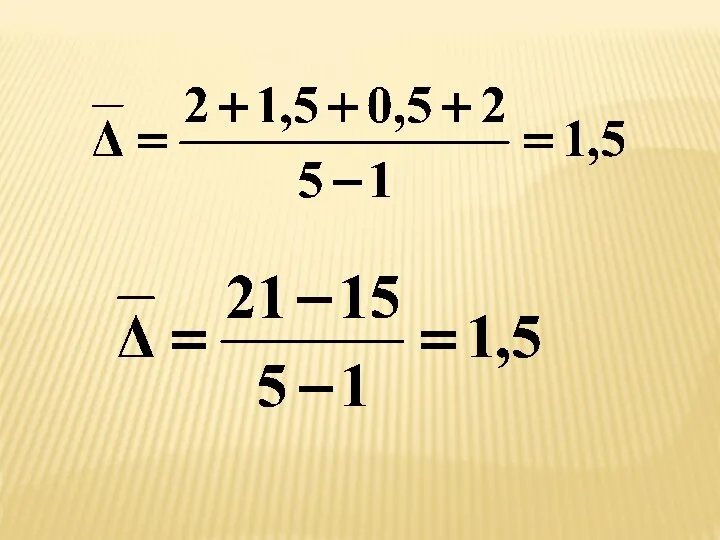



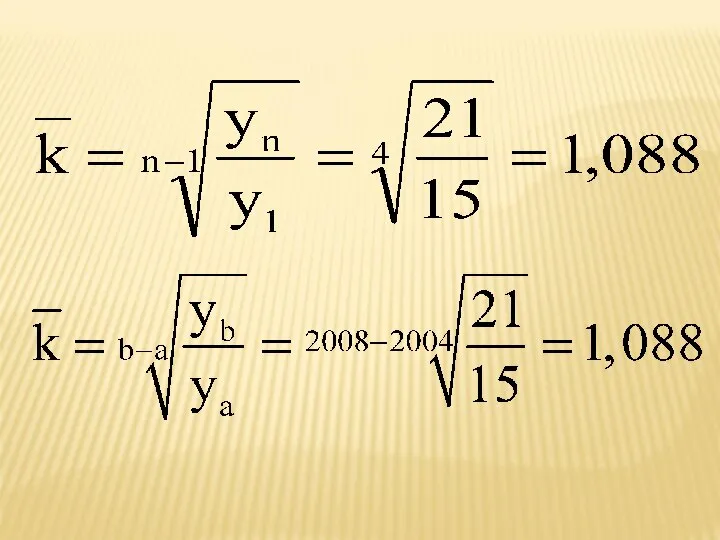



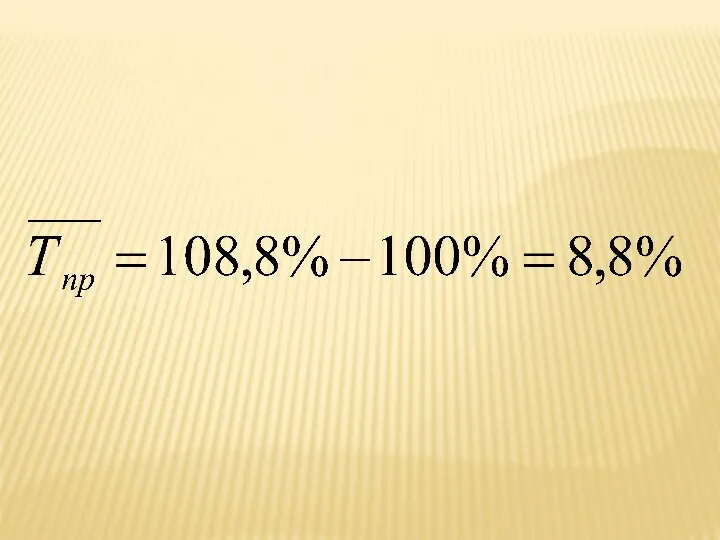



























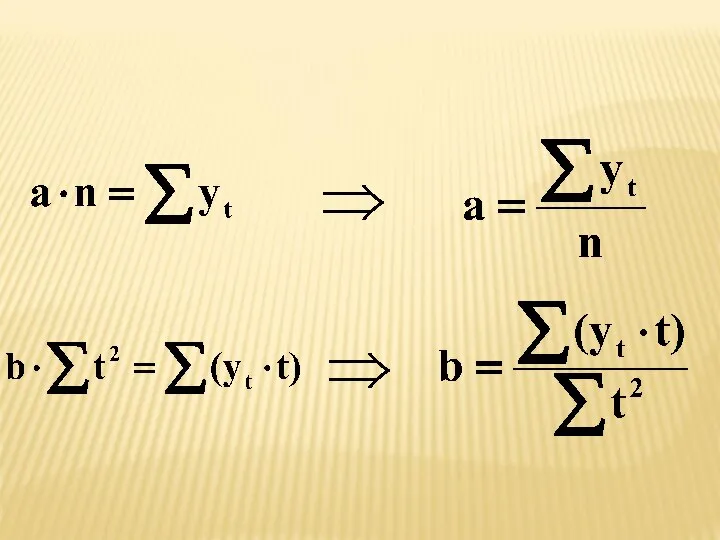
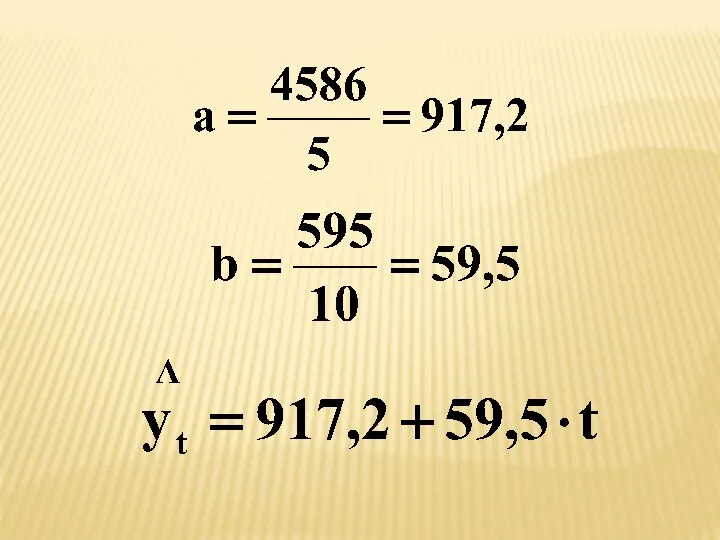








 Вычисление площадей фигур с помощью определенного интеграла
Вычисление площадей фигур с помощью определенного интеграла Подготовка к ЕГЭ 2013 год. В9. Тема: Расстояние в пространстве
Подготовка к ЕГЭ 2013 год. В9. Тема: Расстояние в пространстве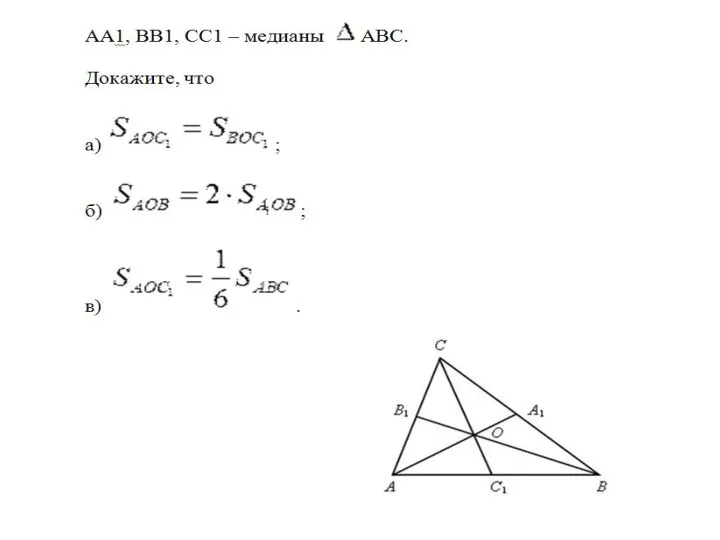 Примеры подобия к доказательству теорем и решению задач. Урок 39
Примеры подобия к доказательству теорем и решению задач. Урок 39 Логические и традиционные головоломки
Логические и традиционные головоломки Презентация на тему Комбинаторика
Презентация на тему Комбинаторика  Поверхностные интегралы первого рода
Поверхностные интегралы первого рода Дифференцирование сложной функции
Дифференцирование сложной функции Понятие о производной функции
Понятие о производной функции Производная функции
Производная функции Урок математики в 4 классе по теме: « Приёмы письменного умножения трёхзначных чисел на однозначные». Урок 5
Урок математики в 4 классе по теме: « Приёмы письменного умножения трёхзначных чисел на однозначные». Урок 5 Плоскости
Плоскости Действия над алгебраическими дробями. 7 класс
Действия над алгебраическими дробями. 7 класс Компланарные вектора
Компланарные вектора Презентация на тему Счёт предметов (1 класс)
Презентация на тему Счёт предметов (1 класс)  Математическая задача
Математическая задача Презентация на тему Зарождение и история геометрии
Презентация на тему Зарождение и история геометрии  Многоугольники в нашей жизни
Многоугольники в нашей жизни Трикутники. Елементи трикутника
Трикутники. Елементи трикутника Фигуры. Геометрия
Фигуры. Геометрия Решение уравнений
Решение уравнений Гипербола
Гипербола Аксиомы
Аксиомы Способы решения уравнений с модулями
Способы решения уравнений с модулями Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе
Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе Эволюционные этапы развития логистики
Эволюционные этапы развития логистики Сравнение десятичных дробей. Работа по учебнику
Сравнение десятичных дробей. Работа по учебнику Тренды графического дизайна
Тренды графического дизайна Умножение и деление десятичных дробей
Умножение и деление десятичных дробей