Слайд 2Аксиомы планиметрии
1. принадлежности(2)
2. порядка(3)
3. измерения отрезков(2)
измерения углов(2)
4. Отложения углов(2)
5. параллельности(1)

Слайд 3Какова бы не была прямая, есть точки, принадлежащие и не принадлежащие ей.
Через

любые две точки можно провести прямую, причём только одну.
Слайд 4Из трёх точек на прямой одна и только одна лежит между двумя

другими.
Точка, лежащая на прямой, делит эту прямую на две полупрямые.
Прямая разбивает плоскость на две полуплоскости.
Слайд 5Каждый отрезок имеет определённую длину, большую нуля.
Если точка, принадлежащая отрезку, лежит между

его концами, то длина данного отрезка равна сумме длин образовавшихся отрезков.
Слайд 63. Каждый угол имеет определённую градусную меру, большую нуля.
4. Если луч исходит

из вершины угла и проходит между его сторонами, тогда данный угол равен сумме образовавшихся углов.
Слайд 7Каков бы ни был луч, начиная от его начальной точки, на нём

можно отложить отрезок данной длины,
и только одним способом.
От любого луча в заданную полуплоскость можно отложить угол заданной величины, меньшей 1800,
и только один.
Слайд 8Через точку, лежащую вне данной прямой на плоскости, можно провести одну и

только одну прямую, параллельную данной прямой.







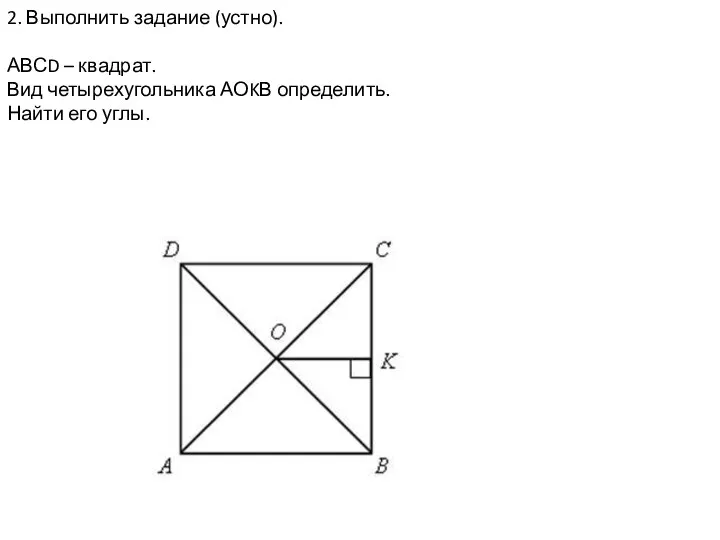 Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 ВПР вариант 16 № 11. Решение трудной задачи
ВПР вариант 16 № 11. Решение трудной задачи Математический язык
Математический язык Презентация на тему НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ
Презентация на тему НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ  Четные и нечетные числа
Четные и нечетные числа 1_urok_algebry_v_8_klasse
1_urok_algebry_v_8_klasse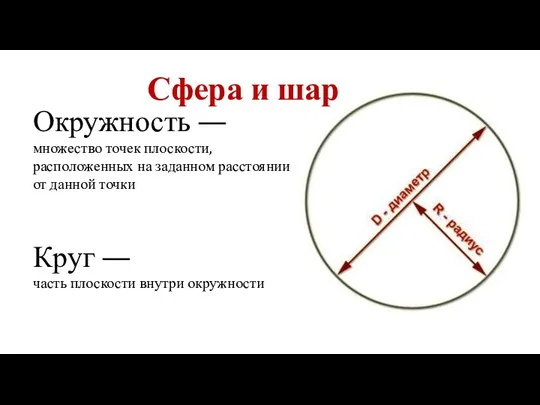 Сфера и шар
Сфера и шар Учимся складывать столбиком
Учимся складывать столбиком Работа переменной силы
Работа переменной силы Математическая логика и теория алгоритмов. Алгебра логики. Часть 2
Математическая логика и теория алгоритмов. Алгебра логики. Часть 2 Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис
Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис Задачи по геометрии 11 класс
Задачи по геометрии 11 класс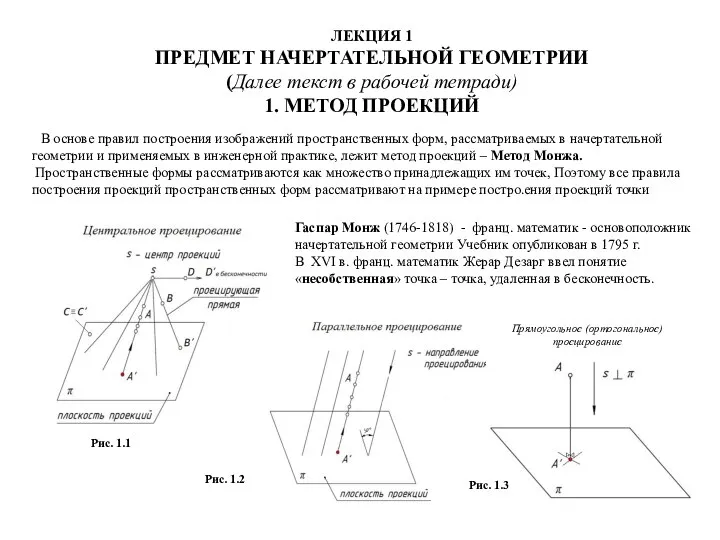 Предмет начертательной геометрии. Метод проекций. (Лекция 1)
Предмет начертательной геометрии. Метод проекций. (Лекция 1) Показательные неравенства
Показательные неравенства Интервальное оценивание
Интервальное оценивание Весёлый счёт
Весёлый счёт Функция нескольких действительных переменных. Условный экстремум
Функция нескольких действительных переменных. Условный экстремум Основы алгебры логики
Основы алгебры логики Человек трудолюбивый – самый счастливый– самый
Человек трудолюбивый – самый счастливый– самый Правила деления. (6 класс)
Правила деления. (6 класс) Преобразование графиков функций
Преобразование графиков функций Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства Математический калейдоскоп. Мероприятие для учащихся 5 классов
Математический калейдоскоп. Мероприятие для учащихся 5 классов Критерий углового преобразования Фишера
Критерий углового преобразования Фишера Могла ли математика спасти Пахома, или Площадь
Могла ли математика спасти Пахома, или Площадь Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Построение фронтальной диметрической и изометрической проекций
Построение фронтальной диметрической и изометрической проекций B1. Практический расчет, оценка и прикидка
B1. Практический расчет, оценка и прикидка