Содержание
- 2. План лекции 1. Абсолютные показатели вариации 2. Относительные показатели вариации 3.Меры вариации для сгруппированных данных 4.Правило
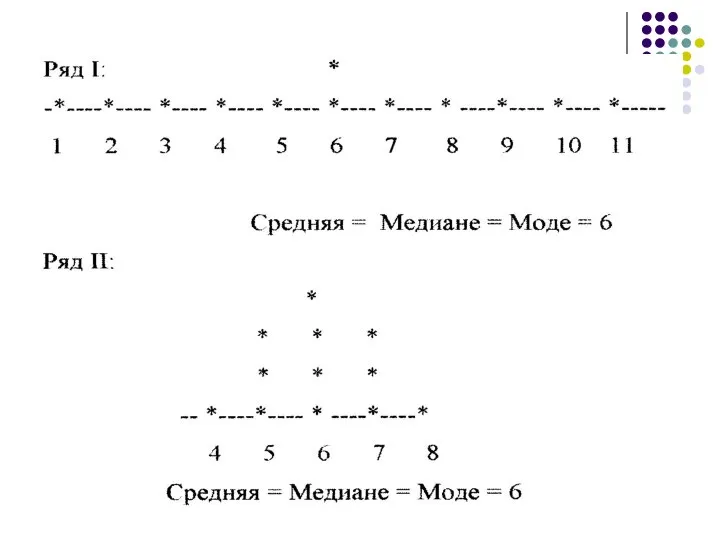
- 3. Ряд I: 1, 2, 3, 4, 5, 6, 6, 7, 8, 9, 10, 11 Ряд II:
- 5. Интерквартильный размах – разница между первым и третьим квартилями. Чем больше величина интерквартильного размаха, тем больше
- 6. Размах вариации - разность между наибольшим и наименьшим значениями признака
- 7. Сумма отклонений всех вариантов от их средней арифметической, согласно свойству средней арифметической, всегда равна нулю.
- 10. Дисперсия вариационного ряда есть средняя арифметическая квадрата отклонения (средний квадрат отклонения) значений признаков ряда от их
- 11. Среднее квадратическое (стандартное) отклонение вариационного ряда есть арифметическое значение корня квадратного из дисперсии.
- 12. Среднее квадратическое (стандартное) отклонение вариационного ряда есть арифметическое значение корня квадратного из дисперсии.
- 13. Показатели относительного рассеяния Расчет показателей меры относительного рассеяния осуществляют как отношение абсолютного показателя вариации признака к
- 14. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней:
- 15. Относительное линейное отклонение характеризует долю усредненного значения признака абсолютных отклонений от средней величины:
- 16. Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин:
- 17. Предположим, что стандартное отклонение в выборке валютных счетов в банке «А» и банке «В» равно $20.
- 18. Сравнивая эти два случая, можно сказать, что такая абсолютная мера рассеяния как стандартное отклонение не передает
- 19. Однако у такого способа оценки вариации есть и существенный недостаток. Например, исходная совокупность рабочих, имеющих средний
- 20. Меры вариации для сгруппированных данных. Правило сложения дисперсий Вариация признаков, как правило, обусловлена влиянием различных факторов.
- 21. Для этих целей используются показатели вариации для сгруппированных данных. В этом случае выделяют три вида дисперсий:
- 23. Вычислим m частных средних
- 24. …
- 25. На основе частных средних определяем общую среднюю , где
- 26. Общая дисперсия отражает вариацию признака за счет всех условий, действующих в совокупности
- 27. Межгрупповая дисперсия отражает вариацию между группами за счет фактора, положенного в основу группировки
- 28. Частная групповая дисперсия отражает вариацию внутри каждой группы
- 29. …….
- 30. В общем виде частная дисперсия: где Nij- частоты для значений xi, в каждой j-группе, j=1,…,m.
- 31. Внутригрупповая дисперсия - средняя арифметическая из групповых дисперсий
- 32. Общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий Суть правила: общая дисперсия, возникающая
- 33. С помощью правила сложения дисперсий оценивается удельный вес факторов, лежащих в основе группировки, во всей совокупности
- 34. Эмпирическое корреляционное отношение
- 35. Показатель принимает значения в интервале [0, 1] и и характеризует взаимосвязь между изучаемым признаком и признаком,
- 36. Промежуточные значения η оцениваются по степени их близости к граничным
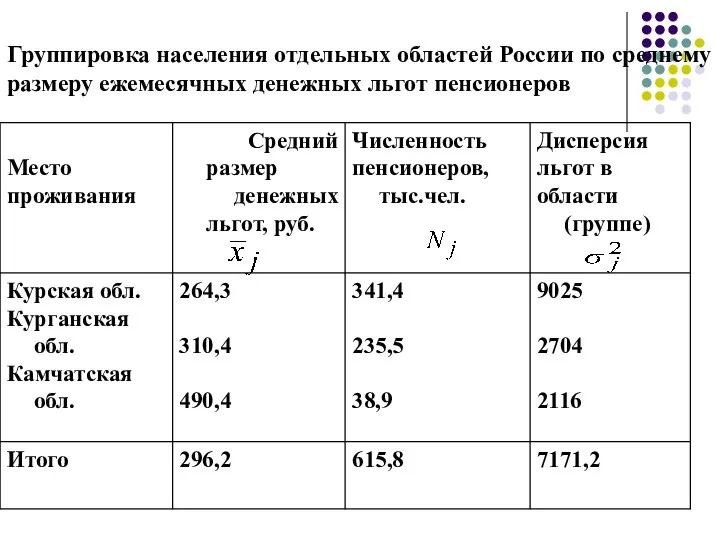
- 37. Группировка населения отдельных областей России по среднему размеру ежемесячных денежных льгот пенсионеров
- 38. Найдем средний размер льгот (руб.) по трем областям в целом:
- 39. Вариация льгот по отдельным областям, обусловленная различием в месте проживания пенсионеров, характеризуется межгрупповой дисперсией:
- 40. Средняя из групповых дисперсий дает обобщающую характеристику случайной вариации, обусловленную отдельными факторами, кроме места проживания пенсионеров
- 41. Вариация льгот в изучаемых областях России, обусловленная влиянием всех факторов, вместе взятых, определяется общей дисперсией:
- 43. Полученный коэффициент детерминации показывает, что дисперсия льгот зависит от места проживания пенсионеров на 32,5 %. Остальные
- 44. Вариация альтернативного признака При статистическом выражении колеблемости альтернативных признаков наличие изучаемого признака обозначается 1, а его
- 48. Если значения 1 и 0 встречаются одинаково часто, то дисперсия достигает своего максимума Пример. На 10000
- 49. Внутригрупповая дисперсия доли Средняя из внутригрупповых дисперсий
- 50. межгрупповая дисперсия
- 51. где ni – численность единиц в отдельных группах; – доля изучаемого признака во всей совокупности, которая
- 52. Общая дисперсия Правило сложения дисперсии доли признака
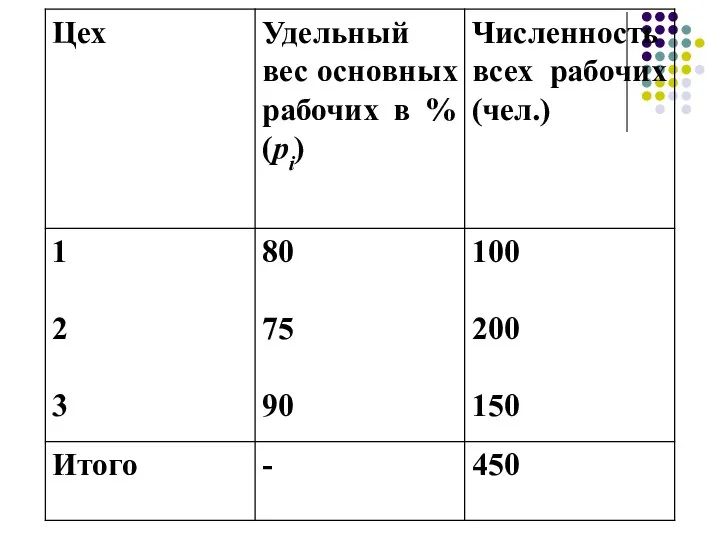
- 54. Определим долю рабочих в целом по фирме:
- 55. Общая дисперсия доли основных рабочих по всей фирме в целом будет равна:
- 56. Внутрицеховые дисперсии:
- 57. Средняя из внутрицеховых дисперсий: Межгрупповая дисперсия:
- 59. Скачать презентацию





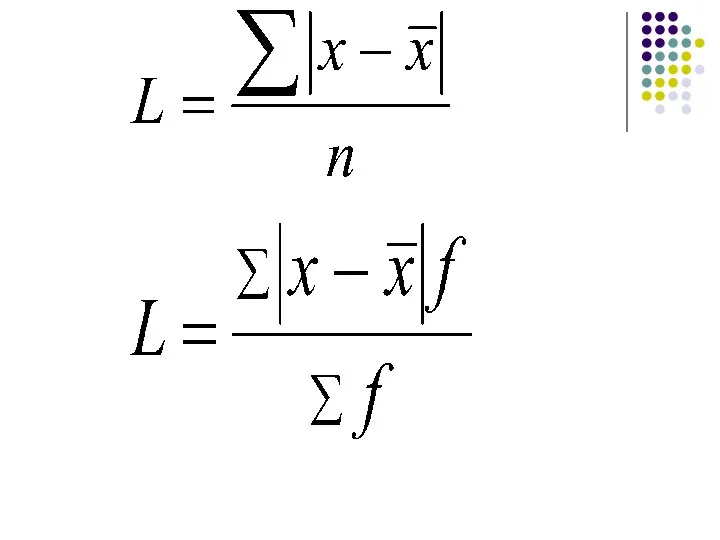
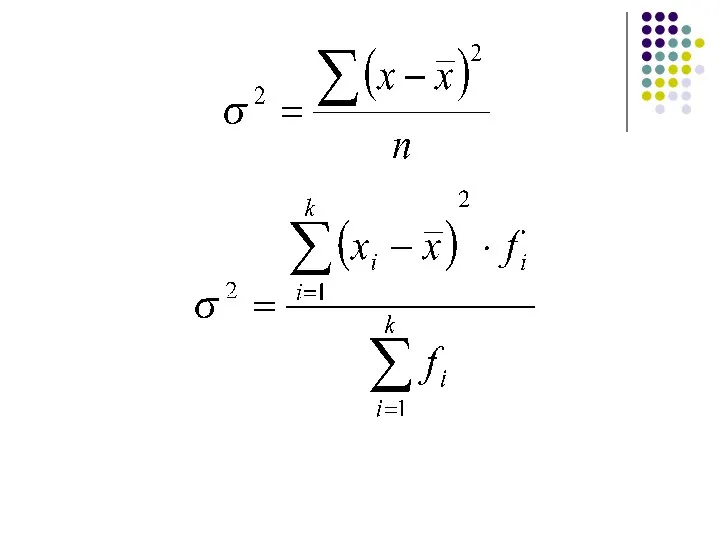














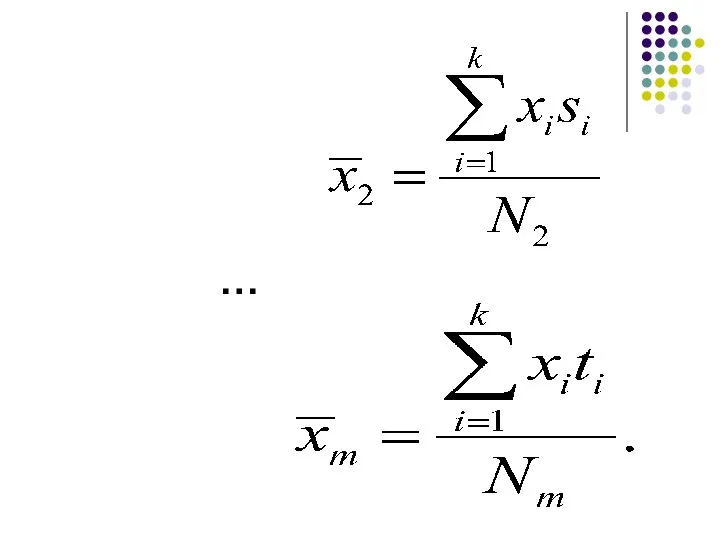
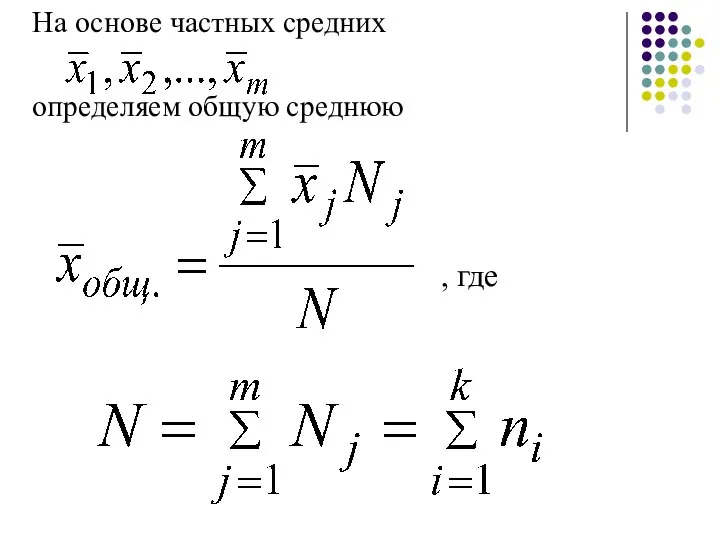



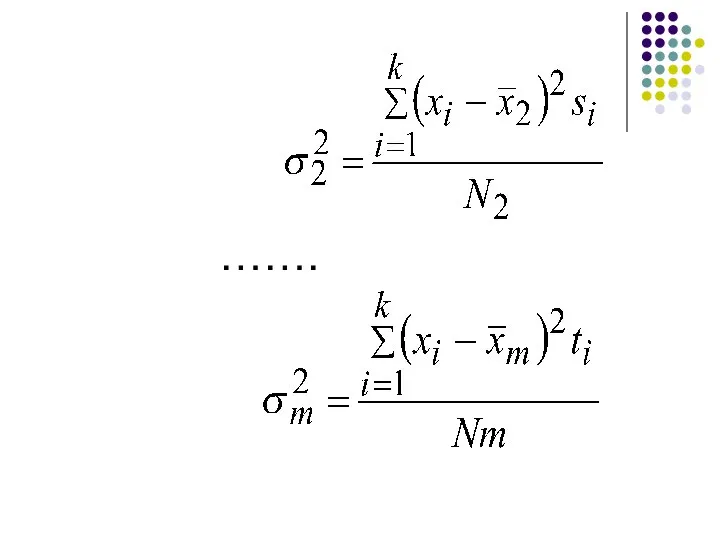





![Показатель принимает значения в интервале [0, 1] и и характеризует взаимосвязь между](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1174279/slide-34.jpg)





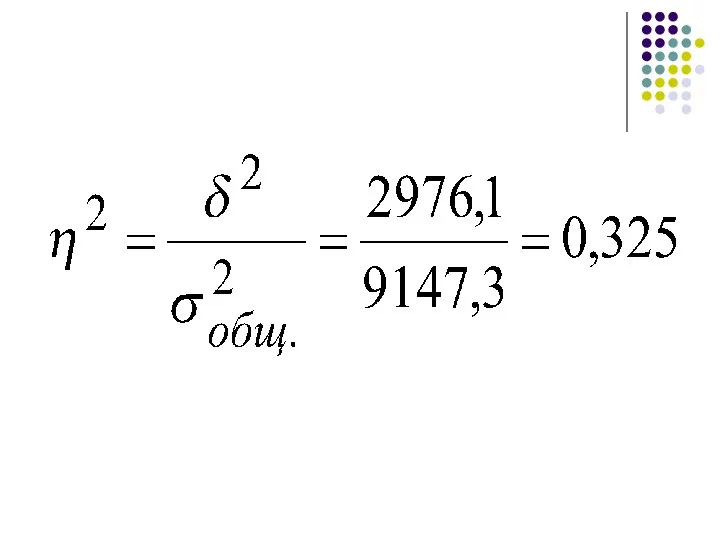


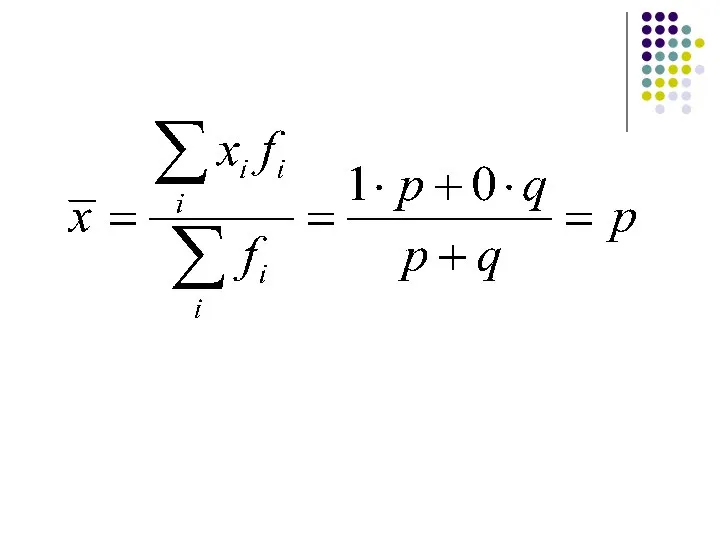
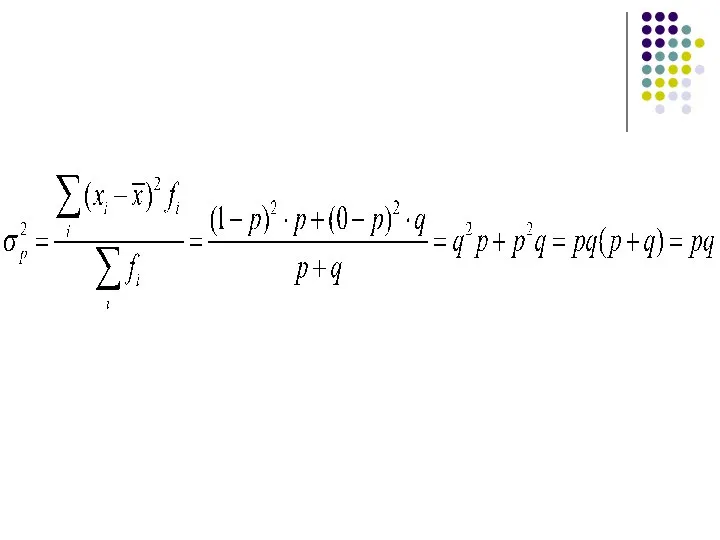

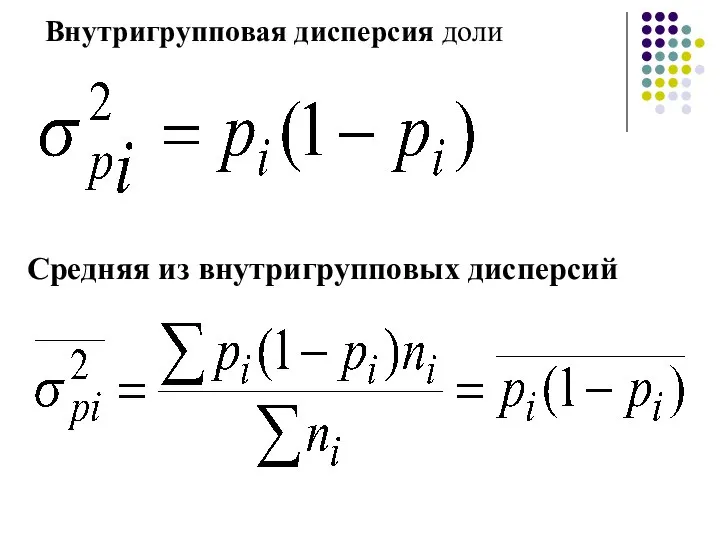







 Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Решение задач с помощью составления систем уравнений. 9 класс
Решение задач с помощью составления систем уравнений. 9 класс Арифметический диктант
Арифметический диктант Занимательный устный счет
Занимательный устный счет Письменное вычитание с переходом через десяток в случаях: 50 - 24
Письменное вычитание с переходом через десяток в случаях: 50 - 24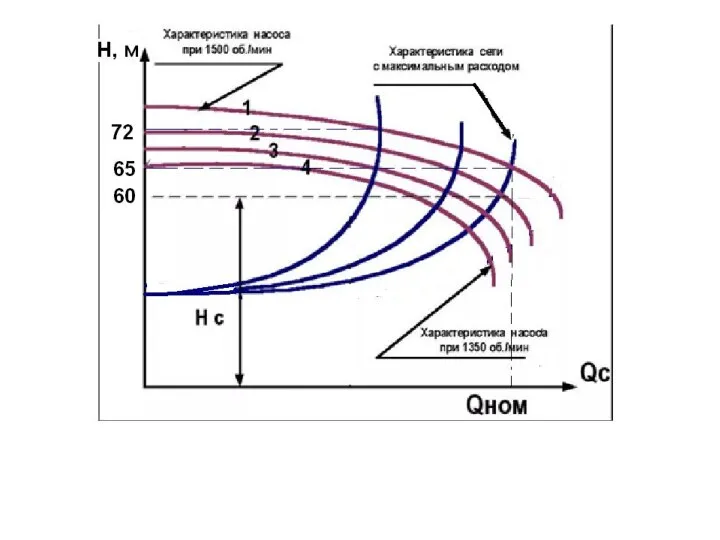 Модель частотно-регулируемого привода. (Тема 8)
Модель частотно-регулируемого привода. (Тема 8) Усеченный цилиндр
Усеченный цилиндр Свойство противоположных сторон прямоугольника
Свойство противоположных сторон прямоугольника Решение задач
Решение задач جمع%20و%20تفریق%20اعداد%20مرکب%20و%20الگوها
جمع%20و%20تفریق%20اعداد%20مرکب%20و%20الگوها Применение метода интервалов для решения неравенств. 8 класс
Применение метода интервалов для решения неравенств. 8 класс Решение планиметрических задач
Решение планиметрических задач Объединение множеств
Объединение множеств Ряды. Лекция
Ряды. Лекция Полином Жегалкина
Полином Жегалкина Космическая игра. Таблица умножения
Космическая игра. Таблица умножения Равнобедренный треугольник
Равнобедренный треугольник Математика вокруг нас
Математика вокруг нас Две задачи на дроби
Две задачи на дроби Руководитель кружка по математике для 7 класса
Руководитель кружка по математике для 7 класса Матрицы и действия над ними
Матрицы и действия над ними Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов
Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов Дистанционный конкурс Царство ребусов
Дистанционный конкурс Царство ребусов Непрерывно-стохастические модели
Непрерывно-стохастические модели Преобразования графиков
Преобразования графиков Отношение чисел
Отношение чисел Площадь треугольника и биссектриса
Площадь треугольника и биссектриса Советы и хитрости для решения задач на ОГЭ по математике
Советы и хитрости для решения задач на ОГЭ по математике