Содержание
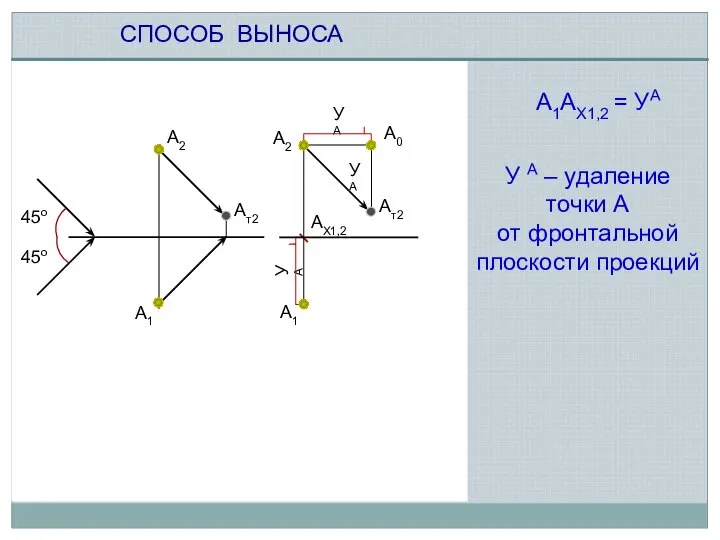
- 2. СПОСОБ ВЫНОСА 45о 45о Ат2 А2 Ат2 А2 А1 А1АХ1,2 = УА УА УА А0 УА
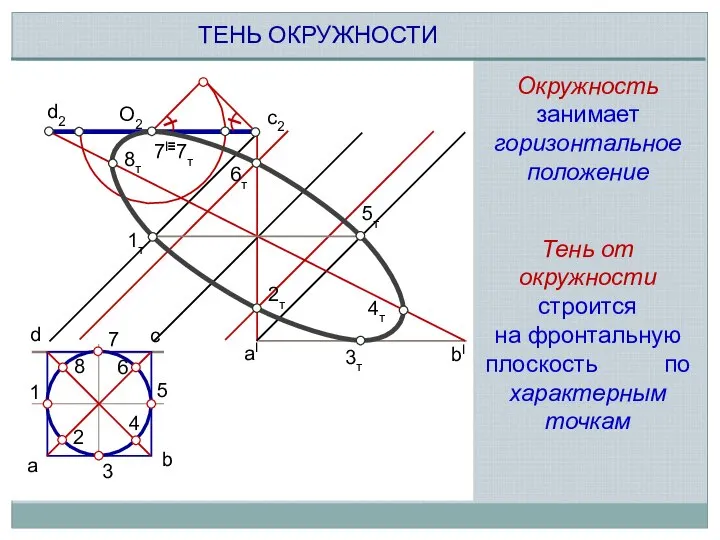
- 3. 1 2 3 4 5 6 7 8 8т 3т a d c b aI bI
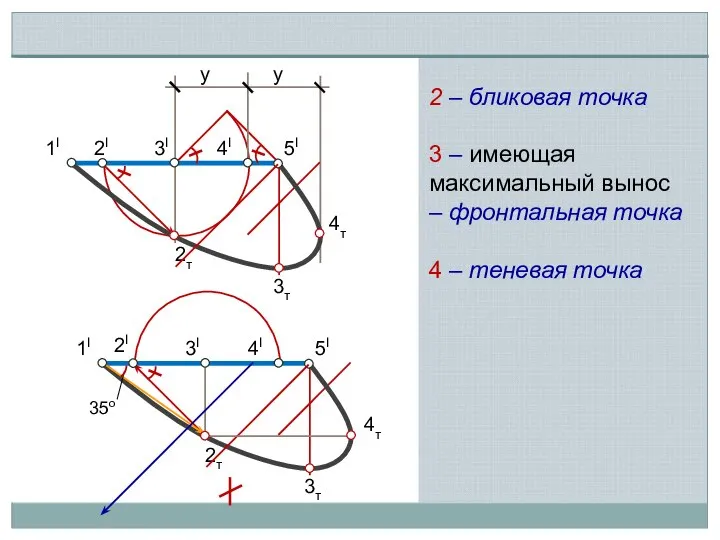
- 4. 3I 1I 2I 4I 5I у у 2т 3т 4т 3I 1I 2I 4I 5I 2т
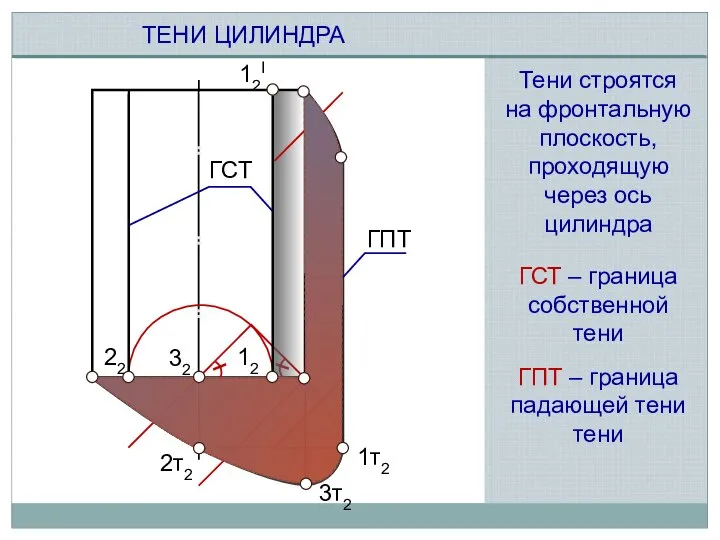
- 5. 12 22 12I 32 2т2 3т2 1т2 ТЕНИ ЦИЛИНДРА ГСТ ГСТ – граница собственной тени ГПТ
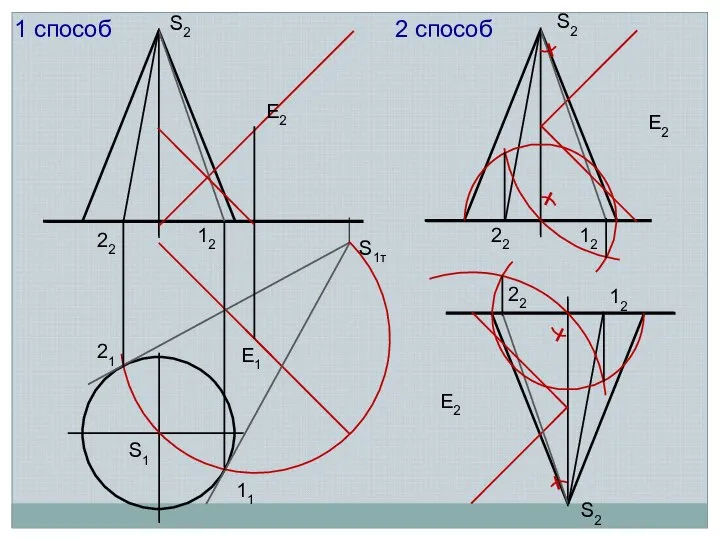
- 6. ТЕНИ КОНУСА
- 7. 21 S1 11 S1т S2 Е1 S2 S2 22 12 12 12 22 22 Е2 Е2
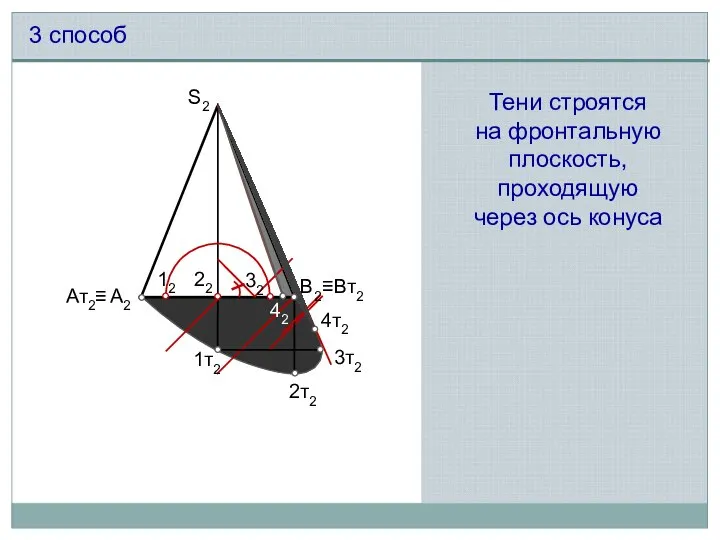
- 8. S2 42 12 22 32 1т2 2т2 3т2 4т2 А2 В2 Ат2≡ ≡Вт2 3 способ Тени
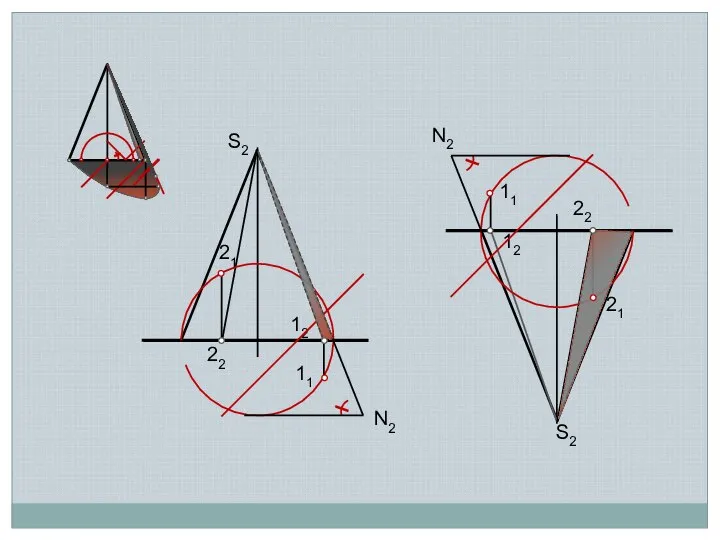
- 9. S2 12 22 N2 21 11 11 S2 12 22 N2 21
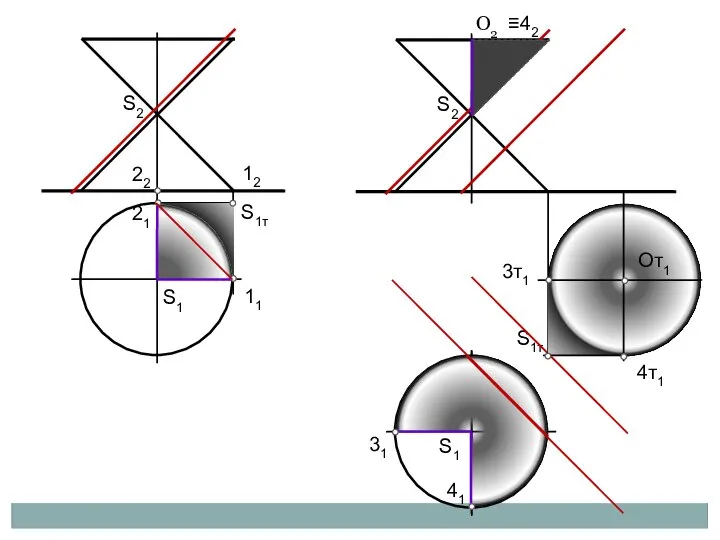
- 10. ТЕНЬ КОНУСА с углом наклона образующей к основанию равным 45О
- 11. 21 S1 11 S1т S2 22 12 S1т S2 S1 31 41 О2 От1 3т1 4т1
- 12. Касательным конусом с образующей под 45о будут определяться точки границы собственной тени на фронтальном и профильном
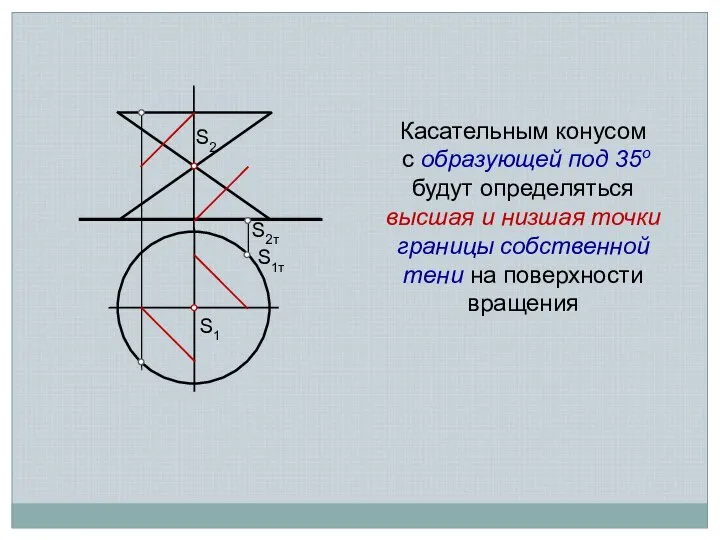
- 13. S1 S1т S2 S2т Касательным конусом с образующей под 35о будут определяться высшая и низшая точки
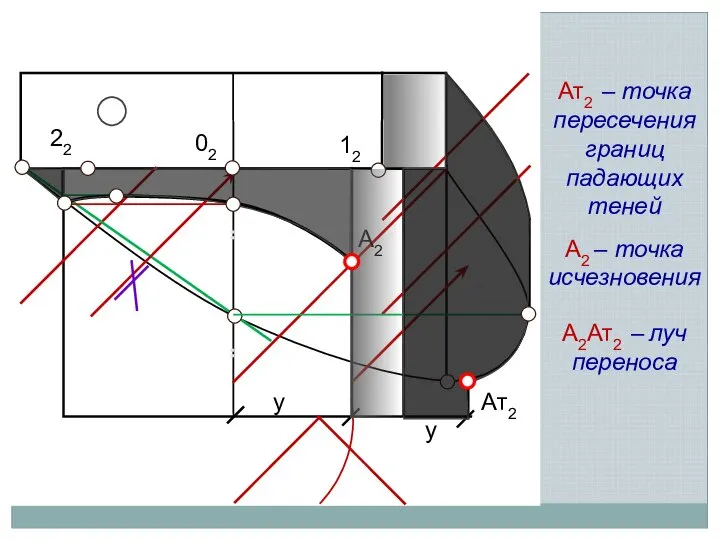
- 14. 12 22 02 Ат2 А2 – точка исчезновения А2 Ат2 – точка пересечения границ падающих теней
- 15. Точка исчезновения находится на пересечении границ падающей и собственной тени поверхности В точке пересечения граница падающей
- 16. ТЕНИ КОМБИНИРОВАННЫХ ПОВЕРХНОСТЕЙ
- 17. 12 22 02 Ат2 А2 Когда две поверхности имеют общую линию пересечения, то границы собственных теней
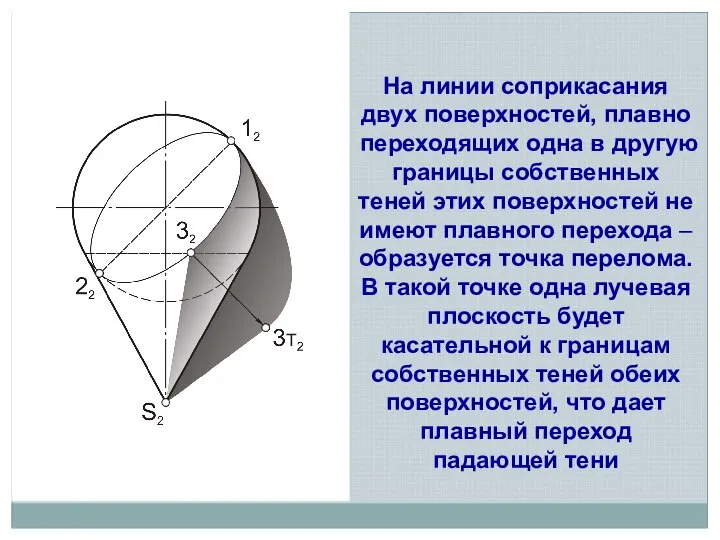
- 18. На линии соприкасания двух поверхностей, плавно переходящих одна в другую границы собственных теней этих поверхностей не
- 19. СПОСОБ КОНУСОВ И ЦИЛИНДРОВ
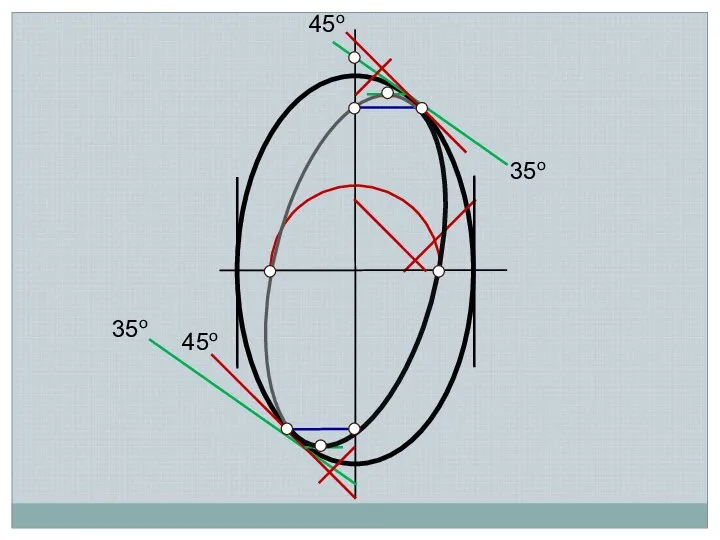
- 21. 35о 45о 35о 45о
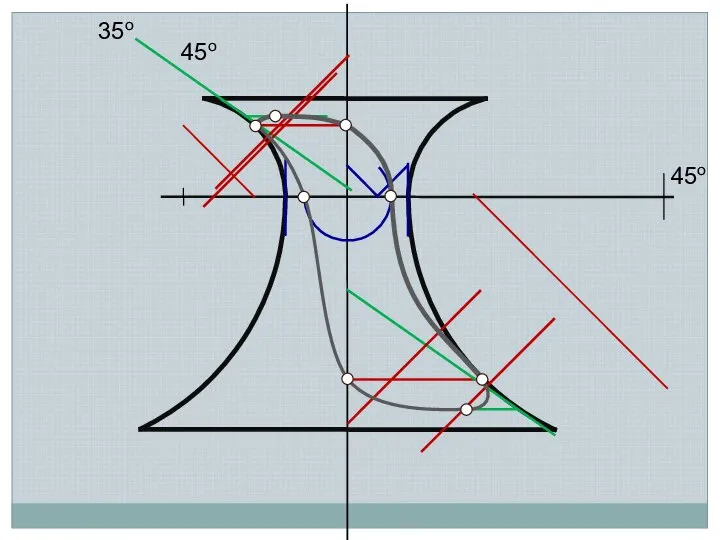
- 22. 35о 45о 45о
- 23. СПОСОБ ЦИЛИНДРИЧЕСКИХ ЭКРАНОВ
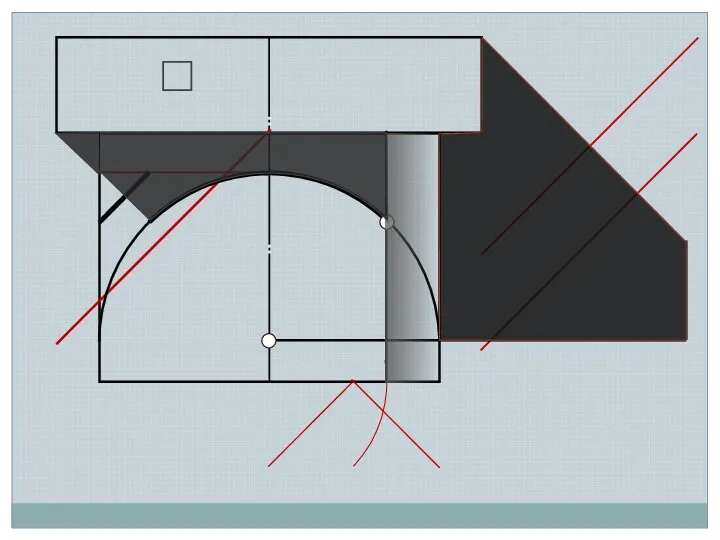
- 25. Падающую тень от квадратной плиты на поверхность вращения удобно строить, используя «цилиндрические экраны» Тень от квадратной
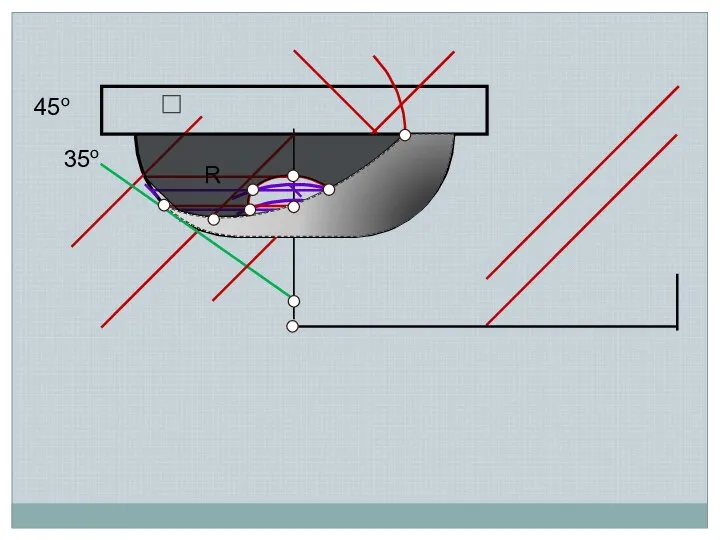
- 26. R 35о 45о
- 28. Скачать презентацию










 Дискретные случайные величины
Дискретные случайные величины Решение тригонометрического уравнения
Решение тригонометрического уравнения Внеклассное мероприятие. Путешествие в мир многогранников
Внеклассное мероприятие. Путешествие в мир многогранников Задачи на расстояние
Задачи на расстояние Параллельность_прямых_в_пространстве_2019
Параллельность_прямых_в_пространстве_2019 Дроби. 5 класс
Дроби. 5 класс Производная частного двух функций
Производная частного двух функций Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Измерение параллеппипеда
Измерение параллеппипеда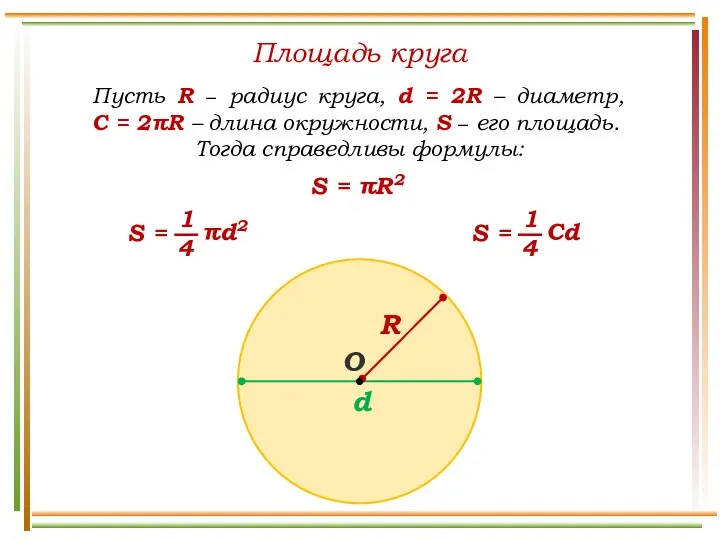 Площадь круга
Площадь круга Презентация на тему Повторение математики 5 класс
Презентация на тему Повторение математики 5 класс  Презентация на тему Решение уравнений, содержащих несколько знаков модуля
Презентация на тему Решение уравнений, содержащих несколько знаков модуля  Квадратные неравенства
Квадратные неравенства Решение интеграла
Решение интеграла Предел функции в точке
Предел функции в точке Построение треугольника
Построение треугольника Распределенные системы. Математическое представление распределенной системы
Распределенные системы. Математическое представление распределенной системы Логарифмы вокруг нас
Логарифмы вокруг нас Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Правильные многоугольники в природе. Геометрия пчелиных сот
Правильные многоугольники в природе. Геометрия пчелиных сот Повторение 1 класс
Повторение 1 класс Задачи математической статистики
Задачи математической статистики Это страшное слово: Параметр
Это страшное слово: Параметр Линии второго порядка
Линии второго порядка Methodical Problems of Comparative Studies
Methodical Problems of Comparative Studies Финансовая грамотность
Финансовая грамотность Решение задач с помощью составления систем уравнений. 9 класс
Решение задач с помощью составления систем уравнений. 9 класс Правильные многоугольники
Правильные многоугольники