Треугольник. Геометрия (7 класс)

Цель :
Повторить понятия:
треугольника,
углов треугольника,
остроугольного треугольника,
тупоугольного треугольника,
прямоугольного треугольника,
равнобедренного треугольника,
равностороннего треугольника,
равных треугольников.

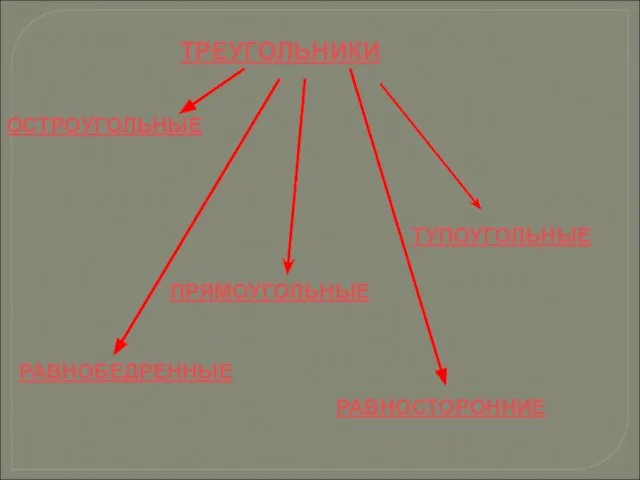
ТРЕУГОЛЬНИКИ
ОСТРОУГОЛЬНЫЕ
ПРЯМОУГОЛЬНЫЕ
ТУПОУГОЛЬНЫЕ
РАВНОБЕДРЕННЫЕ
РАВНОСТОРОННИЕ

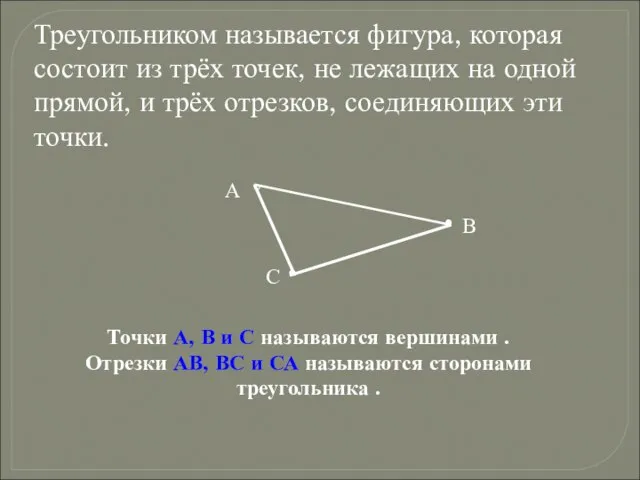
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки.
В
А
С
Точки А, В и С называются вершинами .
Отрезки АВ, ВС и СА называются сторонами
треугольника .

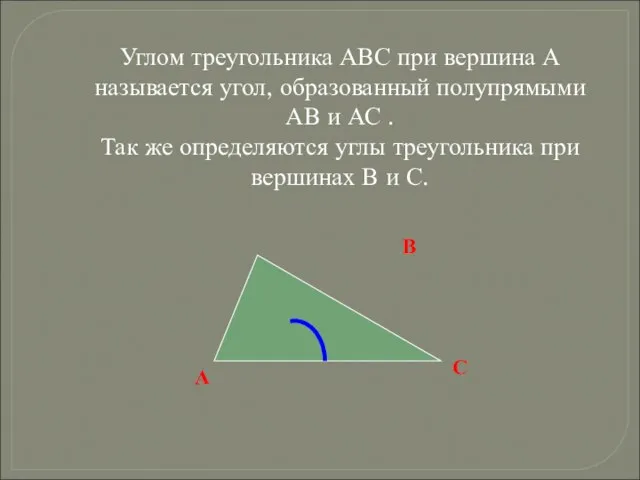
Углом треугольника АВС при вершина А называется угол, образованный полупрямыми АВ и АС .
Так же определяются углы треугольника при вершинах В и С.
А
В
С

Треугольник называется остроугольным, если у него все углы острые
В
С
А

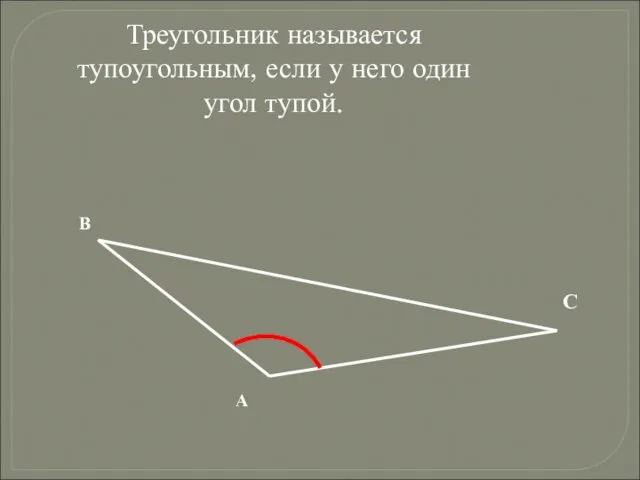
Треугольник называется тупоугольным, если у него один угол тупой.
А
В
С

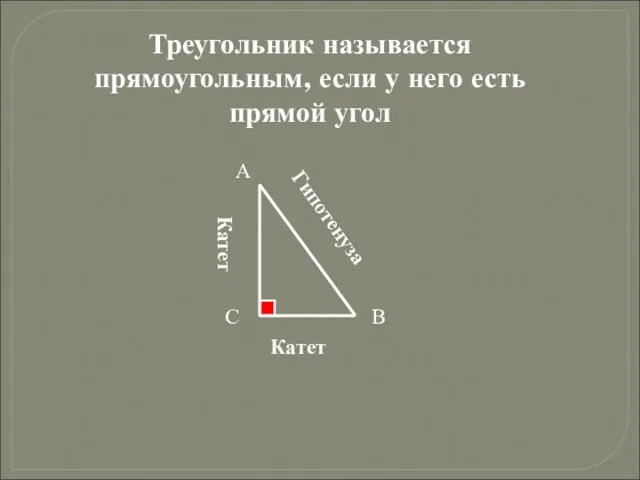
Треугольник называется прямоугольным, если у него есть прямой угол
А
В
С
Гипотенуза
Катет
Катет

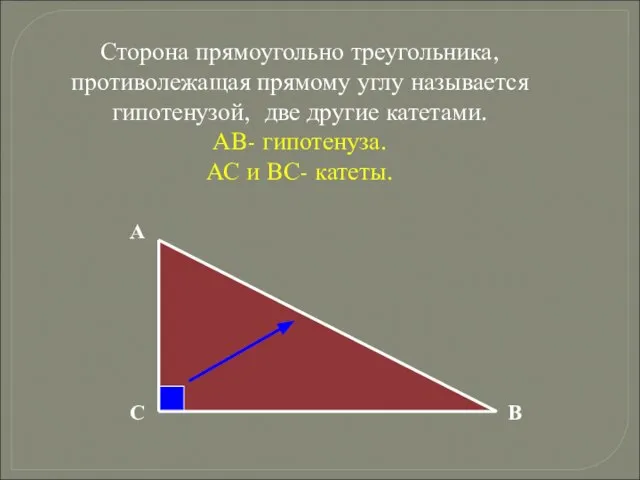
Сторона прямоугольно треугольника, противолежащая прямому углу называется гипотенузой, две другие катетами.
АВ- гипотенуза.
АС и ВС- катеты.
А
В
С

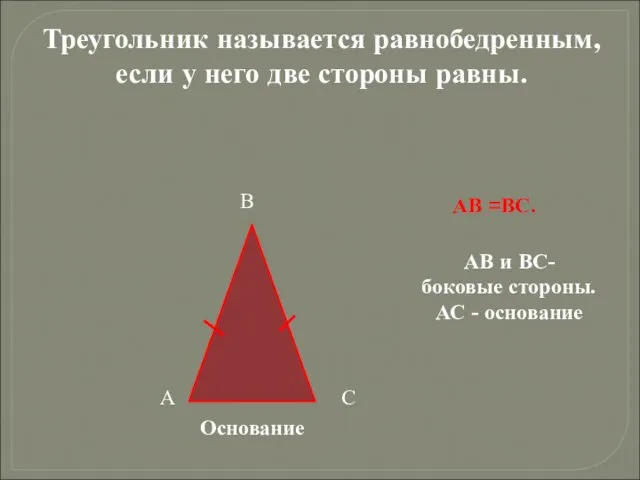
Треугольник называется равнобедренным,
если у него две стороны равны.
А
В
С
Основание
АВ =ВС.
АВ и ВС-
боковые стороны.
АС - основание

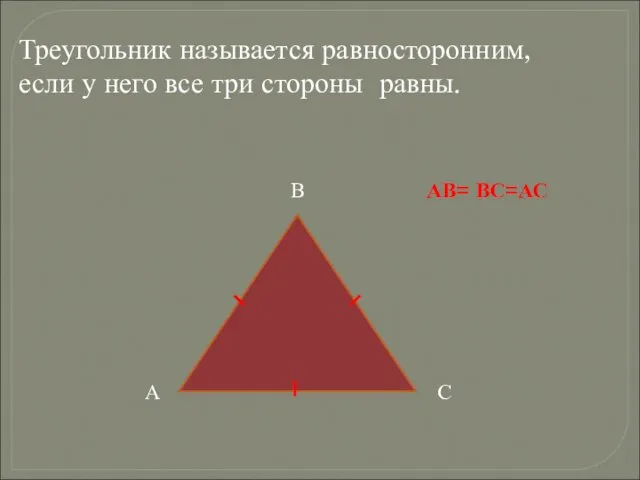
Треугольник называется равносторонним,
если у него все три стороны равны.
АВ= ВС=АС
А
В
С

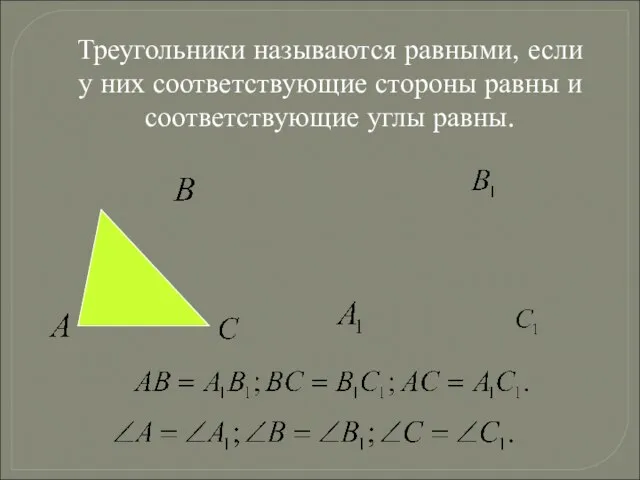
Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны.

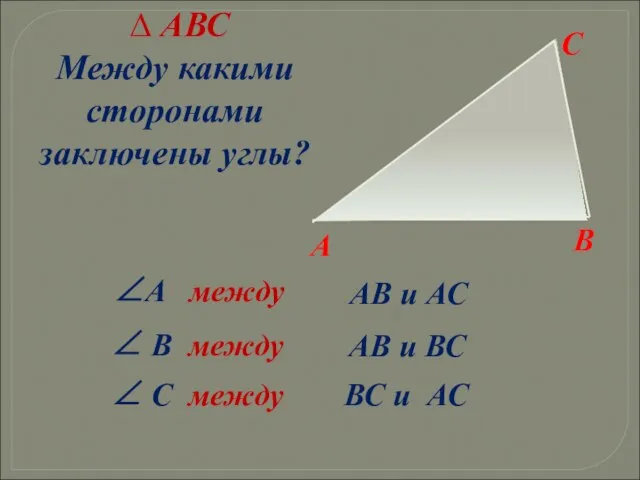
∠ В между
∆ АВС
Между какими сторонами заключены углы?
АВ и ВС
∠ С между
∠A между
АВ и АС
ВС и АС

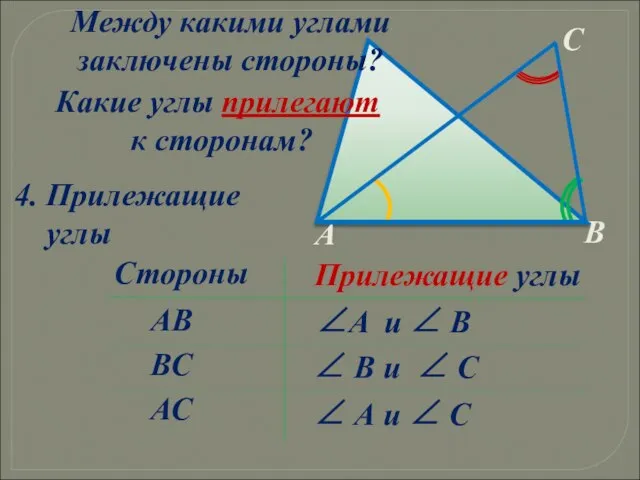
∠ В и ∠ С
Между какими углами заключены стороны?
ВС
∠ А и ∠ С
∠A и ∠ В
АВ
АС
Стороны
Прилежащие углы
Какие углы прилегают
к сторонам?
4. Прилежащие
углы

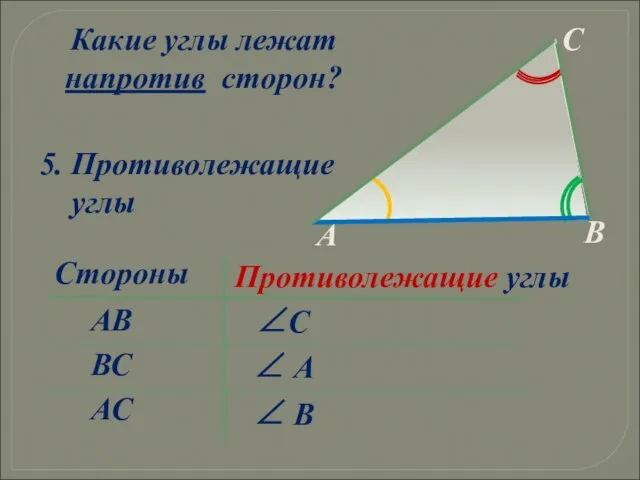
∠ А
ВС
∠ В
∠С
АВ
АС
Стороны
Противолежащие углы
Какие углы лежат напротив сторон?
5. Противолежащие
углы

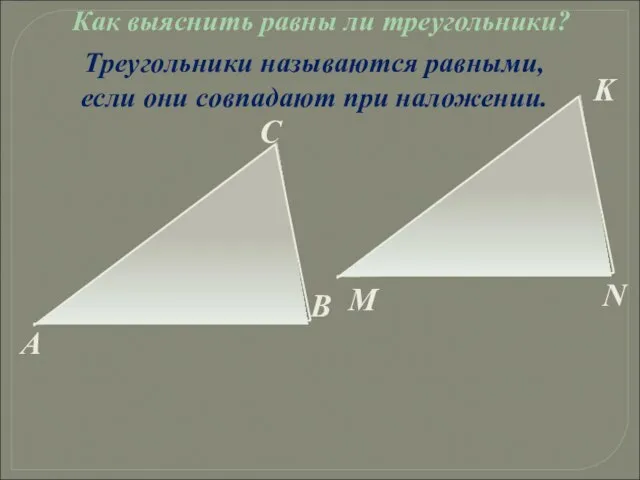
Треугольники называются равными,
если они совпадают при наложении.
Как выяснить равны ли треугольники?

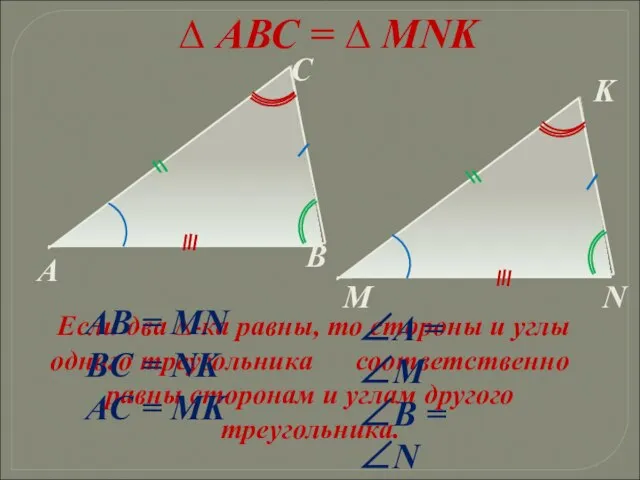
∆ АВС = ∆ MNK
Если два ∆-ка равны, то стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника.
АВ = MN
BС = NK
AC = MK
∠A = ∠M
∠B = ∠N
∠C = ∠K

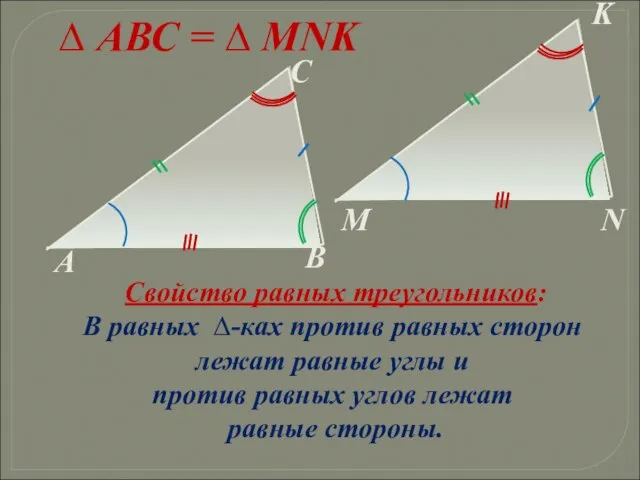
∆ АВС = ∆ MNK
Свойство равных треугольников:
В равных ∆-ках против равных сторон
лежат равные углы и
против равных углов лежат
равные стороны.