Углы, образованные хордами, секущими, касательными. Свойство отрезков хорд и касательных

Углы, образованные хордами, секущими, касательными.

Свойство 1. Угол между секущей и касательной, проходящими через одну точку вне окружности, равен полуразности дуг, заключённых внутри угла и ограниченных точками пересечения и точкой касания
Свойство 2. Угол между двумя касательными, проходящими через одну точку вне окружности, равен полуразности дуг, заключённых внутри угла и ограниченных точками касания.

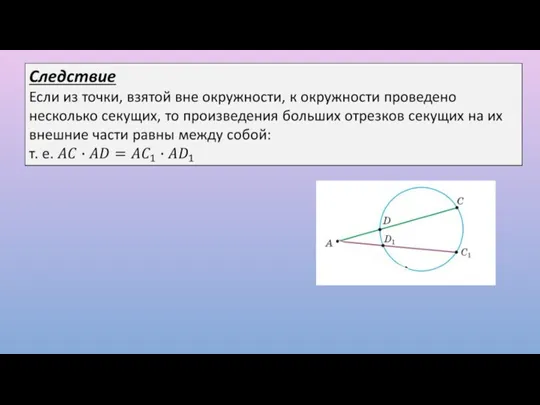
Свойство пересекающихся
хорд
Произведения отрезков пересекающихся хорд равны между собой.

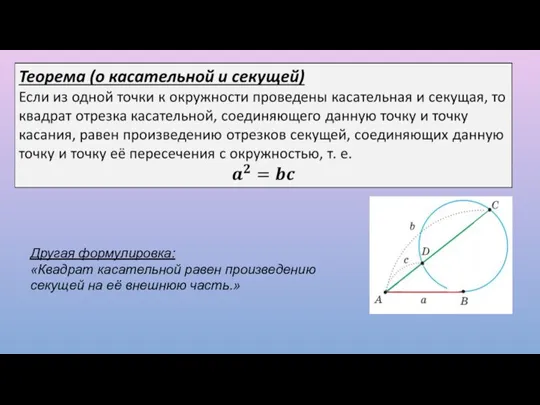
Свойство отрезков хорд и касательных

Другая формулировка:
«Квадрат касательной равен произведению секущей на её внешнюю часть.»

Задача 9.Хорды AB и CD окружности пересекаются в точке F, которая является серединой хорды AB. Вычислите длину хорды AB, если СD=25 см и CF = 9 см и AF=FB

Задача 10.Радиус круга равен 7,5 см. Точка P лежит внутри круга на расстоянии 6,5 см от его центра O. Через точку P проведена хорда AB, длина которой равна 9 см. Вычислите длины отрезков, на которые точка P делит хорду AB.

Задача 11. Из точки A к окружности проведены касательная AB и секущая AC, при этом отрезок AC пересекается с окружностью в точке D. При этом секущая оказалась в 3 раза больше касательной. Найдите длину секущей, если AD=2 см.

Задача 12. Хорды AB и CD окружности пересекаются в точке O. Вычислите длины отрезков DO и OC, если AO=4 см, BO=6 см, а длина отрезка DO на 5 см больше длины отрезка CO.

Задача 13. Диаметр AB и хорда CD окружности перпендикулярны и пересекаются в точке O. Вычислите радиус окружности, если AO=2 см, а длина хорды CD на 2 см меньше диаметра окружности.

Ответ: 1,5 см; 2 см.
Задача 14. В треугольнике ABC AB=2 см, BC=4 см, CA=3 см. Окружность, проходящая через вершины B и C, пересекает прямую AC в точке K, лежащей на луче CA, а прямую AB – в точке T. Известно, что AK=1 см. Вычислите длины отрезков AT и KT.