Содержание
- 2. Что сделать? Просмотрите решение примеров По этому образцу выполните примеры для самостоятельного решения. Прислать только решение
- 3. Показательные уравнения. Определение. Уравнения вида: называются показательными уравнениями. Теорема. Показательное уравнение равносильно уравнению f(x)=g(x).
- 4. Показательные уравнения. Пример. Решить уравнение: а) б) в) Решение. а) Мы хорошо знаем Перепишем наше уравнение:
- 5. Показательные уравнения. Пример. Решить уравнение Решение: Перепишем наше уравнение: Давайте сделаем замену переменных пусть В новых
- 6. Показательные уравнения. Давайте составим памятку способов решения показательных уравнений: 1. Графический метод. Представляем обе части уравнения
- 7. Показательные неравенства. Перейдем к неравенствам, при решение неравенств стоит обратить особое внимание на основание степени, тут
- 8. Показательные неравенства. Пример. Решить неравенство: а) б) в) Решение. а) Наше неравенство равносильно неравенству: Ответ: (0,5;+∞)
- 10. Скачать презентацию







 Разделите выражения на группы
Разделите выражения на группы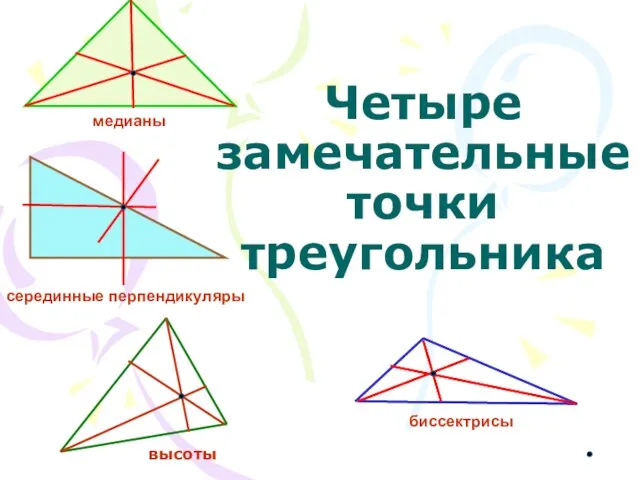 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника В гостях у деда. Аксиомы стереометрии
В гостях у деда. Аксиомы стереометрии Вписанная и описанная окружности
Вписанная и описанная окружности Смежные и вертикальные углы
Смежные и вертикальные углы Математические ребусы
Математические ребусы Многогранники и их основные свойства
Многогранники и их основные свойства Прямоугольные треугольники
Прямоугольные треугольники Презентация на тему График функции (7 класс)
Презентация на тему График функции (7 класс)  Ряды динамики
Ряды динамики Устный счет. Нумерация. Числа, которые больше 1000
Устный счет. Нумерация. Числа, которые больше 1000 Геометрические приложения определенного интеграла
Геометрические приложения определенного интеграла Производная произведения. Производная частного
Производная произведения. Производная частного Презентация на тему Математика и спорт (5 класс)
Презентация на тему Математика и спорт (5 класс)  Математика в медицине
Математика в медицине Презентация на тему Перпендикулярность
Презентация на тему Перпендикулярность  Пирамида – это многогранник, составленный из n-угольника
Пирамида – это многогранник, составленный из n-угольника Презентация на тему Начальные понятия планиметрии. Прямая и отрезок. Луч и угол
Презентация на тему Начальные понятия планиметрии. Прямая и отрезок. Луч и угол  Презентация на тему УРАВНЕНИЕ И ЕГО КОРНИ
Презентация на тему УРАВНЕНИЕ И ЕГО КОРНИ  Многочлен. Основные понятия. Определение многочлена
Многочлен. Основные понятия. Определение многочлена Разложение многочлена на множители
Разложение многочлена на множители Трансформация координат и модели высоты
Трансформация координат и модели высоты Логарифмическая функция, ее свойства и график
Логарифмическая функция, ее свойства и график Первообразная F'(x) = f(x)
Первообразная F'(x) = f(x) Деление обыкновенных дробей
Деление обыкновенных дробей Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения
Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения Стародубцева Анна 9-а класс
Стародубцева Анна 9-а класс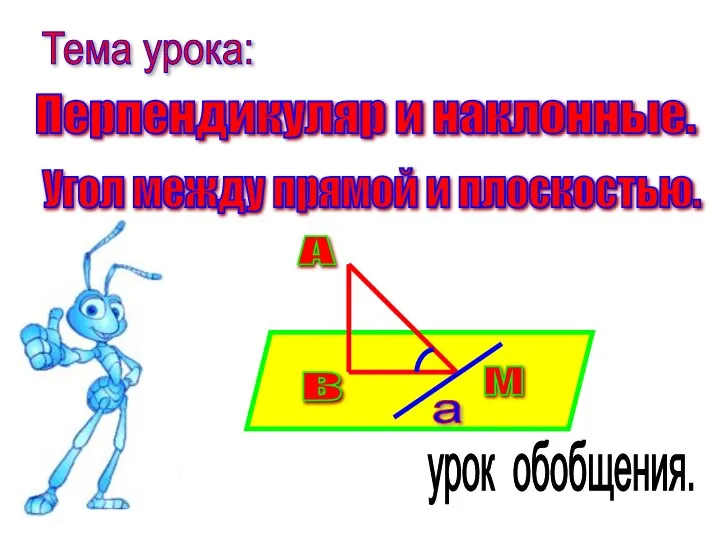 Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр и наклонные. Угол между прямой и плоскостью