векторы

Содержание
I. Понятие вектора в пространстве
II. Коллинеарные векторы
III. Компланарные векторы
IV. Действия с векторами
V. Разложение вектора
VI. Базисные задачи
Проверь себя
Об авторе
Помощь в управлении презентацией
Выход

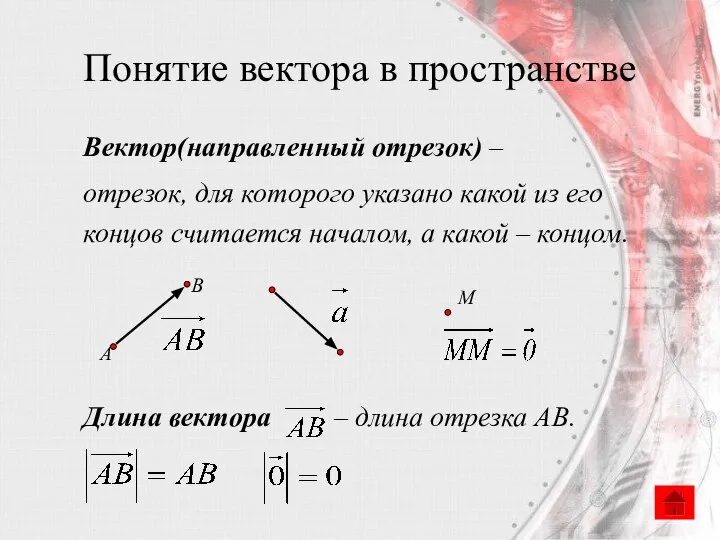
Понятие вектора в пространстве
Вектор(направленный отрезок) –
отрезок, для которого указано какой из его концов считается началом, а какой – концом.
Длина вектора – длина отрезка AB.
А
В
M

Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на одной
прямой или параллельных прямых.
Среди коллинеарных различают:
Сонаправленные векторы
Противоположно направленные векторы

Сонаправленные векторы
Сонаправленные векторы - векторы, лежащие
по одну сторону от прямой, проходящей через их начала.
Нулевой вектор считается сонаправленным с любым вектором.
Равные векторы

Равные векторы
Равные векторы - сонаправленные векторы,
длины которых равны.
От любой точки можно отложить вектор,
равный данному, и притом только один.

Противоположно направленные векторы
Противоположно направленные векторы – векторы, лежащие по разные стороны от прямой, проходящей через их начала.
Противоположные векторы

Противоположные векторы
Противоположные векторы – противоположно направленные векторы, длины которых равны.
Вектором, противоположным нулевому,
считается нулевой вектор.

Признак коллинеарности
Доказательство

Определение компланарных векторов
Компланарные векторы – векторы, при откладывании которых от одной и той же точки пространства, они будут лежать в одной плоскости.
Пример:
B
А
C
D
A1
B1
C1
D1

О компланарных векторах
Любые два вектора всегда компланарны.
Три вектора, среди которых имеются два коллинеарных, компланарны.
α
если

Признак компланарности
Доказательство
Задачи

Свойство компланарных
векторов

Действия с векторами
Сложение
Вычитание
Умножение вектора на число
Скалярное произведение

Сложение векторов
Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
Свойства сложения

Правило треугольника
А
B
C

Правило треугольника
А
B
C
Для любых трех точек А, В и С справедливо равенство:

Правило параллелограмма
А
B
C

Свойства сложения

Правило многоугольника
Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при последовательном откладывании).
B
A
C
D
E
Пример

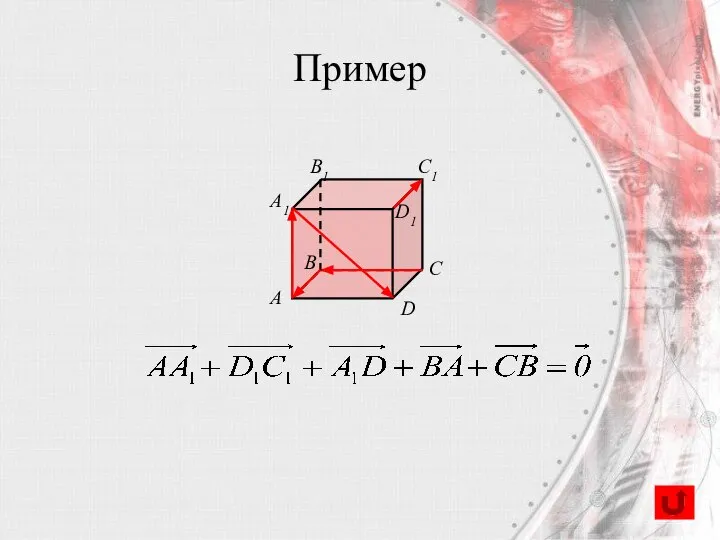
Пример
C
A
B
D
A1
B1
C1
D1

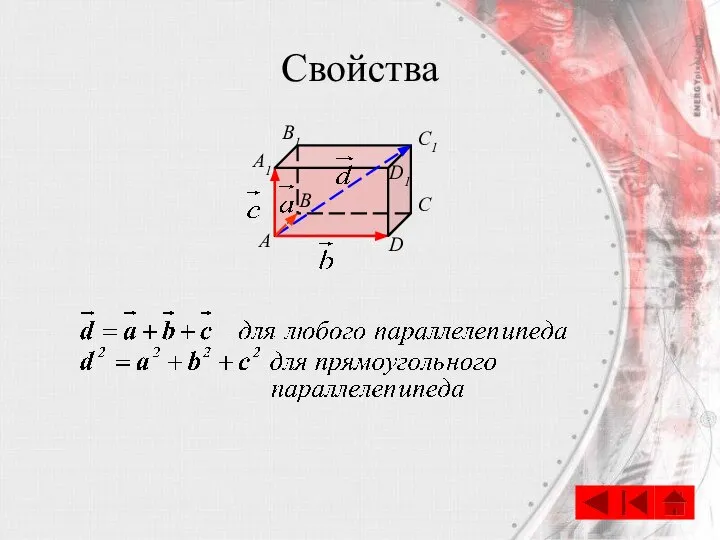
Правило параллелепипеда
B
А
C
D
A1
B1
C1
D1
Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.

Свойства
B
А
C
D
A1
B1
C1
D1

Вычитание векторов
Вычитание
Сложение с противоположным

Вычитание
Разностью векторов и называется такой
вектор, сумма которого с вектором равна
вектору .

Вычитание
B
A
Правило трех точек
C

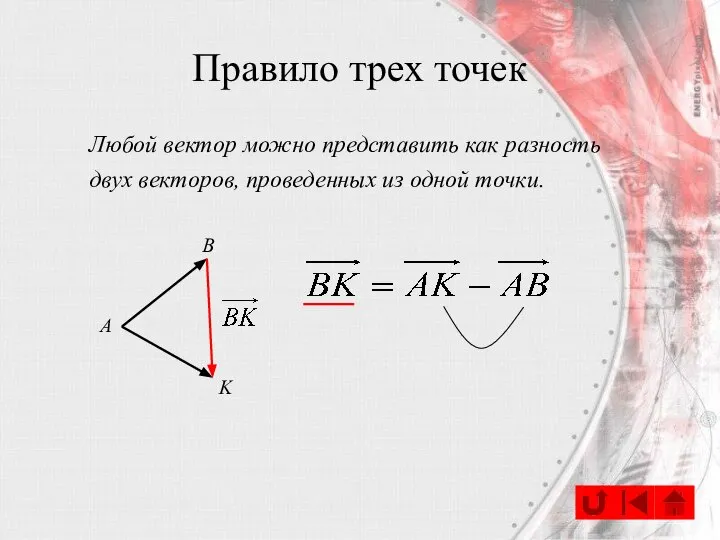
Правило трех точек
Любой вектор можно представить как разность двух векторов, проведенных из одной точки.
А
B
K

Сложение с противоположным
Разность векторов и можно представить как сумму вектора и вектора, противоположного вектору .
А
B
O

Умножение вектора на число

Свойства
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение любого вектора на число нуль есть нулевой вектор.

Свойства

Скалярное произведение
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Справедливые утверждения
Вычисление скалярного произведения в координатах
Свойства скалярного произведения

Справедливые утверждения
скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти векторы перпендикулярны
скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату
его длины

Вычисление скалярного произведения в координатах
Доказательство

Свойства скалярного
произведения
10.
20.
30.
40.
(переместительный закон)
(распределительный закон)
(сочетательный закон)

Разложение вектора
По двум неколлинеарным векторам
По трем некомпланарным векторам

Разложение вектора по двум неколлинеарным векторам
Теорема.
Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Доказательство

Разложение вектора по трем некомпланарным векторам
Если вектор p представлен в виде
где x, y, z – некоторые числа, то говорят, что вектор
разложен по векторам , и .
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Доказательство

Свойства векторного произведения
4.
1.
2.
3.

Вычисление векторного произведения по координатам