Содержание
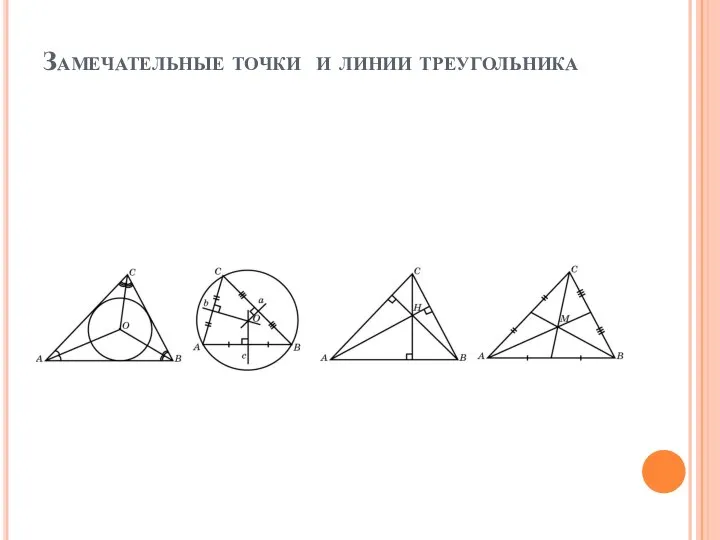
- 2. Замечательные точки и линии треугольника
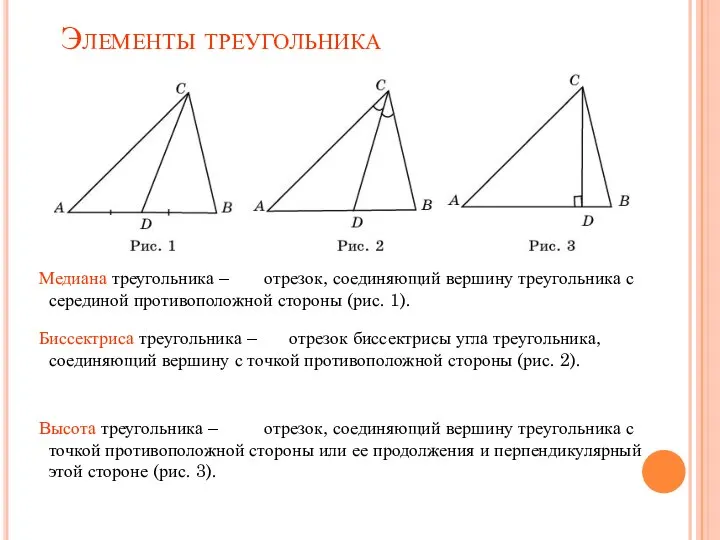
- 3. Элементы треугольника Медиана треугольника – Биссектриса треугольника – Высота треугольника – отрезок, соединяющий вершину треугольника с
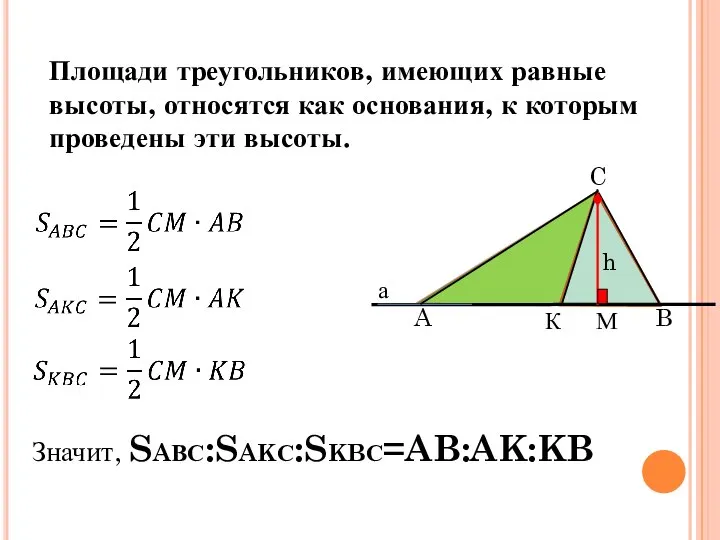
- 4. Значит, SAВС:SAKС:SKBС=AB:AK:KB Пропорциональность площадей Площади треугольников, имеющих равные высоты, относятся как основания, к которым проведены эти
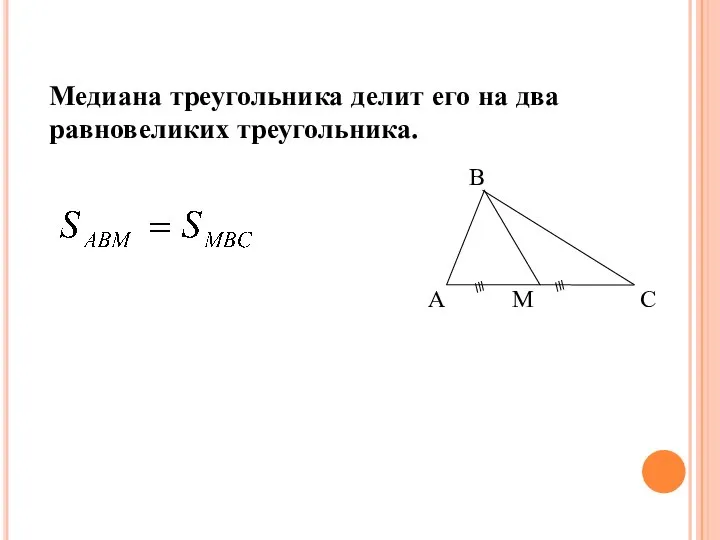
- 5. Медиана треугольника делит его на два равновеликих треугольника. Следствие 1
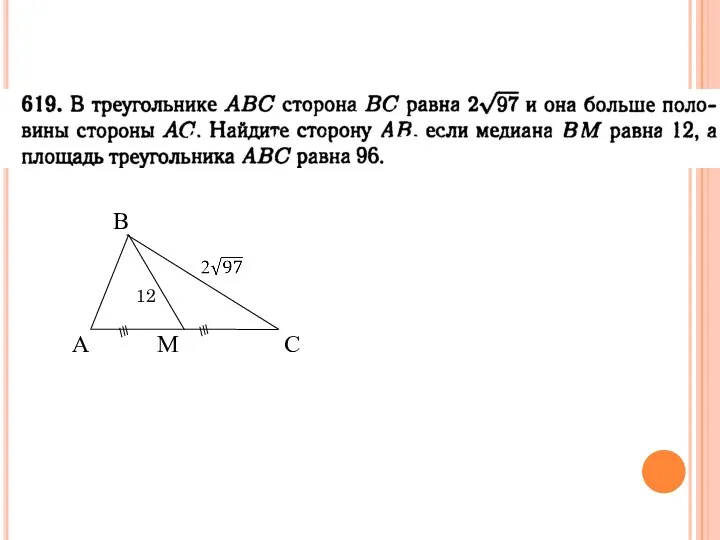
- 6. Применение 12
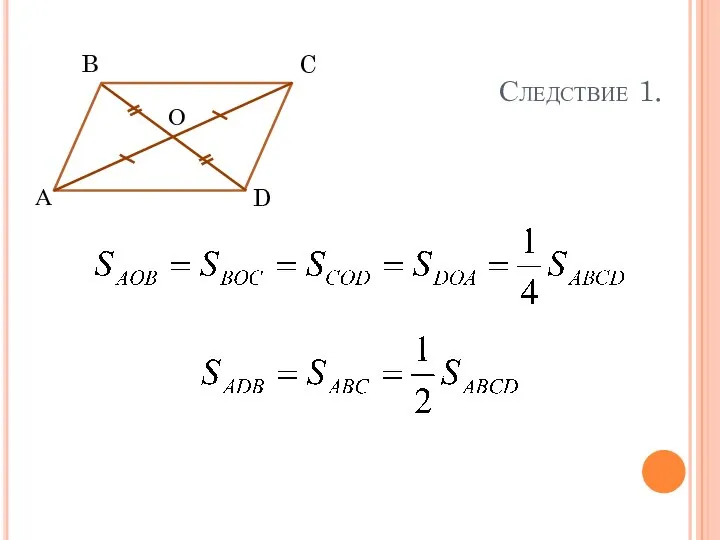
- 7. А B C D О Рассмотреть на уроке Следствие 1.
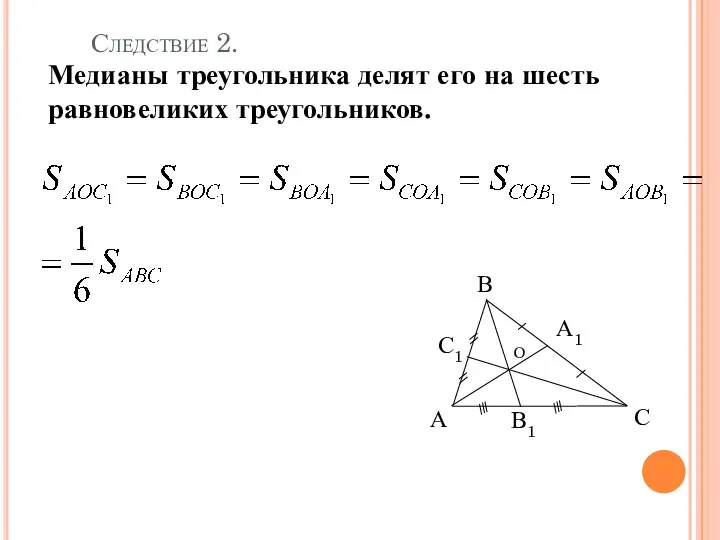
- 8. В Следствие 2 Медианы треугольника делят его на шесть равновеликих треугольников. Следствие 2.
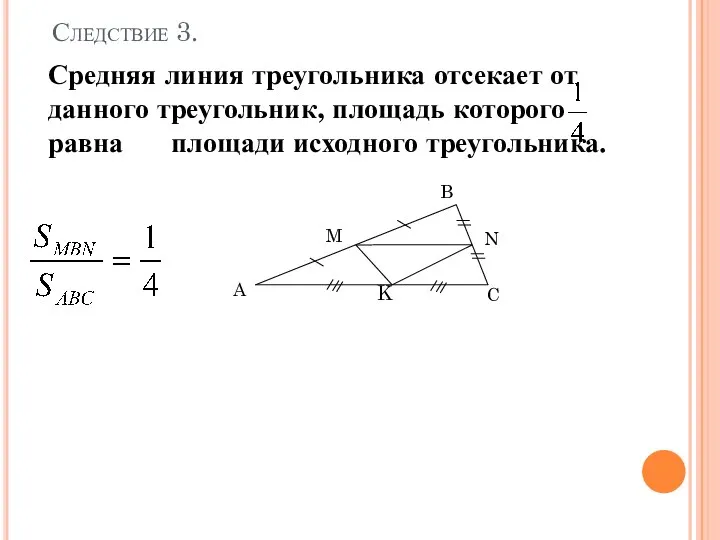
- 9. Доказать на уроке Средняя линия треугольника отсекает от данного треугольник, площадь которого равна площади исходного треугольника.
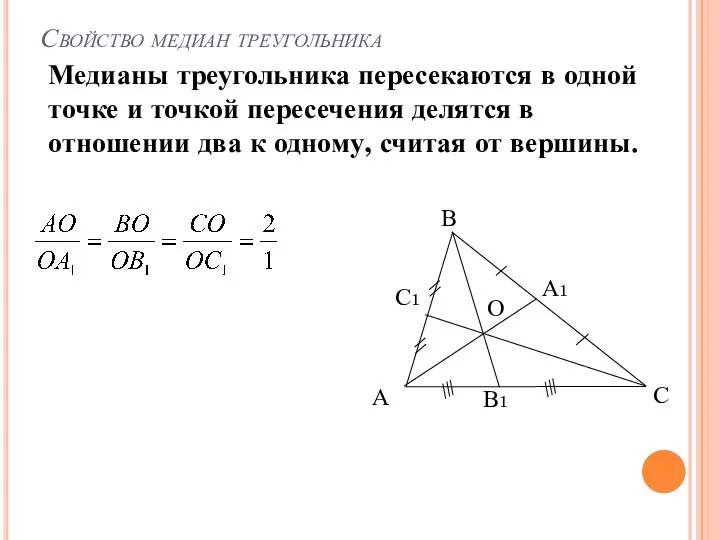
- 10. Теорема Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении два к одному,
- 12. Скачать презентацию
 Пропорции. Задачи
Пропорции. Задачи Презентация на тему Движение
Презентация на тему Движение  Сложение и вычитание числа 2
Сложение и вычитание числа 2 Математика
Математика Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ  Математика и спорт
Математика и спорт Разложение вектора по трём некомпланарным векторам
Разложение вектора по трём некомпланарным векторам Десятки, единицы, цифры
Десятки, единицы, цифры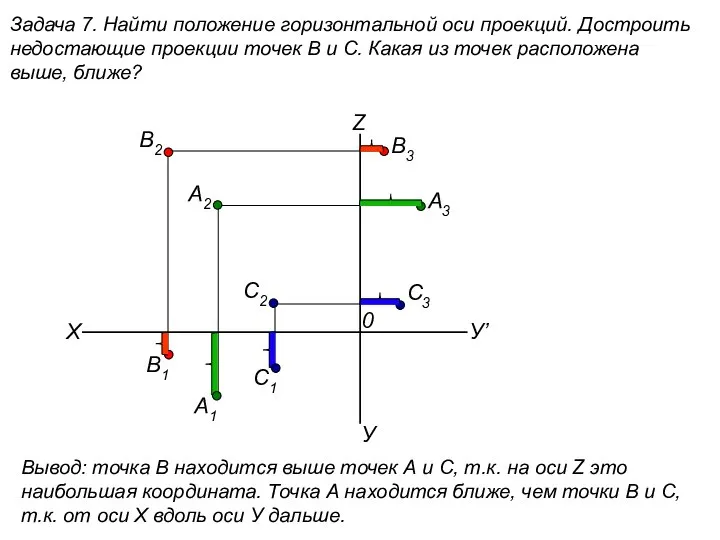 Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7)
Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7) Уравнение касательной к графику функции
Уравнение касательной к графику функции Решение уравнений. Первый и второй уровни
Решение уравнений. Первый и второй уровни Предельные величины, эластичности
Предельные величины, эластичности Математика – наука о наиболее общих и фундаментальных структурах реального мира
Математика – наука о наиболее общих и фундаментальных структурах реального мира Практическое применение треугольников в жизни
Практическое применение треугольников в жизни Освоение основных универсальных предметных знаний и умений в курсе технологии
Освоение основных универсальных предметных знаний и умений в курсе технологии Ряды динамики
Ряды динамики Презентация по математике "Знакомство с занимательной литературой по математике" -
Презентация по математике "Знакомство с занимательной литературой по математике" -  Простейшие функции и их графики
Простейшие функции и их графики Решение тригонометрических уравнений
Решение тригонометрических уравнений Логарифмические уравнения
Логарифмические уравнения Занимательные задачи
Занимательные задачи Комбинаторика
Комбинаторика Площадь параллелограмма. 8 класс
Площадь параллелограмма. 8 класс Соста числа 11
Соста числа 11 Обратные тригонометрические функции
Обратные тригонометрические функции Десятичный и натуральный логарифм
Десятичный и натуральный логарифм Параллельный перенос
Параллельный перенос Геймификация образовательного процесса на уроках математики с использованием двигательной активности
Геймификация образовательного процесса на уроках математики с использованием двигательной активности