объёмов и площадей некоторых тел. В образование геометрии, как науки внесли огромный вклад древнегреческие ученые Фалес, Пифагор, Демокрит, Евклид и другие.
В сочинении Евклида «Начала» были упорядочены известные в то время сведения о геометрии. В «Началах» был развит аксиоматический, состоящий в том, что сначала строились утверждения (аксиомы) , принимаемые без доказательств, а потом на их основе строились иные утверждения (теоремы). Качественно новая геометрия была создана нашим соотечественником Лобачевским, пытавшимся доказать, как теорему постулат Евклида «О параллельных прямых» от противного и, не получив никаких утверждений, противоречащих данному постулату смог построить геометрию, отличную от Евклидовой. Сообщение открытии было сделано в1826 году.
Развитие геометрии

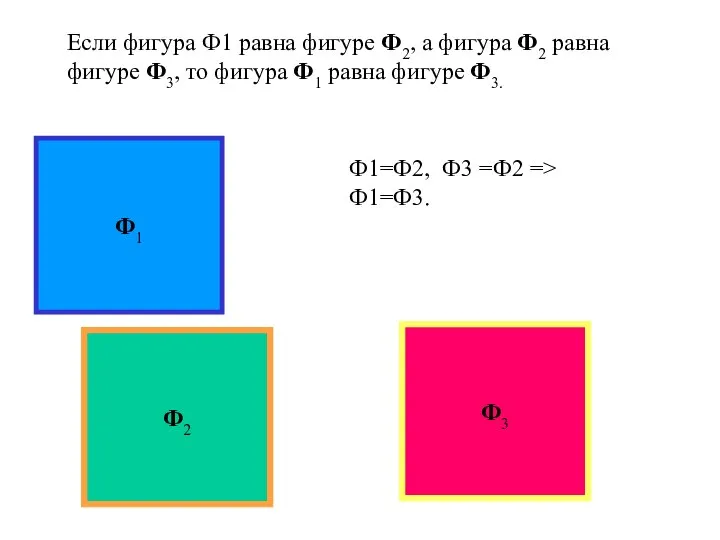
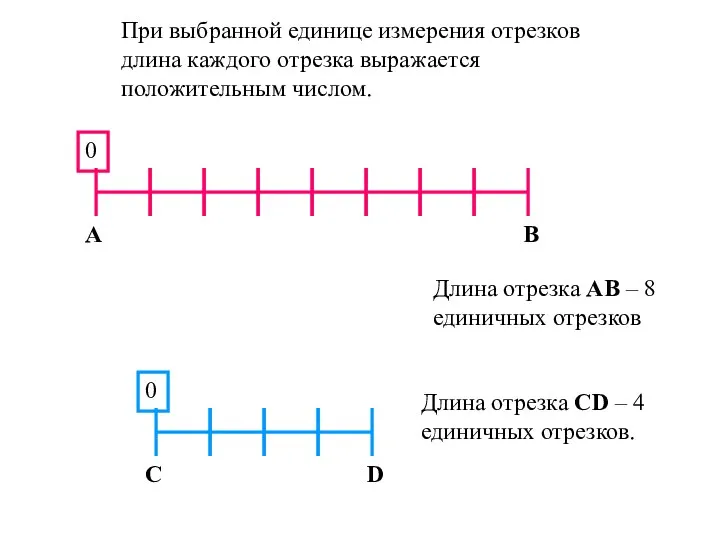
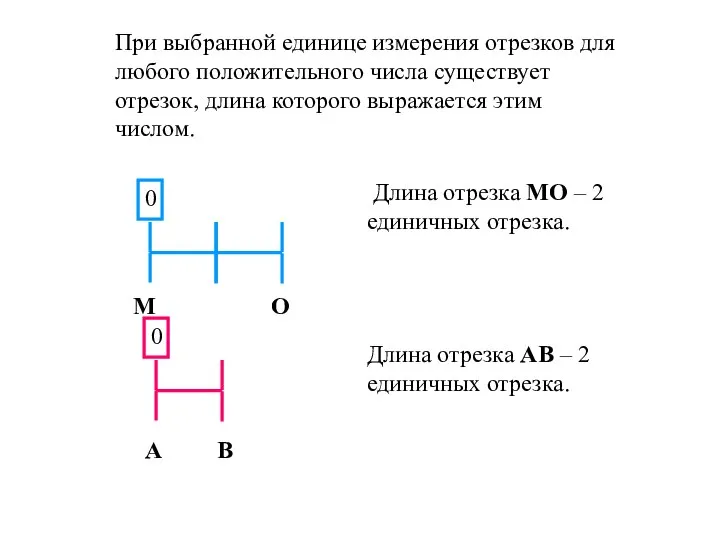
 Презентация на тему Формулы суммы и разности синуса и косинуса
Презентация на тему Формулы суммы и разности синуса и косинуса  Отчет кафедры математики за 2010- 2011 учебный год «Создание организационно- педагогических условий для повышения качества образован
Отчет кафедры математики за 2010- 2011 учебный год «Создание организационно- педагогических условий для повышения качества образован Тела вращения
Тела вращения Построение сечений тетраэдра
Построение сечений тетраэдра Логарифмические уравнения. Основные методы их решения
Логарифмические уравнения. Основные методы их решения Понятие квадратных уравнений
Понятие квадратных уравнений Решение задач с помощью рациональных уравнений. 8 класс
Решение задач с помощью рациональных уравнений. 8 класс Презентация на тему Вычитание
Презентация на тему Вычитание  Решение заданий типа № 21 ОГЭ
Решение заданий типа № 21 ОГЭ Сложение и вычитание в пределах 20. 1 класс
Сложение и вычитание в пределах 20. 1 класс Параллельные прямые
Параллельные прямые Тренажёр по математике для 3 класса
Тренажёр по математике для 3 класса Презентация на тему Делимость чисел
Презентация на тему Делимость чисел  Презентация на тему Формирование и развитие УУД на уроках математики
Презентация на тему Формирование и развитие УУД на уроках математики  Самостоятельная работа по теме Векторы
Самостоятельная работа по теме Векторы Задачи В Детском мире
Задачи В Детском мире Пропорции
Пропорции Мастер-класс по математике. Где нас ждут?
Мастер-класс по математике. Где нас ждут?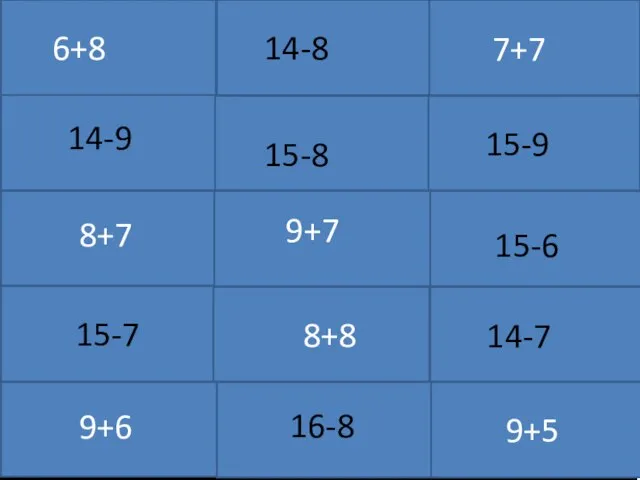 Примеры карточек. Счет +-10 11 12 13 14 15 16
Примеры карточек. Счет +-10 11 12 13 14 15 16 Нумерология. Пифагор
Нумерология. Пифагор Площадь прямоугольника. Урок-открытие. 2 класс
Площадь прямоугольника. Урок-открытие. 2 класс Квадратные уравнения. Анаграммы
Квадратные уравнения. Анаграммы Математическое моделирование многокомпонентной ректификации. Коммерческие симуляторы
Математическое моделирование многокомпонентной ректификации. Коммерческие симуляторы Первый признак равенства треугольников
Первый признак равенства треугольников Оптимізація процесів прийняття рішень при плануванні транспортних перевезень в умовах невизначеності
Оптимізація процесів прийняття рішень при плануванні транспортних перевезень в умовах невизначеності Теория массового обслуживания
Теория массового обслуживания Вычисление окружности
Вычисление окружности Predel_funktsii_v_tochke
Predel_funktsii_v_tochke