Содержание
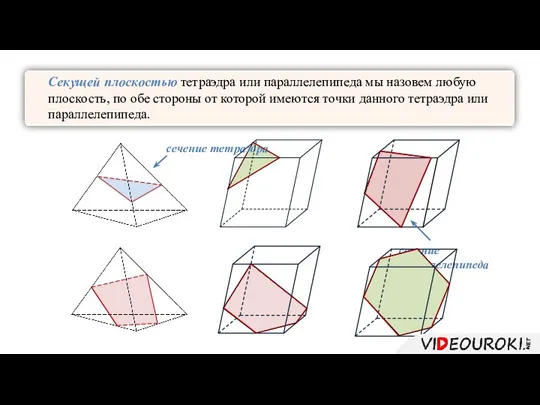
- 4. Секущей плоскостью тетраэдра или параллелепипеда мы назовем любую плоскость, по обе стороны от которой имеются точки
- 5. Секущей плоскостью тетраэдра или параллелепипеда мы назовем любую плоскость, по обе стороны от которой имеются точки
- 6. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
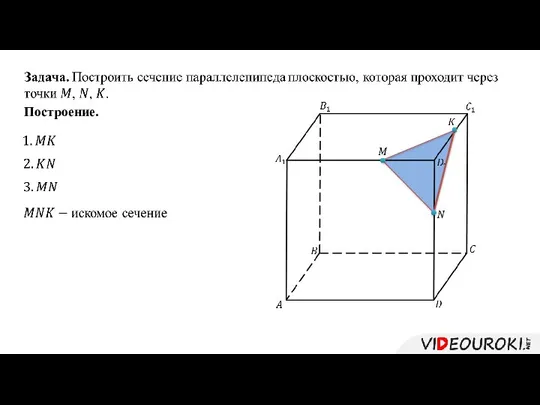
- 7. Построение.
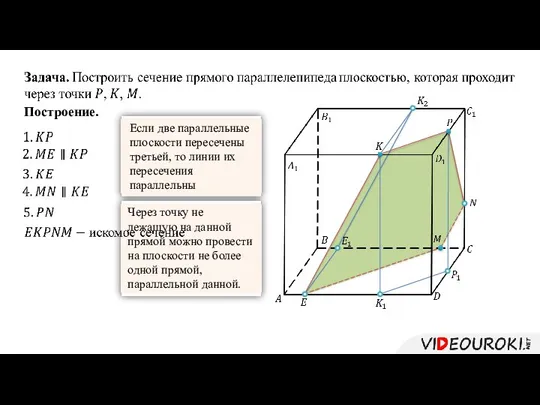
- 8. Построение.
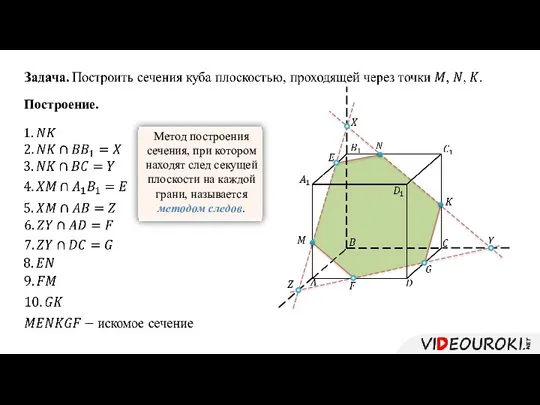
- 9. Построение.
- 10. Построение.
- 11. Построение. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны Через точку не лежащую
- 12. Построение. Метод построения сечения, при котором находят след секущей плоскости на каждой грани, называется методом следов.
- 14. Скачать презентацию







 Симметрия в пространстве
Симметрия в пространстве Оптимизация по методу Бокса-Уилсона
Оптимизация по методу Бокса-Уилсона Прямоугольник. Теоремы
Прямоугольник. Теоремы Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Умножение десятичной дроби на единицу с нулями
Умножение десятичной дроби на единицу с нулями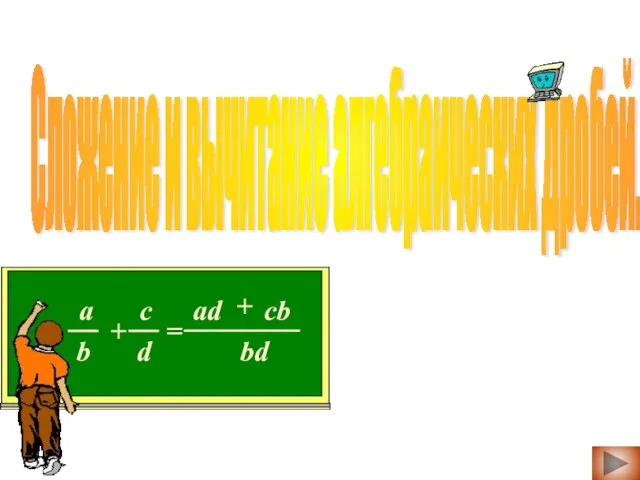 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей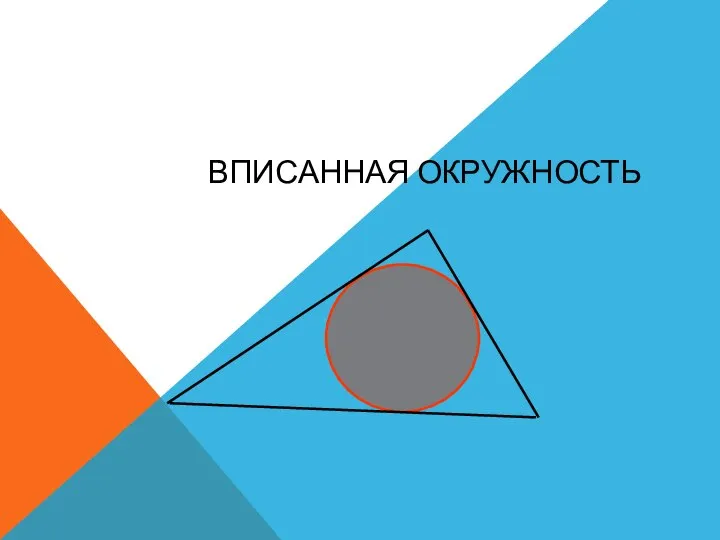 Вписанная окружность
Вписанная окружность Многогранники. Стереометрия
Многогранники. Стереометрия Правильный многоугольник
Правильный многоугольник Окружность и круг
Окружность и круг Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Задачи на умножение
Задачи на умножение Случайные величины
Случайные величины Равенство векторов
Равенство векторов Графы
Графы Экономический факторный анализ. Теорема о среднем
Экономический факторный анализ. Теорема о среднем Счет до 10
Счет до 10 Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Упражнения
Упражнения Состав чисел в приделах 10. Закрепление изученного материала
Состав чисел в приделах 10. Закрепление изученного материала Решение задач на нахождение зависимости между величинами используя графики
Решение задач на нахождение зависимости между величинами используя графики График функции
График функции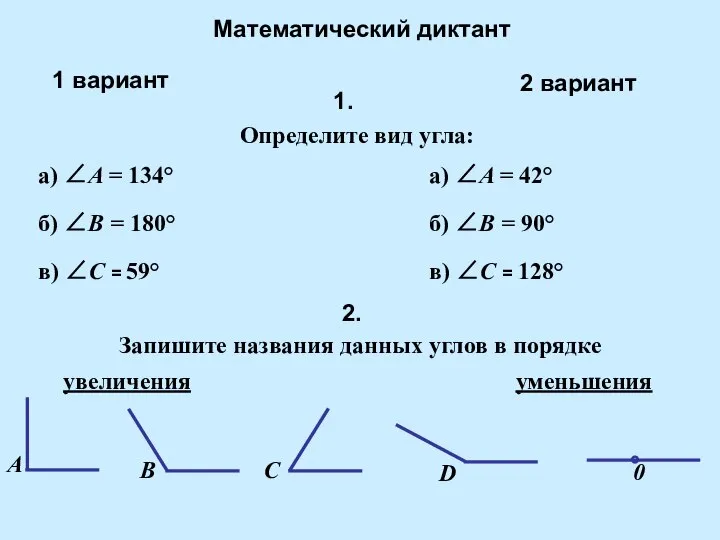 Математический диктант
Математический диктант Применение векторов к решению задач (9 класс)
Применение векторов к решению задач (9 класс) Метод рационализации в логарифмических неравенствах
Метод рационализации в логарифмических неравенствах Numbers and animals
Numbers and animals Свойства функций
Свойства функций Умножение обыкновенных дробей
Умножение обыкновенных дробей