Площадь треугольника и подобие

Замечательные точки и линии треугольника

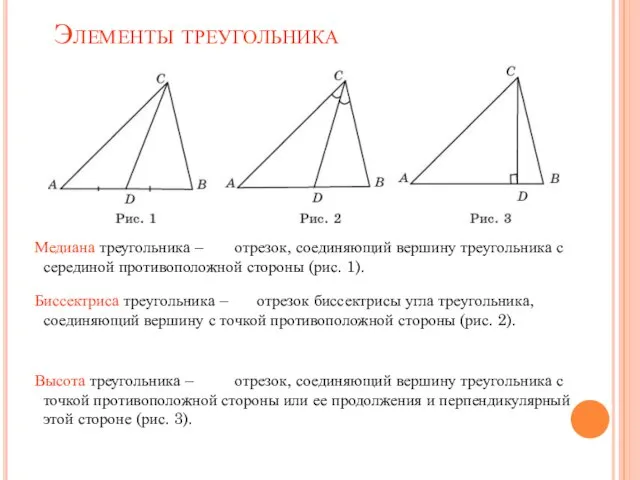
Элементы треугольника
Медиана треугольника –
Биссектриса треугольника –
Высота треугольника –
отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис. 1).
отрезок биссектрисы угла треугольника, соединяющий вершину с точкой противоположной стороны (рис. 2).
отрезок, соединяющий вершину треугольника с точкой противоположной стороны или ее продолжения и перпендикулярный этой стороне (рис. 3).

Значит, SAВС:SAKС:SKBС=AB:AK:KB
Пропорциональность площадей
Площади треугольников, имеющих равные высоты, относятся как основания, к которым проведены эти высоты.

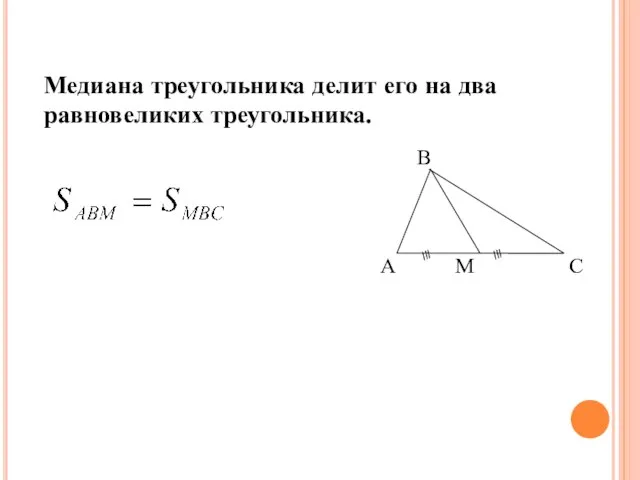
Медиана треугольника делит его на два равновеликих треугольника.
Следствие 1

А
B
C
D
О
Рассмотреть на уроке
Следствие 1.

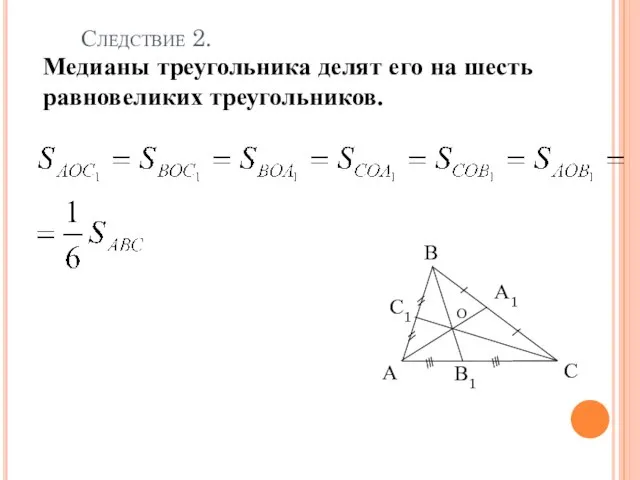
В
Следствие 2
Медианы треугольника делят его на шесть равновеликих треугольников.
Следствие 2.

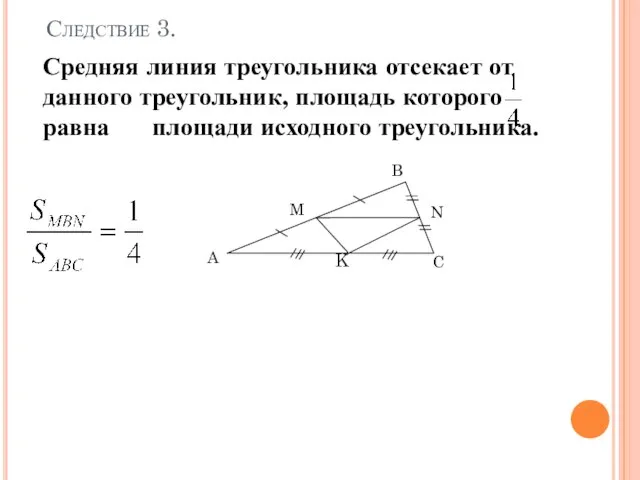
Доказать на уроке
Средняя линия треугольника отсекает от данного треугольник, площадь которого равна площади исходного треугольника.
Следствие 3.

Подобие треугольников

Вспомнить доказанное ранее
Площади треугольников
АВО и DCO равны.

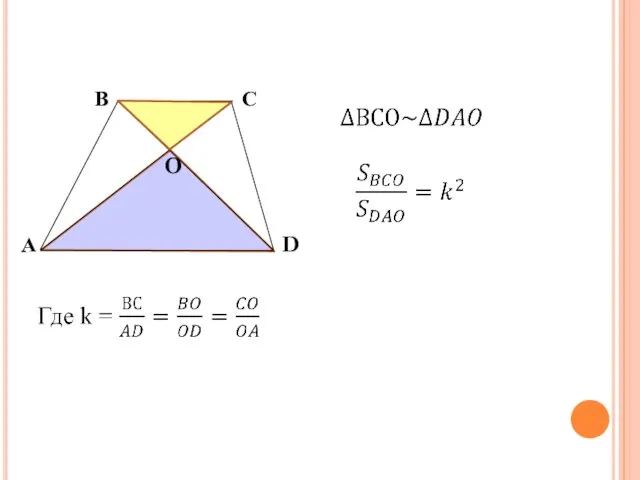
Диагонали AC и BD трапеции ABCD пересекаются в точке O. Площади треугольников AOD и BOC равны соответственно 16 и 9. Найдите площадь трапеции.
ГИА 2012

Решение
k² = 9/16 = > k= ¾ => ОС:ОА =
=3:4 = > SОСВ : SОАВ = 3:4= > SОАВ = 9:3·4 = 12.
SОСD = SОАВ =12.
SABCD = SОСВ + SОАD + SОСD +SОАВ = =9+16+24=49.

Задачи для самостоятельного решения.
1) Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая, пересекающая сторону ВС в точке Р. Найти отношение площади треугольника АВК и площади четырехугольника КРСМ.
2) В трапеции АВСD отношение длин оснований АD и ВС равно 3. Диагонали трапеции пересекаются в точке О, площадь треугольника АОВ равна 6. Найти площадь трапеции.

ЕГЭ прошлых лет