Содержание
- 2. м е д и а н а Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой
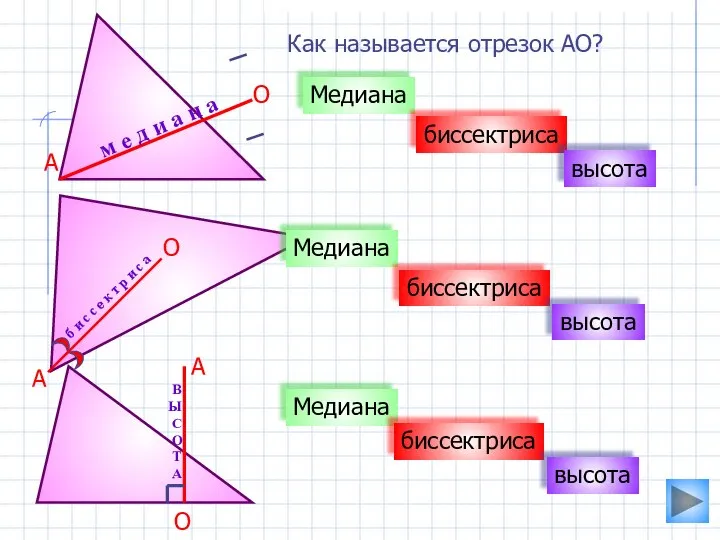
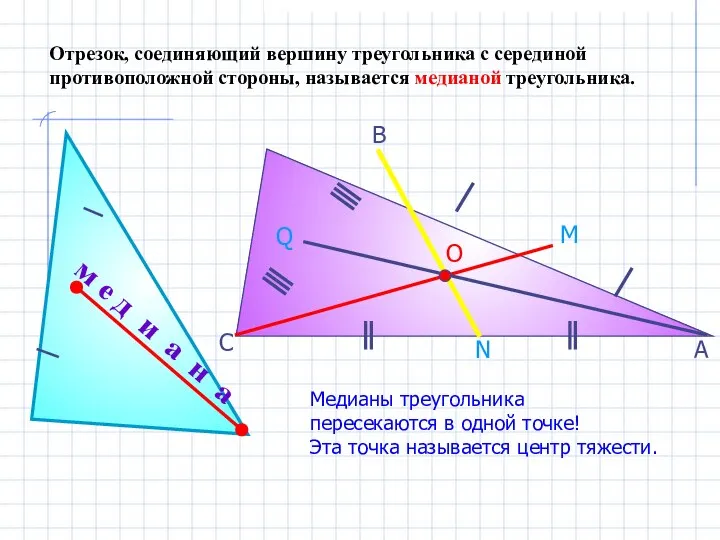
- 3. Как называется отрезок АО? Медиана биссектриса высота м е д и а н а Медиана Медиана
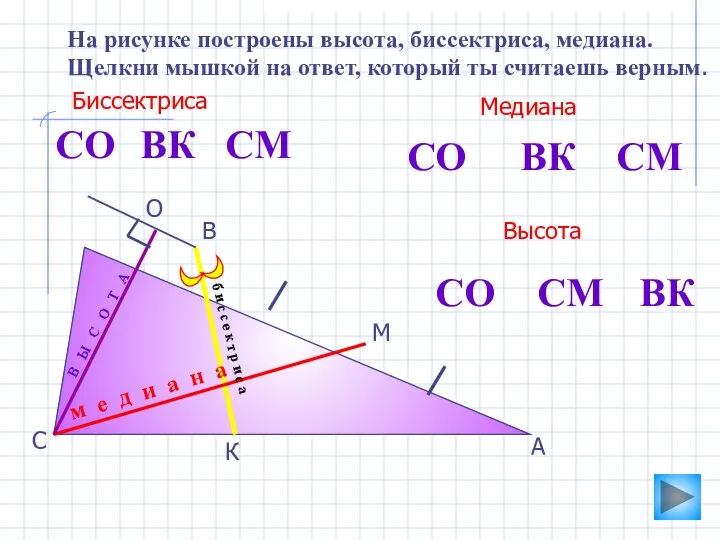
- 4. О А В С К М На рисунке построены высота, биссектриса, медиана. Щелкни мышкой на ответ,
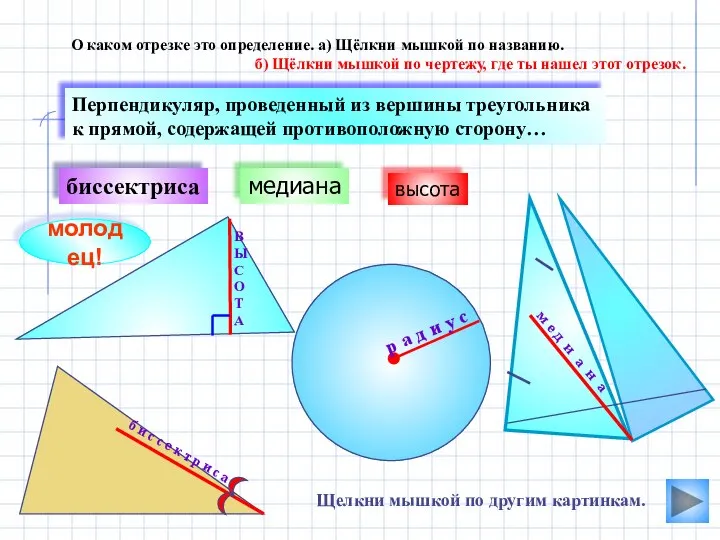
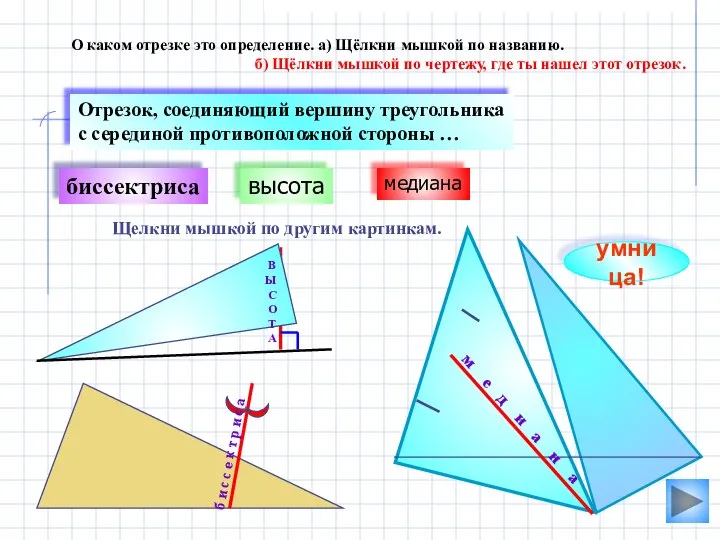
- 5. В Ы С О Т А медиана биссектриса О каком отрезке это определение. а) Щёлкни мышкой
- 6. высота биссектриса О каком отрезке это определение. а) Щёлкни мышкой по названию. б) Щёлкни мышкой по
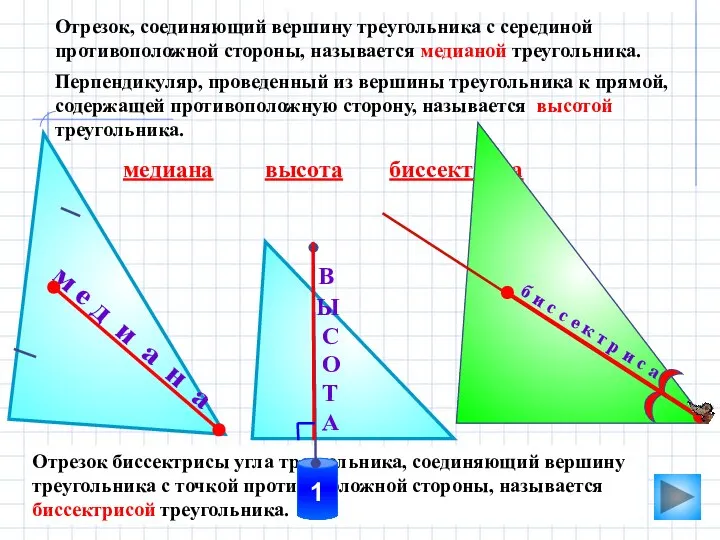
- 7. м е д и а н а Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется
- 8. Треугольник, который опирается на опору по линии медианы, находится в равновесии. Треугольник, который опирается на острие
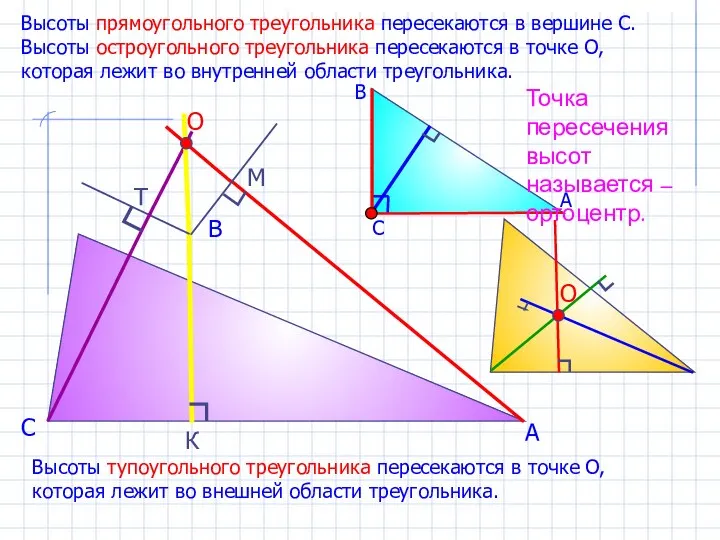
- 9. А В С К М Т Высоты тупоугольного треугольника пересекаются в точке О, которая лежит во
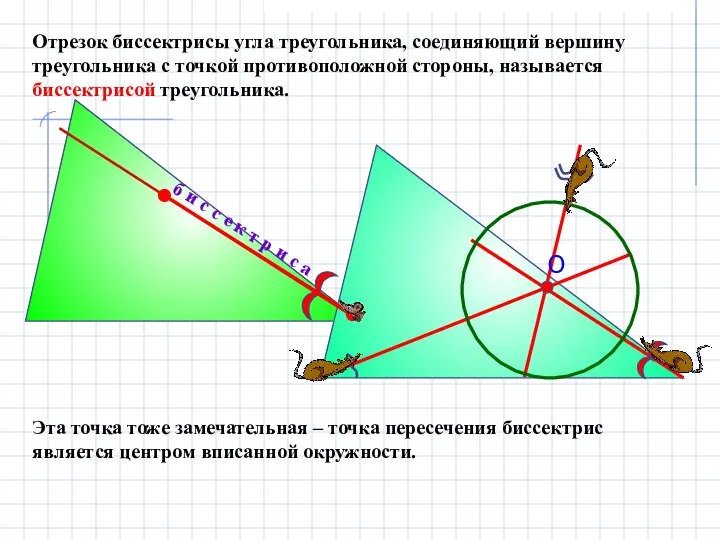
- 10. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. Эта точка
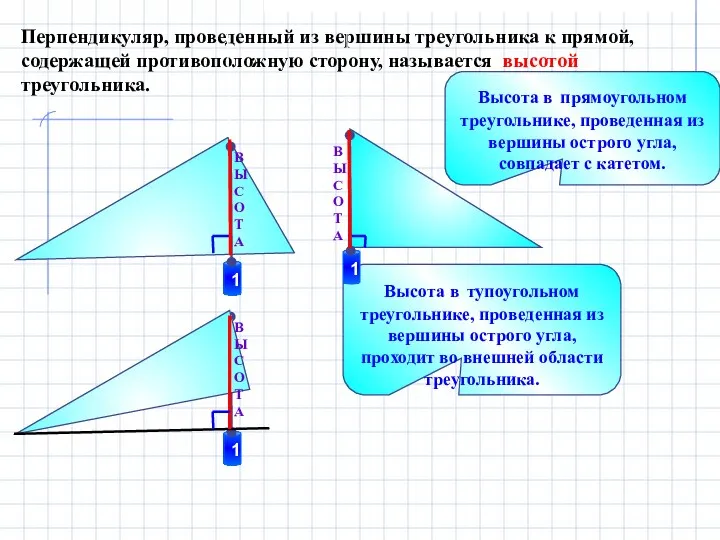
- 11. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника. В Ы С
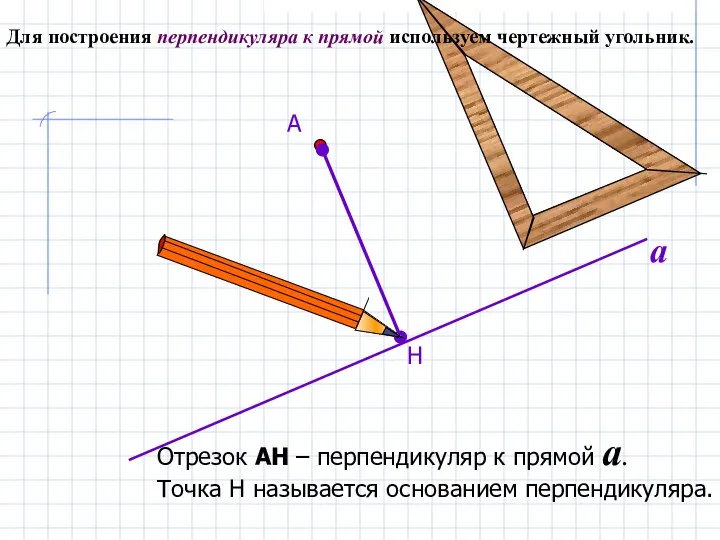
- 12. Для построения перпендикуляра к прямой используем чертежный угольник. Н А Отрезок АН – перпендикуляр к прямой
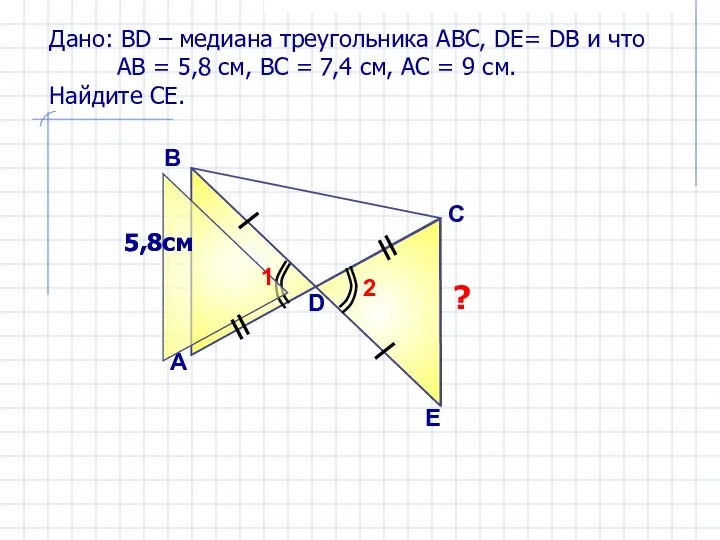
- 13. Дано: ВD – медиана треугольника АВС, DE= DB и что АВ = 5,8 см, ВС =
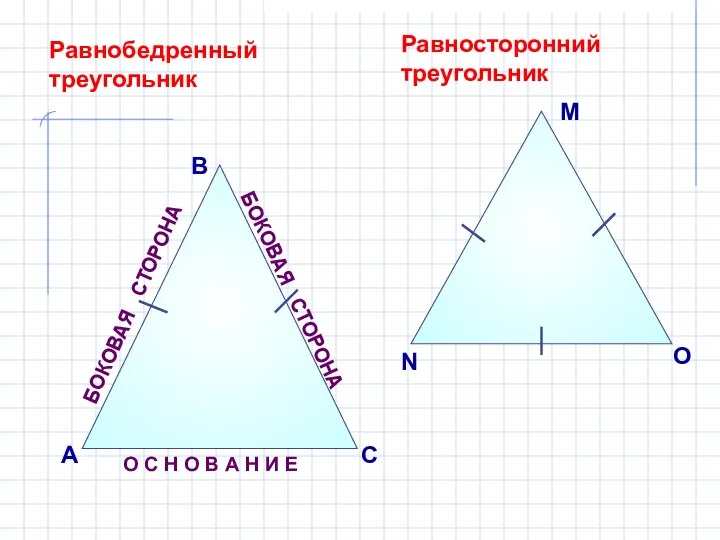
- 14. БОКОВАЯ СТОРОНА В А С Равнобедренный треугольник О С Н О В А Н И Е
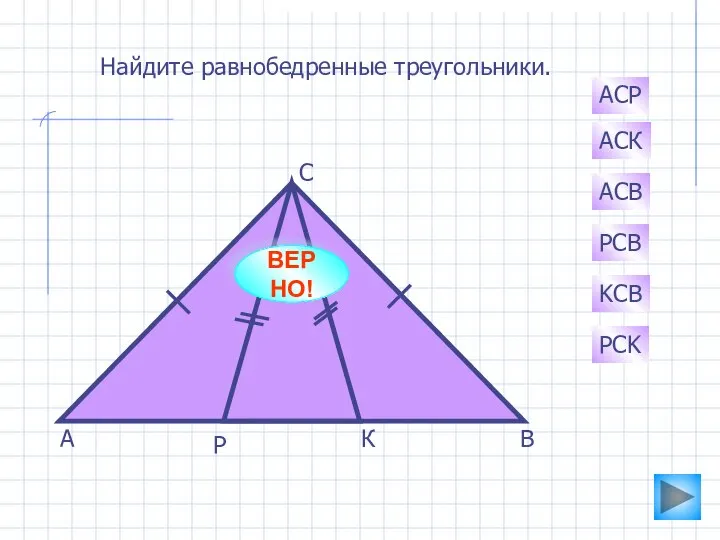
- 15. А К Р С В АСК PCB АСВ АСР KCB PCK Найдите равнобедренные треугольники. ВЕРНО!
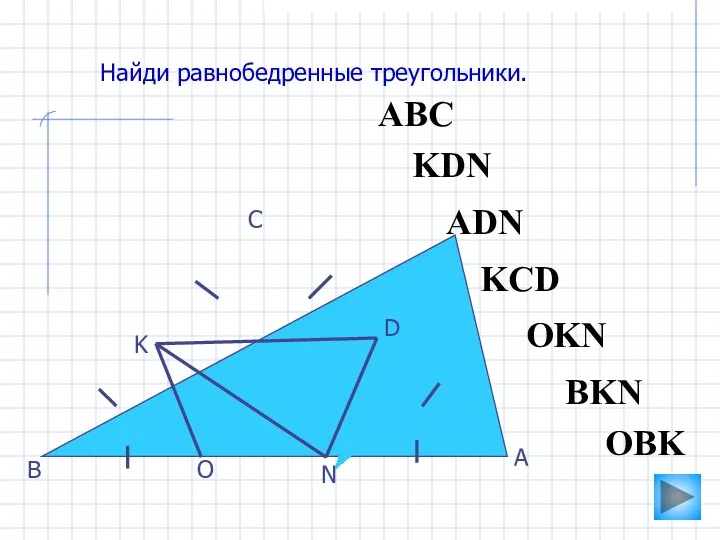
- 16. АВС O N K D С В А Найди равнобедренные треугольники. ADN OBK KCD KDN BKN
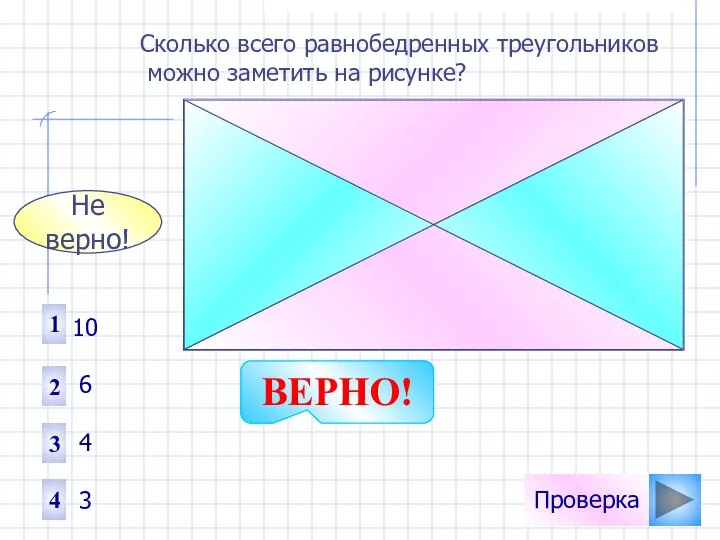
- 17. Проверка Сколько всего равнобедренных треугольников можно заметить на рисунке? 1 2 4 3 10 6 4
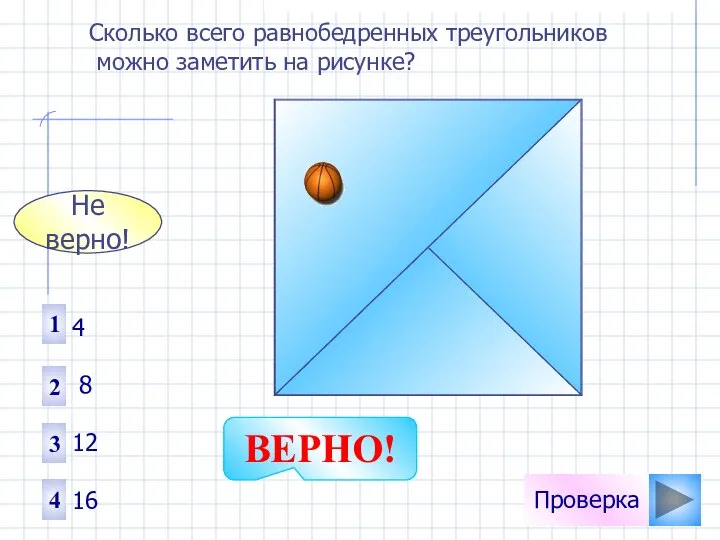
- 18. Проверка Сколько всего равнобедренных треугольников можно заметить на рисунке? 1 2 3 4 4 8 12
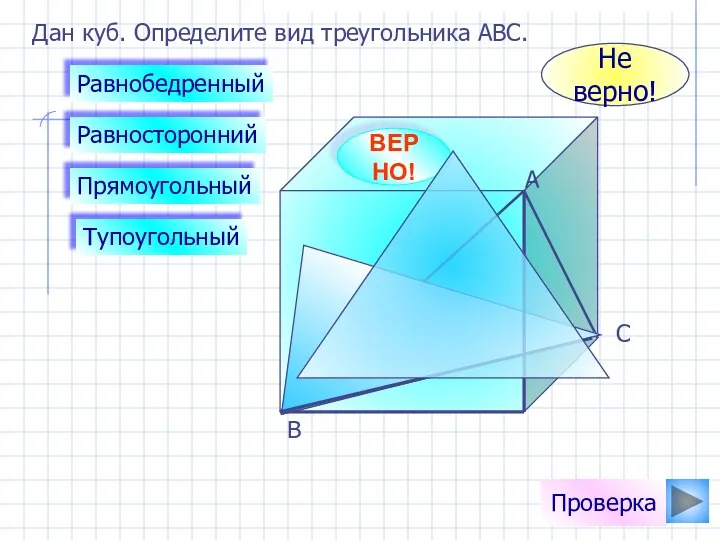
- 19. Дан куб. Определите вид треугольника АВС. Равнобедренный Прямоугольный Равносторонний Тупоугольный ВЕРНО! Не верно! Проверка А В
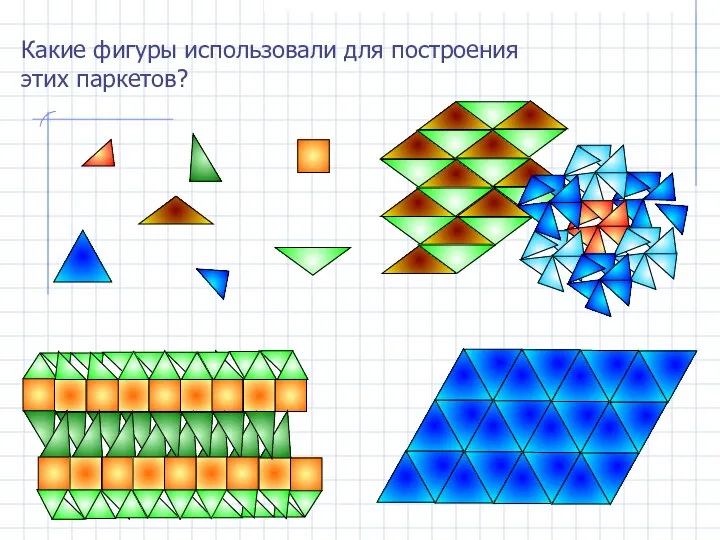
- 20. Какие фигуры использовали для построения этих паркетов?
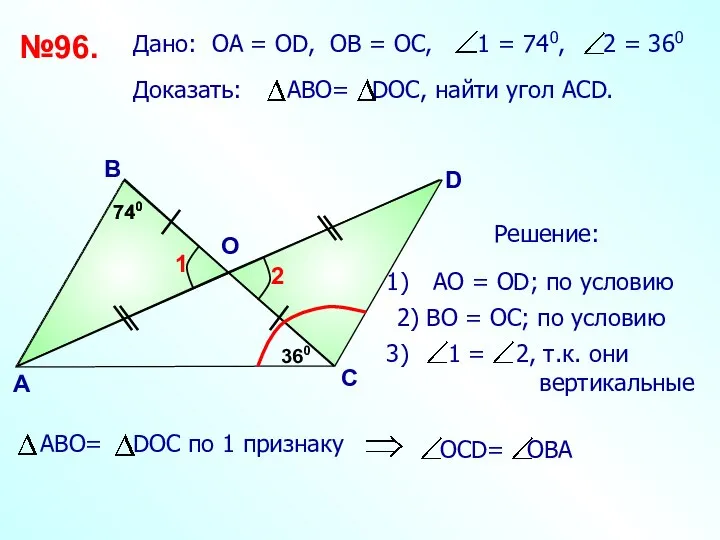
- 21. А D C №96. B 740 360 О АО = ОD; по условию 2) ВО =
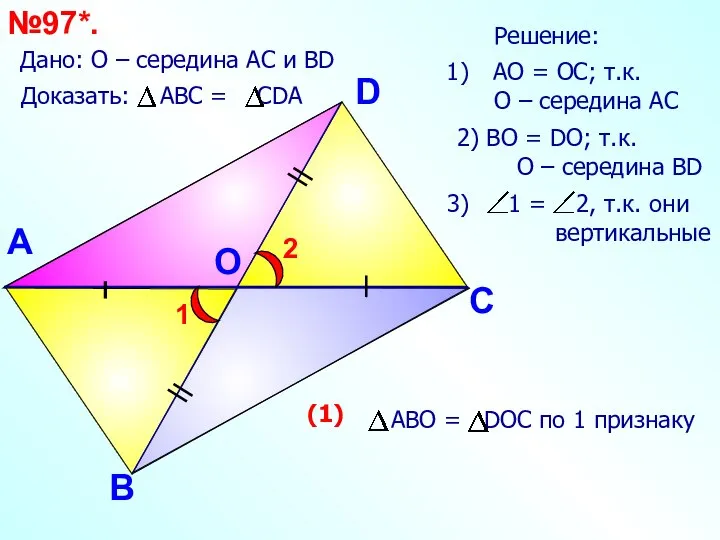
- 22. A O D С В №97*. Дано: О – середина АС и ВD АО = ОC;
- 24. Скачать презентацию

 Ромбическая изометрия. Определение координат
Ромбическая изометрия. Определение координат Решение задач
Решение задач Функции и их графики
Функции и их графики Число Пи
Число Пи Стереометрия. Подготовка к ЕГЭ, задание В11
Стереометрия. Подготовка к ЕГЭ, задание В11 Математика в моей семье
Математика в моей семье Квадратные корни. Квадратные уравнения. 9 класс
Квадратные корни. Квадратные уравнения. 9 класс Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Презентация на тему Окружность
Презентация на тему Окружность  Виды задач на движение
Виды задач на движение Решение простейших тригонометрических уравнений с помощью числовой окружности
Решение простейших тригонометрических уравнений с помощью числовой окружности Окружность
Окружность Действия с десятичными дробями
Действия с десятичными дробями Правильные многоугольники
Правильные многоугольники Парабола и ее свойства
Парабола и ее свойства Презентация на тему Пропорции
Презентация на тему Пропорции  Операции с вероятностями по электроснабжению (задачи)
Операции с вероятностями по электроснабжению (задачи) Первый признак подобия треугольников
Первый признак подобия треугольников Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Задачи на призму
Задачи на призму Презентация на тему ЗАДАНИЯ С РАЗВЕРНУТЫМ ОТВЕТОМ ПОВЫШЕННОГО УРОВНЯ СЛОЖНОСТИ С5. ПОДГОТОВКА К ЕГЭ
Презентация на тему ЗАДАНИЯ С РАЗВЕРНУТЫМ ОТВЕТОМ ПОВЫШЕННОГО УРОВНЯ СЛОЖНОСТИ С5. ПОДГОТОВКА К ЕГЭ  Решение квадратных уравнений выделением квадрата двучлена
Решение квадратных уравнений выделением квадрата двучлена Задачи по геометрии
Задачи по геометрии Презентация на тему Луч и угол (7 класс)
Презентация на тему Луч и угол (7 класс)  Доказательство клауз. Лекция 7
Доказательство клауз. Лекция 7 Золотое сечение и гармония форм природы и искусства. 8 класс
Золотое сечение и гармония форм природы и искусства. 8 класс Устные вычисления. Сравнение текстов задач
Устные вычисления. Сравнение текстов задач Памятки по математике
Памятки по математике