Задачи на проценты

Задание 1. Установите соответствие

100% = 1 10% = 1/10
50% = ½ 5% = 1/20
25% = 1/4 200% = 2
1% = 1/100
Сокращенные процентные соотношения

Основные задачи на проценты
р % = 0,01р = р/100
1. Нахождение процентов данного числа.
Чтобы найти р % от а, надо а·0,01р
2. Нахождение числа по его процентам.
Если известно, что р% числа равно b,
то а = b: 0,01р
3. Нахождение процентного отношения чисел.
Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100%
а/b ·100

Задание 2. Произвести расчеты
1. Найти 25% от 56 14
2. Сколько % составит 30 от 75? 40
Какое число, увеличенное на 13%
составит 339? 300
3.Найдите число, 20% которого равны 12 60
5. На сколько % число 150 больше числа 120?
25
6.В магазине А цену на товары сначала увеличили на 30%, а затем снизили на 30%. В магазине Б –снизили на 30% , затем увеличили на 30%. Где выгодно совершить покупку? А = Б

Задача 1.
При оплате услуг через платежный терминал взымается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
Решение: 300 · 0,05= 15 р – комиссия
300+15 = 315
320 надо положить на счет

Задача 2.
На покупку планшета взяли кредит 20000 р на 1 год под 16 % годовых . Вычислите, сколько денег необходимо вернуть банку, какова ежемесячная сумма выплат?
Решение : 20000*0,16 = 3200 – проценты
20000 + 3200 = 23200 р вся сумма выплат
23200:12= 1933 р за 1 месяц

Задача 3.
Мобильный телефон стоил 5000 рублей. Через некоторое время цену на эту модель снизили до 3000 рублей. На сколько процентов была снижена цена?
Решение:
5000 – 3000 = 2000 – на столько снижена цена на телефон
2000: 5000 ·100 = 2:5 ·100 = 0,4 ·100 = 40 %
Ответ : на 40 %.

Задачи на смеси и сплавы

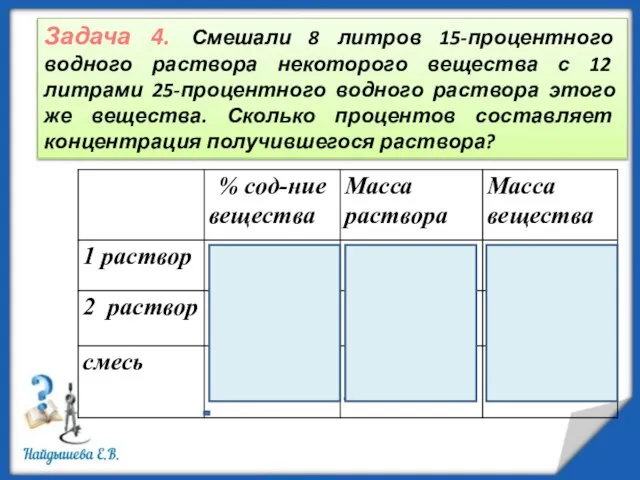
Задача 4. Смешали 8 литров 15-процентного водного раствора некоторого вещества с 12 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

20 x = 8 · 0,15 + 12 · 0,25
20 x = 1,2 + 3 = 4, 2
x = 4,2 : 20 = 0,21 = 21 %
Ответ : 21 %.

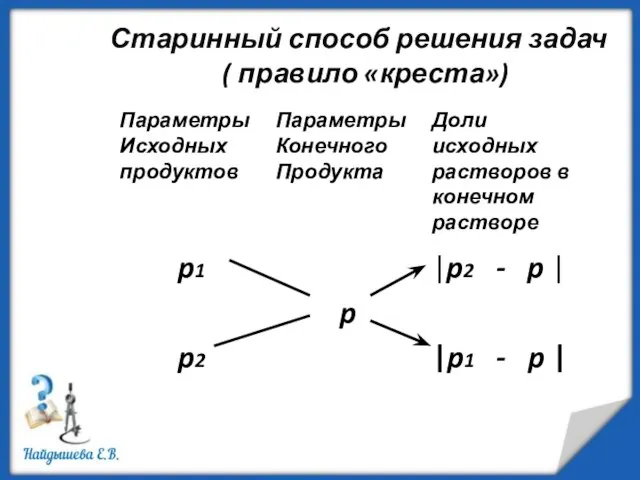
Старинный способ решения задач
( правило «креста»)

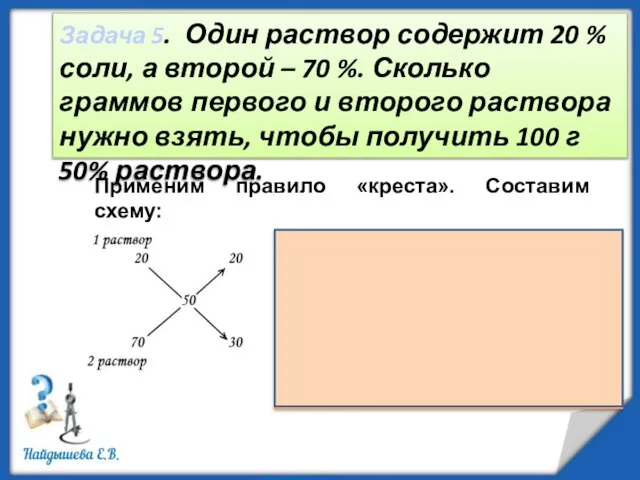
Задача 5. Один раствор содержит 20 % соли, а второй – 70 %. Сколько граммов первого и второго раствора нужно взять, чтобы получить 100 г 50% раствора.
.
100 г смеси составляют 20 + 30 = 50 частей.
100 : ( 20 + 30 ) = 2 г - на 1 часть.
2 ∙ 20 = 40 г – 20% раствора
2 ∙ 30 = 60 г – 70 % раствора
Ответ: 40 г- 20 % раствора; 60 г- 70 % раствора
Применим правило «креста». Составим схему:

Задача 6. Первый сплав содержит 10 % меди, второй - 25 % меди. Из этих двух сплавов получили третий сплав массой 30 кг, содержащий 20 % меди. Какое количество каждого сплава было использовано?
Решить с помощью системы
Решить с помощью уравнения
Решить с помощью «креста»

х ∙ 0,1 + у ∙ 0,25 = 3 * 0,2
х + у = 30
( 3 – у ) ∙ 0,1 + у ∙ 0,25 = 0,6
0,15 у = 0,3
у = 2 , значит х = 1.
Ответ : 1 сплав – 1 кг, 2 сплав – 2 кг.
( 3 – у ) ∙ 0,1 + у ∙ 0,25 = 0,6
х = 3 - у

х ∙ 0,1 + ( 3 - х ) ∙ 0,25 = 3 ∙ 0,2
х ∙ 0,1 + 0,75 - х ∙ 0,25 = 0,6
- 0,15 х = - 0,15
х = 1, значит 3 – 1 = 2.
Ответ: 1 сплав – 1 кг, 2 сплав – 2 кг

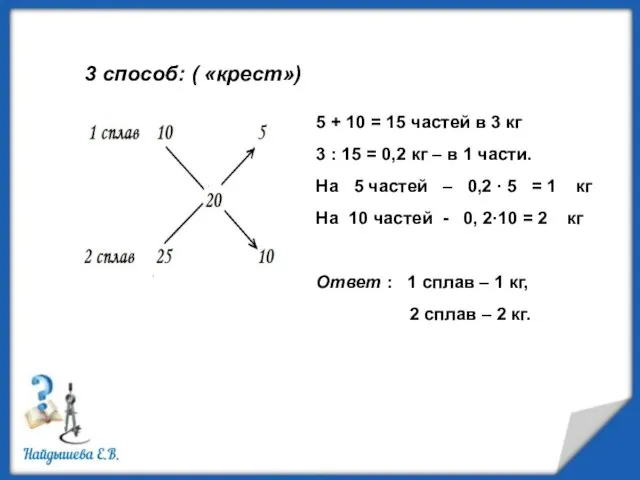
3 способ: ( «крест»)
5 + 10 = 15 частей в 3 кг
3 : 15 = 0,2 кг – в 1 части.
На 5 частей – 0,2 ∙ 5 = 1 кг
На 10 частей - 0, 2∙10 = 2 кг
Ответ : 1 сплав – 1 кг,
2 сплав – 2 кг.