Основы медицинской статистики и организации статистического исследования. Статистический анализ

Доказательная медицина (англ. Evidence-based medicine — медицина, основанная на доказательствах) — подход к медицинской практике, при котором решения о применении профилактических, диагностических и лечебных мероприятий принимаются исходя из имеющихся доказательств их эффективности и безопасности.
Статистика – общественная наука, изучающая количественную сторону массовых общественных явлений в неразрывной связи с их качественными особенностями.
Медицинская статистика – наука, изучающая общественное здоровье и здравоохранение, которая с помощью математических приемов и методов способствует разработке мер по оздоровлению населения.

Разделы медицинской статистики:
- Статистика общественного здоровья;
- Статистика здравоохранения;
- Статистика научных исследований или теоретическая
медицинская статистика.
Предметом статистики являются:
- Изучение общественного здоровья;
- Изучение деятельности учреждений здравоохранения;
- Научно-исследовательская работа;
- Работа над методикой проведения медико-статистических
исследований.

Этапы статистического исследования.
1.Составление программы и плана
2.Статистическое наблюдение
3.Статистическая сводка в таблицы и группировка, первичная счетная обработка данных.
4.Анализ. Выводы. Рекомендации.
Внедрение в практику.

Абсолютная величина
Это количественный показатель, представляющий собой результат измерения количества объектов или величины показателя.

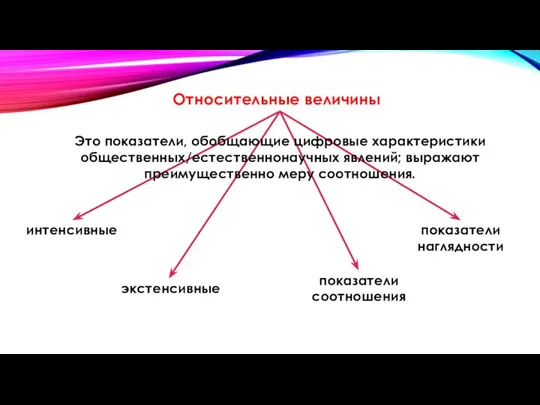
Относительные величины
Это показатели, обобщающие цифровые характеристики общественных/естественнонаучных явлений; выражают преимущественно меру соотношения.
интенсивные
экстенсивные
показатели соотношения
показатели наглядности

1) Интенсивные показатели - показывают частоту явления в среде. В качестве среды обычно выступает некая совокупность объектов (населения, пациентов, случаев), у части которых происходит какое-то явление.
2) Экстенсивные показатели - характеризуют структуру явления, измеряются в процентах. Экстенсивные величины показывают, какую часть составляет отдельная группа единиц в структуре всей совокупности.

3) Показатели соотношения - характеризуют уровень (распространенность) какого-либо явления в среде, непосредственно (биологически) не связанного с данной средой. Данные совокупности могут измеряться в одних величинах, главное условие, что их изменения должны происходить независимо друг от друга. Обычно в таком виде представляются различные индексы, показатели обеспеченности населения.

4) Показатели наглядности – относительные величины, указывающие на соотношение однородных показателей для разных групп или разных периодов.

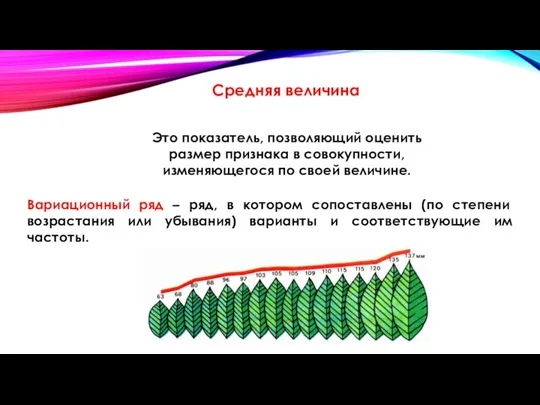
Средняя величина
Это показатель, позволяющий оценить размер признака в совокупности, изменяющегося по своей величине.
Вариационный ряд – ряд, в котором сопоставлены (по степени возрастания или убывания) варианты и соответствующие им частоты.

Варианты (V) – отдельные количественные выражения признака.
Классическое понимание термина "варианта" предполагает, что вариантой называется каждое уникальное значение признака, без учета количества повторов.

Частота (P) – число, показывающее, сколько раз повторяется варианта.
Сумма всех частот (которая равна числу всех исследуемых) обозначается как n.

Показатели вариационных рядов
1) Лимит (Lim) - это критерий, который определяется крайними значениями вариант в вариационном ряду.
Lim = Vmin и Vmax
2) Амплитуда (Am) - это разность крайних вариант.
Am = Vmax — Vmin

3) Мода (Mo) - средняя величина вариационного ряда, соответствующая наиболее часто повторяющейся варианте.
4) Медиана (Me) – значение варианты, делящей вариационный ряд пополам: по обе стороны от нее находится равное число вариант.

5) Средняя арифметическая (M) - это обобщающий показатель, характеризующий размер изучаемого признака.
Средняя арифметическая рассчитывается как отношение суммы значений показателей всех единиц наблюдения к числу всех исследуемых.
Формула для расчета простой средней арифметической:

Формула для расчета взвешенной средней арифметической:

6) Среднее квадратическое отклонение (σ) - мера вариабельности вариационного ряда. Является интегральным показателем, объединяющим все случаи отклонения вариант от средней.
При численности совокупности более 30 единиц, стандартное отклонение рассчитывается по следующей формуле:

Для малых совокупностей - 30 единиц наблюдения и менее - стандартное отклонение рассчитывается по другой формуле:

7) Коэффициент вариации (Сv) - это относительная мера колеблемости вариационного ряда.
Это процентное отношение среднеквадратического отклонения к среднеарифметической величине.
При Сv <10% разнообразие ряда считается слабым,
при Сv от 10 до 20% — средним,
при Сv >20% — сильным.

Динамический ряд – совокупность однородных статистических величин, показывающих изменение какого-либо явления на протяжении определенного промежутка времени.
Уровни ряда – величины, составляющие динамический ряд. Могут быть представлены абсолютными, относительными или средними величинами.