Содержание
- 2. При решении логических задач в олимпиадах по обществознанию не требуется знание специальных логических методов и теорий
- 3. Картезианские правила метода Правило очевидности Правило анализа Правило последовательности Правило полноты
- 4. Критерии решения Задача считается решенной полностью только при наличии правильного ответа и исчерпывающего обоснования Всевозможные схемы,
- 5. Часто встречающиеся ошибки Неправильно проанализирована логическая форма Утверждаемое заключение не следует логически из посылок Пробел в
- 6. 2. Задачи на анализ логической формы
- 7. Задача 1 Директор школы возражает против отмены решения о запрете контроля за прическами Тем самым он
- 8. Решение Свобода причесок (А) Контроль за прическами (не-А) Запрет контроля за прическами (не-не-А) Отмена решения о
- 9. Задача 2 Спикер безапелляционно отверг домыслы о том, что он собирается отменить приказ о запрете уклонения
- 10. Задача 3 В одном классе учились три девушки – Лена, Оля и Катя Лена сказала: «Я
- 11. Решение Лена не самая старшая (1) Оля старше Кати (2) Лена старше Кати (3) Катя -
- 12. Задача 4 Джонс, Смит и Браун подозреваются в преступлении, виновен только один из них Джонс сказал:
- 13. Решение Утверждения Смита и Брауна противоречат друг другу («Это сделал Браун», «Браун не виновен») Значит, один
- 14. 3. Задачи на установление соответствия
- 15. Задача 5 В одном классе учатся Андреев, Борисов и Васильев. Один из них отличник, другой хорошист,
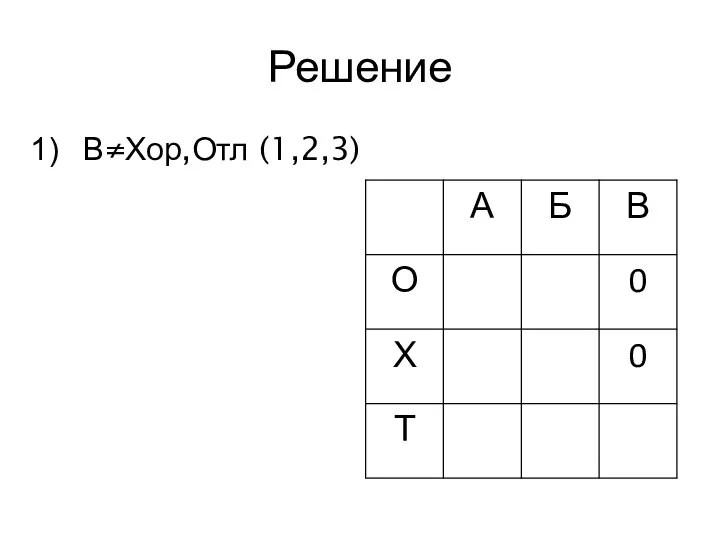
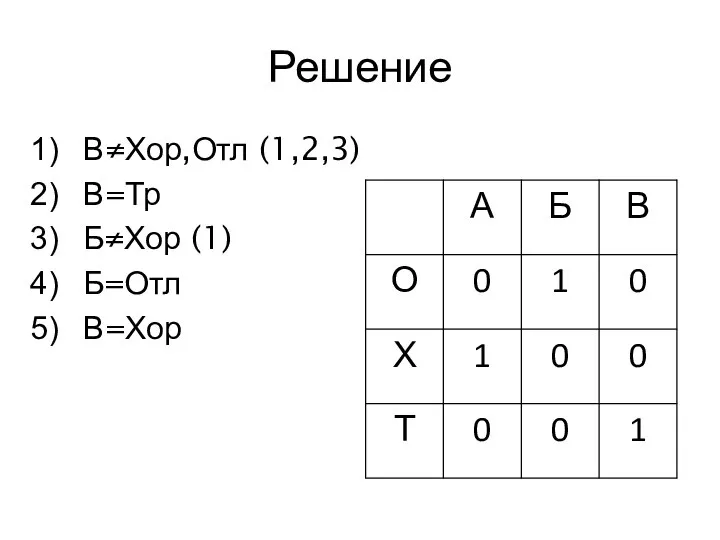
- 16. Решение В≠Хор,Отл (1,2,3)
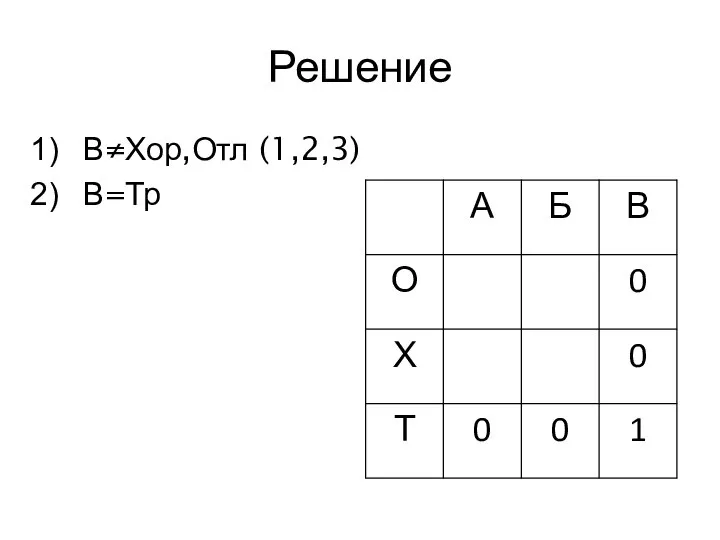
- 17. Решение В≠Хор,Отл (1,2,3) В=Тр
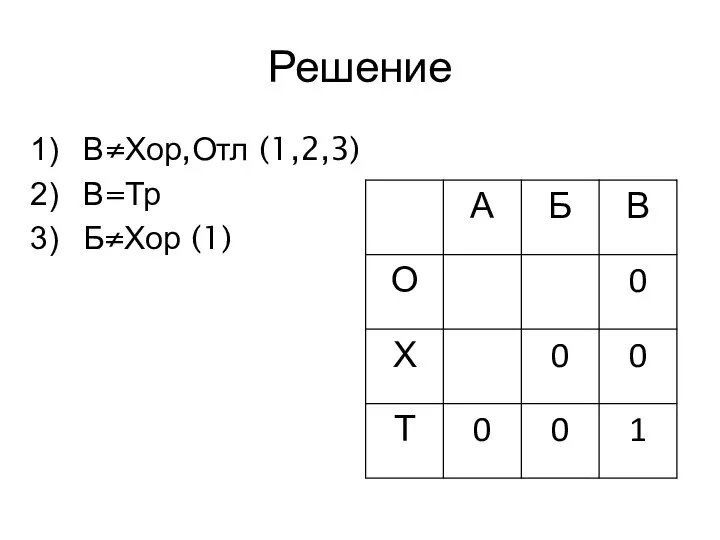
- 18. Решение В≠Хор,Отл (1,2,3) В=Тр Б≠Хор (1)
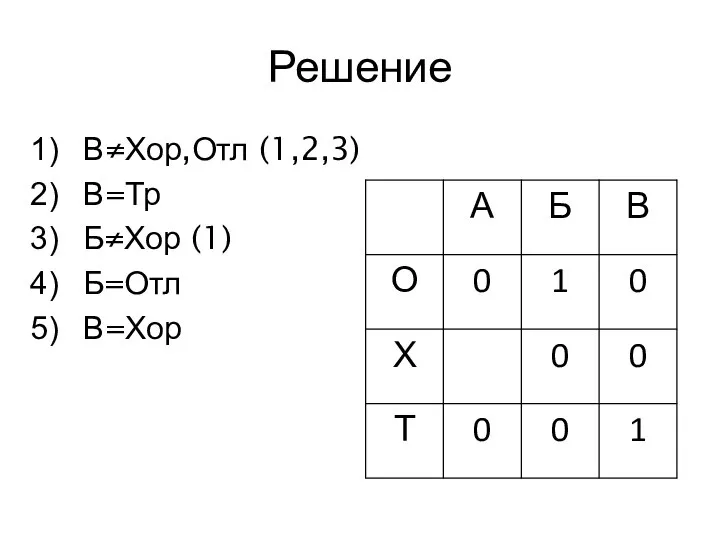
- 19. Решение В≠Хор,Отл (1,2,3) В=Тр Б≠Хор (1) Б=Отл В=Хор
- 20. Решение В≠Хор,Отл (1,2,3) В=Тр Б≠Хор (1) Б=Отл В=Хор
- 21. 4. Задачи с саморекурсивными условиями
- 22. Задача 6 На одном острове живут два племени. Люди племени А всегда говорят правду, а люди
- 23. Решение Что значит ответ «Тарабара?» На вопрос «ты лжец?» любой ответит «Нет» «Тарабара» = «Нет» Значит,
- 24. Задача 7 В одном храме собрались три божества – бог Истины (всегда говорит правду), бог Лжи
- 25. Решение 1 не бог Истины (такой только один, значит, он не может назвать кого-то другого богом
- 26. Задача 8 В семье четверо детей, причем все мальчики в ней (если таковые есть) лгут, а
- 27. Решение Допустим, что первый ребенок – девочка Тогда её высказывание должно быть истинным, но это невозможно,
- 28. Решение Допустим, что второй ребенок – девочка Тогда её высказывание должно быть истинным, т.е. у нее
- 29. Решение Поскольку двое детей уже точно являются мальчиками, высказывание четвертого ребенка «У меня ровно две сестры»
- 30. Решение Уже трое детей гарантированно являются мальчиками, и, следовательно, высказывание третьего ребенка «У меня ровно два
- 31. Задача 9 В конференции по флогистоноведению участвовали 20 человек – химики (всегда говорят правду), алхимики (всегда
- 32. Решение Допустим, что 14 человек сказали правду. Однако это невозможно, ведь они уже составляют большинство от
- 33. Решение Допустим, что 4 сказали правду, т.е. большинство – это химики, которые всегда говорят правду Однако
- 34. Решение Поскольку известно, что на конференции были химики, ничего не остается, кроме как сделать вывод, что
- 35. Решение Допустим, что химик только один, а второй – пиротехник Раз химик всего один, пиротехников –
- 36. Решение Остается вариант с 2-мя химиками Тогда пиротехников 10 (т.е. 2*5) Тогда алхимиков 20-10-2=8 человек Ответ:
- 37. 5. Задачи на установление количественных соотношений
- 38. Задача 10 В научно-исследовательском институте работают 20 ученых: логики, математики и программисты (никаких других специалистов среди
- 39. Решение Число программистов очевидно кратно 10, поскольку «каждый 10-й программист является математиком» Значит, их либо 10,
- 40. Решение Поскольку «каждый 10-й программист является математиком», число программистов, которые являются математиками 10:10 = 1 человек
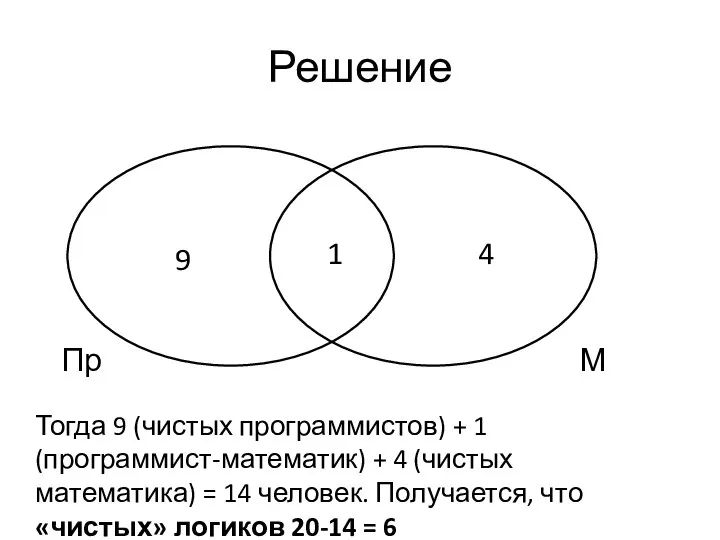
- 41. Решение Пр М 9 1 4 Тогда 9 (чистых программистов) + 1 (программист-математик) + 4 (чистых
- 42. Решение Известно, однако, что не все логики «чистые»: среди логиков треть является программистами и треть –
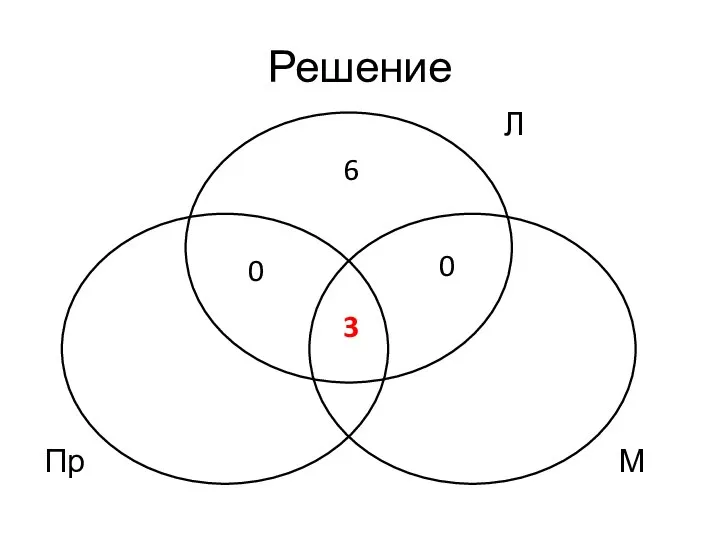
- 43. Решение Допустим, общее число логиков – 9. Треть от 9 равна 3, а значит, 3 логика
- 44. Решение Пр М 6 3 0 Л 0
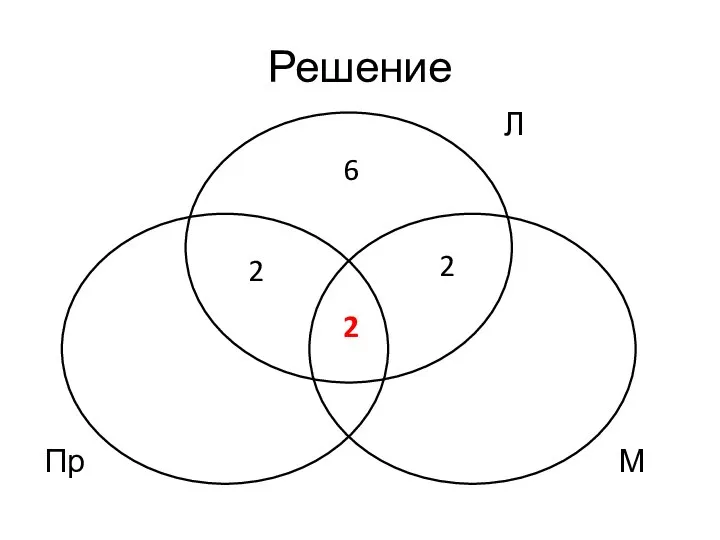
- 45. Решение Допустим, общее число логиков – 12 Треть от 12 равна 4, а значит, 4 логика
- 46. Решение Пр М 6 2 2 Л 2
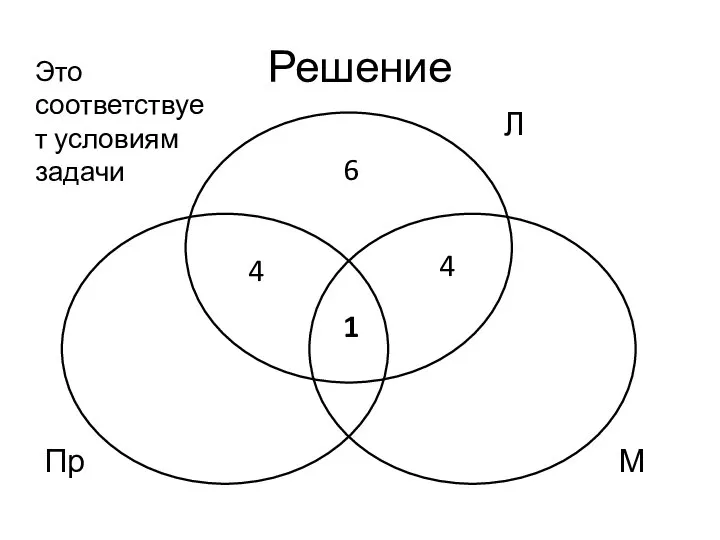
- 47. Решение Допустим, общее число логиков – 15 Треть от 15 равна 5, а значит, 5 логиков
- 48. Решение Пр М 6 1 4 Л 4 Это соответствует условиям задачи
- 49. Решение Проверим последний случай, когда общее число логиков – 18 18:3 = 6 Значит, среди логиков
- 51. Скачать презентацию







































 Портфолио 3В класса
Портфолио 3В класса У кошки в миске
У кошки в миске Звук и буква Ш
Звук и буква Ш Музыкально-дидактическая игра Дятел на развитие чувства ритма у детей старшего дошкольного возраста
Музыкально-дидактическая игра Дятел на развитие чувства ритма у детей старшего дошкольного возраста Традиционная программа подготовки Школа 2100
Традиционная программа подготовки Школа 2100 Нарисуем снегиря
Нарисуем снегиря Чьи это слова? Викторина
Чьи это слова? Викторина Су-Джок терапия в работе по речевому развитию детей 5-8 лет
Су-Джок терапия в работе по речевому развитию детей 5-8 лет Валентинка из салфеток
Валентинка из салфеток Интерактивные технологии контроля результатов обучения. Лекция 8
Интерактивные технологии контроля результатов обучения. Лекция 8 Праздник для маленьких сказочников. Проект
Праздник для маленьких сказочников. Проект Физминутки для глаз. Ёлочка
Физминутки для глаз. Ёлочка Аттестационная работа. Методическая разработка по выполнению проекта Who are you mr. Holmes
Аттестационная работа. Методическая разработка по выполнению проекта Who are you mr. Holmes Как мы быстро подросли, во вторую младшую пошли
Как мы быстро подросли, во вторую младшую пошли Чьи уши (игра)
Чьи уши (игра) Мнемотаблицы заучивание стихотворения Одуванчик
Мнемотаблицы заучивание стихотворения Одуванчик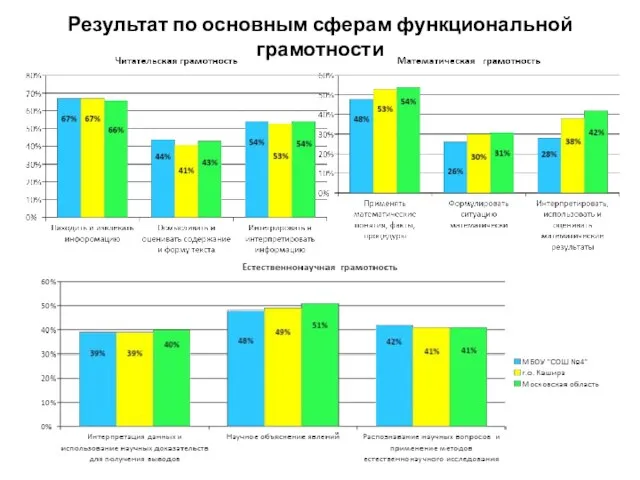 Результат по основным сферам функциональной грамотности
Результат по основным сферам функциональной грамотности Новые педагогические технологии в сфере деятельности дополнительного образования
Новые педагогические технологии в сфере деятельности дополнительного образования Паровозик. Игра с детьми
Паровозик. Игра с детьми Рисуем музыку
Рисуем музыку Рекомендации для родителей по формированию навыков самообслуживания умственно отсталых дошкольников
Рекомендации для родителей по формированию навыков самообслуживания умственно отсталых дошкольников Физкутминутка
Физкутминутка Формирование ключевых компетенций учащихся на уроках химии
Формирование ключевых компетенций учащихся на уроках химии Использование ИКТ в обучении диалогической речи на уроке
Использование ИКТ в обучении диалогической речи на уроке Три ошибки при формировании читательской грамотности, которые Вам никогда не захочется повторять
Три ошибки при формировании читательской грамотности, которые Вам никогда не захочется повторять Осень в Россошанском крае. Конкурс рисунков
Осень в Россошанском крае. Конкурс рисунков Детское объединение Добрые волшебники
Детское объединение Добрые волшебники Разгадайте ребусы
Разгадайте ребусы