ЭВОЛЮЦИЯ СЛОЖНЫХ СИСТЕМ ПО ЗОЛОТОЙ ПРОПОРЦИИ к.ф.-м.н., с.н.с. Харитонов Анатолий Сергеевич Российский государственный социальны
Содержание
- 2. Фундаментальная проблема Известные динамические теории описывают эволюцию замкнутых систем к устойчивому равновесному состоянию, которое может нарушаться
- 3. Фундаментальное противоречие Система, состоящая из одинаковых или тождественных частиц, эволюционирует, после возмущения, к максимальному хаосу. Система,
- 4. Проблема Как в теорию ввести структуру динамических элементов, чтобы за счет ее резонансных взаимодействий можно было
- 5. Новое определение энтропии К - число рассматриваемых микросостояний системы, fi -вероятность i-го микросостояния. Статистическая энтропия равна
- 6. Опыт тройственности числа Число используется в трех смыслах : 1. количество элементов и функций в системе,
- 7. Опытные числовые ряды Натуральный ряд чисел: 1,2,3,4,5, …или Аn=n - справедлив для линейных систем . При
- 8. Рекуррентные ряды Ряд Фибоначчи 0,1,1,2,3,5,8,13,21,34,55,… описывает нелинейные (и биологические) системы. Ряд Люка 2,1,3,4,7,11,18,29,47,… описывает двойственные нелинейные
- 9. Закон рекурсии Аn+2= An+1+An . Для любых начальных значений А1≥0 и A2>0 рекурсия приводит при n→
- 10. Золотая пропорция и статистика Умножение золотой пропорции самой на себя по формуле бинома Ньютона порождает биномиальное
- 11. Пример золотой пропорции Ф=1/ф=1,618…
- 12. Четырехбуквенный код ЗП и геометрия Евклида Это позволяет ввести числа, удовлетворяющие теореме Пифагора
- 13. Фрактальные свойства золотой пропорции Определенное последовательное разбиение единицы на части с помощью золотой пропорции (ЗП) порождает
- 14. Фрактальные свойства чисел 2= (Fn+Ln)/Fn+1 3= (Ln+2 - Fn)/Fn+1 5= (Ln+Ln+2)/Fn+1 7= (Fn +2 Ln+Ln+2)/Fn+1 8=
- 15. К описанию сложных систем Формула полной вероятности позволяет учесть три смысла числа, используемые для описания системы:
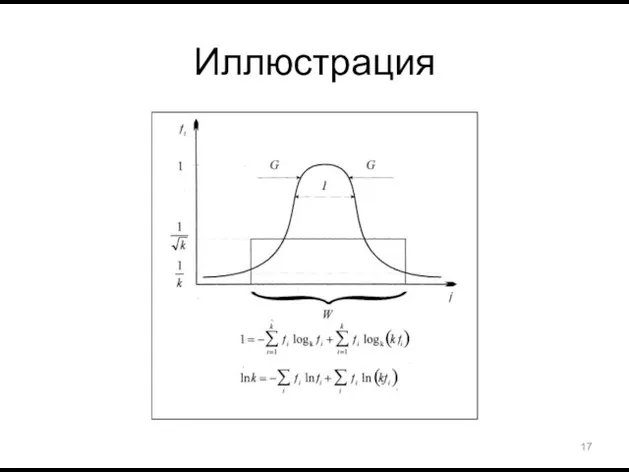
- 16. Целое, меры хаоса и порядка Целое (единицу) можно представить в виде суммы мер хаоса и порядка:
- 17. Иллюстрация
- 18. Симметрия мер хаоса и порядка Постулируем баланс мер хаоса и порядка в трех классах переменных: Н(p,q,l)
- 19. Модель равновесия Баланс мер хаоса и порядка можно толковать как равновесие процессов рассеяния и концентрации энергии
- 20. Специфика описания триединства Трехсущностные функции не удовлетворяют в общем случае условиям существования: производной /К.Вейерштрассе/, температуры /Ф.Фробениус/,
- 21. «Сила» самодвижения Свободная энергия образования сложной системы имеет вид: Fmin= E- Ɵ{S(p)+S(q)+S(l)}max и характеризуется тремя энтропиями,
- 22. Живой организм уходит или стремится к равновесию? Живой организм уходит от термодинамического равновесия. Живой организм стремится
- 23. Фундаментальное отличие живого от косного Живой организм стремится к своему равновесию преимущественно за счет увеличения структурного
- 24. Человек - 1) потребитель, 2) производитель , 3) управленец Развитие общественных отношений приводит к специализации труда
- 25. тройственный баланс как инвариант экономического описания Взаимосвязанные изменения трех энтропий, характеризующих развитие личности, позволяют установить тройственный
- 26. Социальный вывод Стратегическая цель социального управления – тройственная гармонизация отношений – задана законами самодвижения круговорота природы
- 27. Модель развития общества Современные представления о развитии общества по «тройной спирали» взаимодействия государства, бизнеса и науки
- 28. Математическая новизна Описание самодвижения сложных систем возможно при разработке математического аппарата на новой аксиоме разбиения целого
- 30. Скачать презентацию


























 Сказка про "ЖИ" и "ШИ".
Сказка про "ЖИ" и "ШИ".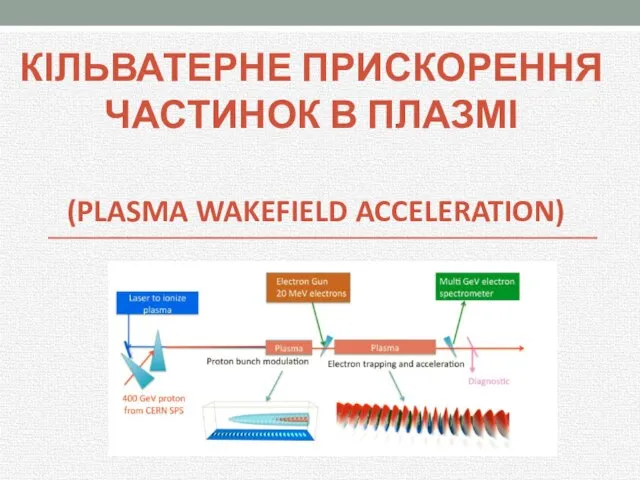 КІЛЬВАТЕРНЕ ПРИСКОРЕННЯ ЧАСТИНОК В ПЛАЗМІ
КІЛЬВАТЕРНЕ ПРИСКОРЕННЯ ЧАСТИНОК В ПЛАЗМІ  ЯДЕРНОЕ ОБРАЗОВАНИЕ В РОССИИ
ЯДЕРНОЕ ОБРАЗОВАНИЕ В РОССИИ Презентация на тему Суд и процесс
Презентация на тему Суд и процесс  Энергия ядра. Взгляд в будущее
Энергия ядра. Взгляд в будущее Плитка керамамараций
Плитка керамамараций сложные разрезы
сложные разрезы Ошибки восприятия в деловом общении
Ошибки восприятия в деловом общении Методы и стратегии управления конфликтными ситуациями Как правильно вести себя в конфликтной ситуации
Методы и стратегии управления конфликтными ситуациями Как правильно вести себя в конфликтной ситуации Презентация к уроку истории в 7классе
Презентация к уроку истории в 7классе Исследовательская работа на тему «история моды»
Исследовательская работа на тему «история моды» Системы управления проектами в режиме онлайн
Системы управления проектами в режиме онлайн Урок развития речи
Урок развития речи Admiral Nelson’s Life
Admiral Nelson’s Life Logistic Management of investment-construction project
Logistic Management of investment-construction project Презентация на тему Государственный строй стран мира
Презентация на тему Государственный строй стран мира Модель проведения муниципального Форума работников системы образования
Модель проведения муниципального Форума работников системы образования Лекарственные растения
Лекарственные растения Исторический костюм
Исторический костюм Сексуальные мотивы в рекламе
Сексуальные мотивы в рекламе Когда на Руси появилось государство?
Когда на Руси появилось государство? Насыщенный и ненасыщенный пар влажность воздуха кипение
Насыщенный и ненасыщенный пар влажность воздуха кипение Сердечные заболевания. Ароматы для улучшения работы сердца. Лекция 25
Сердечные заболевания. Ароматы для улучшения работы сердца. Лекция 25 Подробности Write. Процедура вывода WriteLn. Курсор
Подробности Write. Процедура вывода WriteLn. Курсор КИСЛОРОД
КИСЛОРОД УПРАВЛЕНИЕ ВОСПИТАТЕЛЬНОЙ РАБОТЫ И МОЛОДЕЖНОЙ ПОЛИТИКИ ВГАСУ
УПРАВЛЕНИЕ ВОСПИТАТЕЛЬНОЙ РАБОТЫ И МОЛОДЕЖНОЙ ПОЛИТИКИ ВГАСУ Климат и природные зоны Земли
Климат и природные зоны Земли  Как проводился эксперимент и каковы результаты?
Как проводился эксперимент и каковы результаты?