Проскальзывание фазы, поглощение электромагнитного излучения и формирование отклика в детекторах на основе узких полосок сверхп
Содержание
- 2. Структура диссертации Гл. 1 - обзорная Гл. 2. Теоретический анализ работы сверхпроводникового детектора на кинетической индуктивности
- 3. Глава 2 Теоретический анализ работы сверхпроводникового детектора на кинетической индуктивности Поглощение электромагнитного излучения и формирование индуктивного
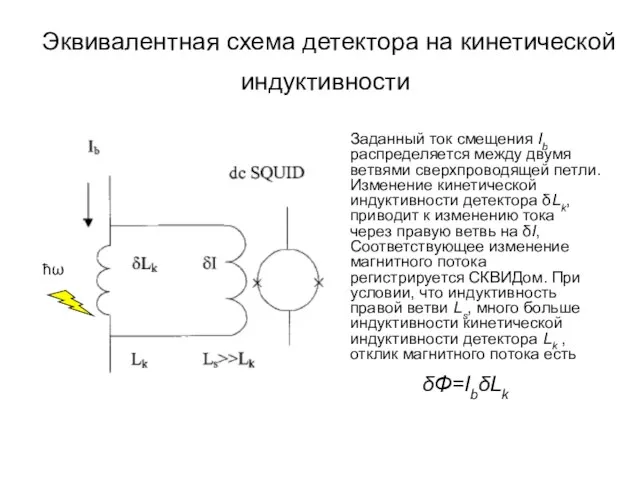
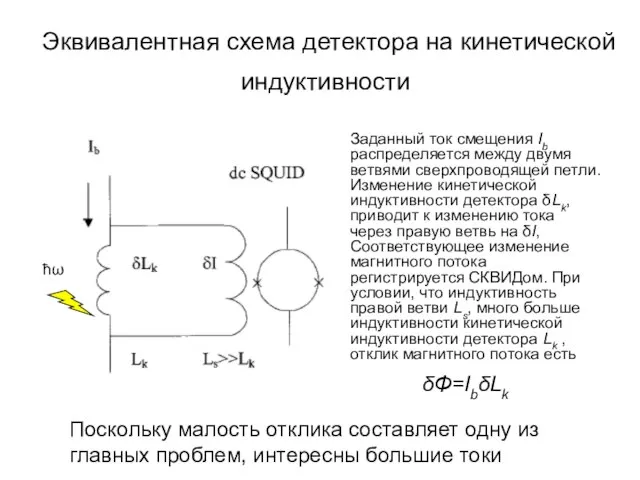
- 4. Эквивалентная схема детектора на кинетической индуктивности Заданный ток смещения Ib распределяется между двумя ветвями сверхпроводящей петли.
- 5. Эквивалентная схема детектора на кинетической индуктивности Заданный ток смещения Ib распределяется между двумя ветвями сверхпроводящей петли.
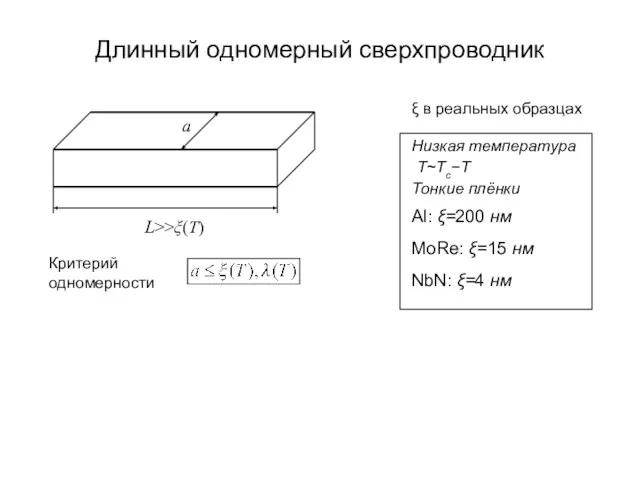
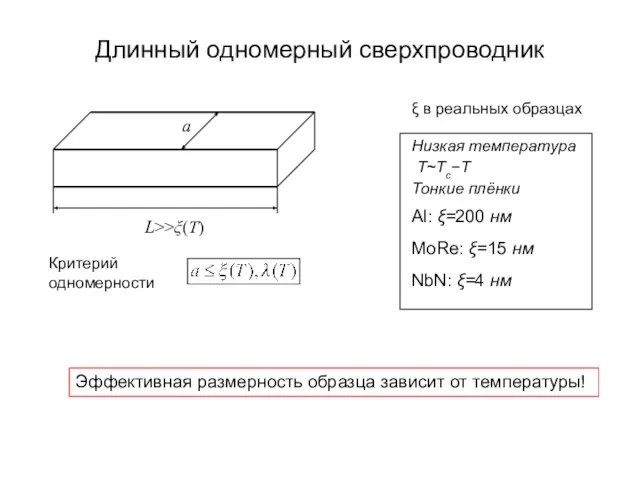
- 6. Длинный одномерный сверхпроводник a L>>ξ(T) Низкая температура Т~Tc−T Al: ξ=200 нм NbN: ξ=4 нм MoRe: ξ=15
- 7. Поглощение в сверхпроводнике в бестоковом случае Отклик кинетической индуктивности при низкой температуре в бестоковом случае
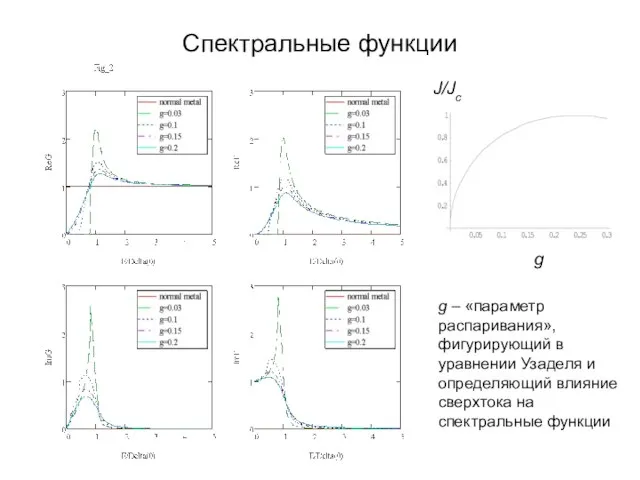
- 8. Спектральные функции g – «параметр распаривания», фигурирующий в уравнении Узаделя и определяющий влияние сверхтока на спектральные
- 9. Исходные уравнения Состояние грязного сверхпроводника в методе Узаделя описывается матричной квзиклассической функцией Грина . . Компоненты
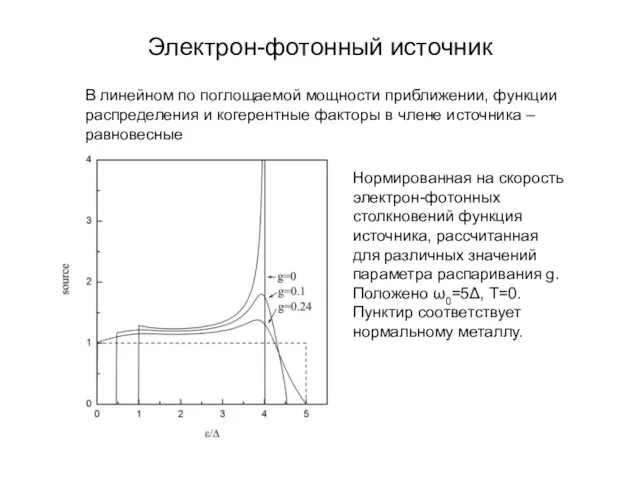
- 10. Электрон-фотонный источник Член источника получается из келдышевой части уравнения Узаделя Монохроматический сигнал f – функция распределения
- 11. Электрон-фотонный источник В линейном по поглощаемой мощности приближении, функции распределения и когерентные факторы в члене источника
- 12. Вычисление когерентных факторов Запаздывающее уравнение Узаделя Уравнение самосогласования Ф - параметризация
- 13. Линеаризованные кинетические уравнения Линейное приближение: , , , - равновесные функции распределения квазичастиц и фононов, Линеаризованное
- 14. Линеаризованное кинетическое уравнение для фононов где - скорость поглощения фононов с порождением квазичастиц, - скорость ухода
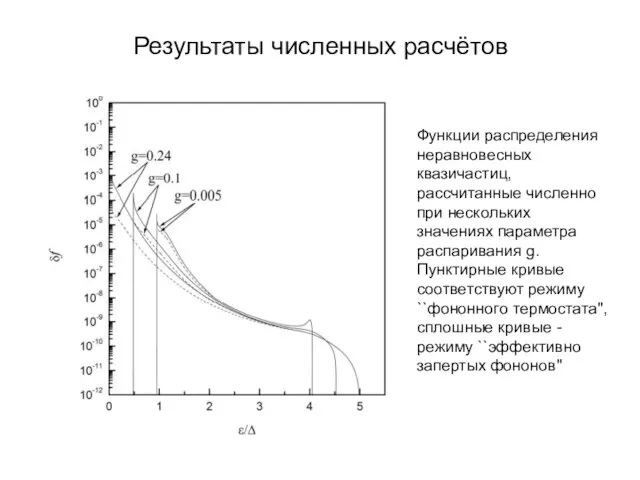
- 15. Результаты численных расчётов Функции распределения неравновесных квазичастиц, рассчитанные численно при нескольких значениях параметра распаривания g. Пунктирные
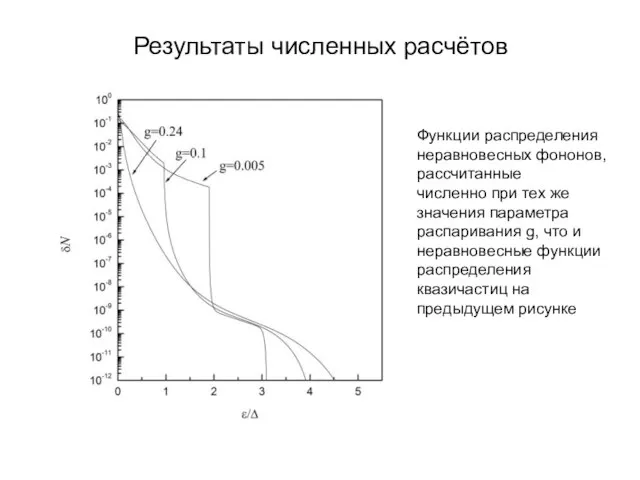
- 16. Результаты численных расчётов Функции распределения неравновесных фононов, рассчитанные численно при тех же значения параметра распаривания g,
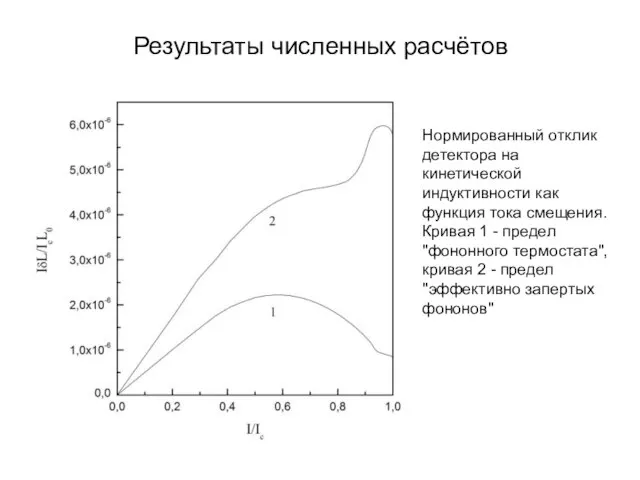
- 17. Результаты численных расчётов Нормированный отклик детектора на кинетической индуктивности как функция тока смещения. Кривая 1 -
- 18. Глава 3 Проскальзывание фазы в диффузной сверхпроводящей нанопроволоке Микроскопическое рассмотрение задачи о флуктуационном проскальзывании фазы параметра
- 19. Длинный одномерный сверхпроводник a L>>ξ(T) Низкая температура Т~Tc−T Al: ξ=200 нм Эффективная размерность образца зависит от
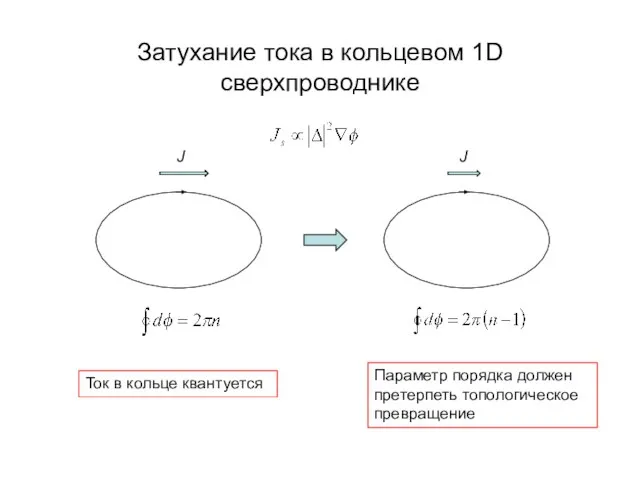
- 20. Затухание тока в кольцевом 1D сверхпроводнике J Ток в кольце квантуется
- 21. Затухание тока в кольцевом 1D сверхпроводнике J J Ток в кольце квантуется Параметр порядка должен претерпеть
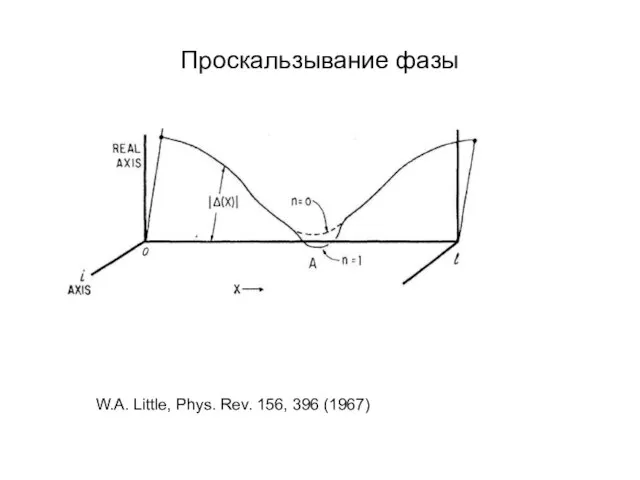
- 22. Проскальзывание фазы W.A. Little, Phys. Rev. 156, 396 (1967)
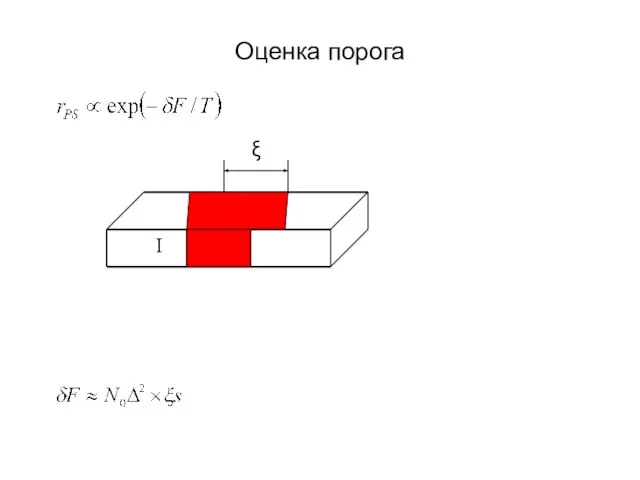
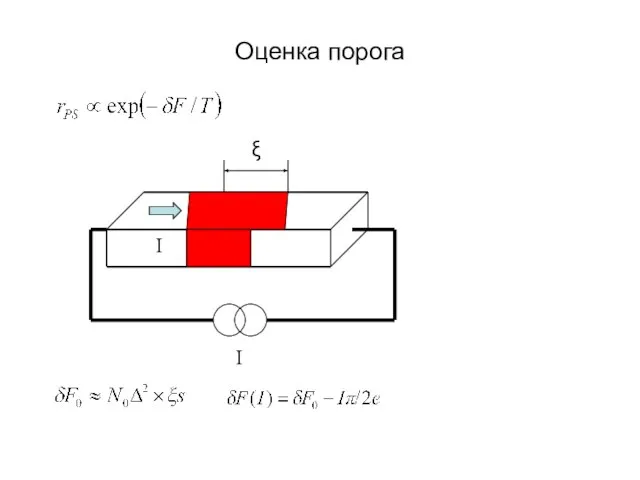
- 23. Оценка порога I ξ
- 24. Оценка порога I I ξ
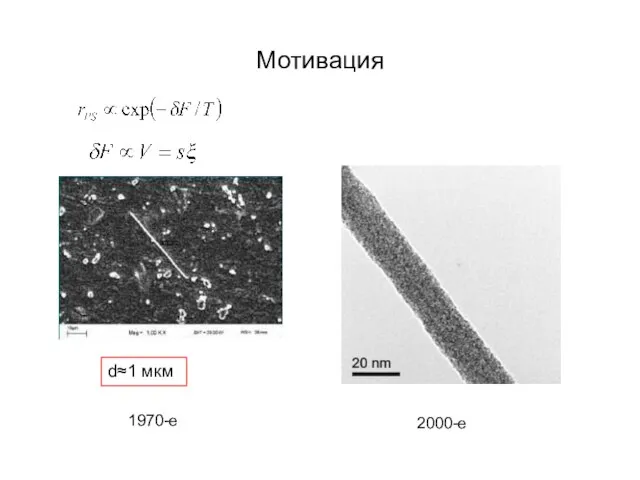
- 25. Мотивация 2000-e 1970-e d≈1 мкм
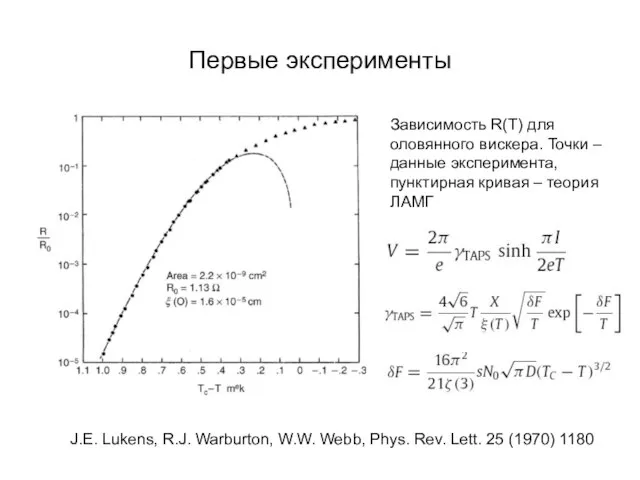
- 26. Первые эксперименты J.E. Lukens, R.J. Warburton, W.W. Webb, Phys. Rev. Lett. 25 (1970) 1180 Зависимость R(T)
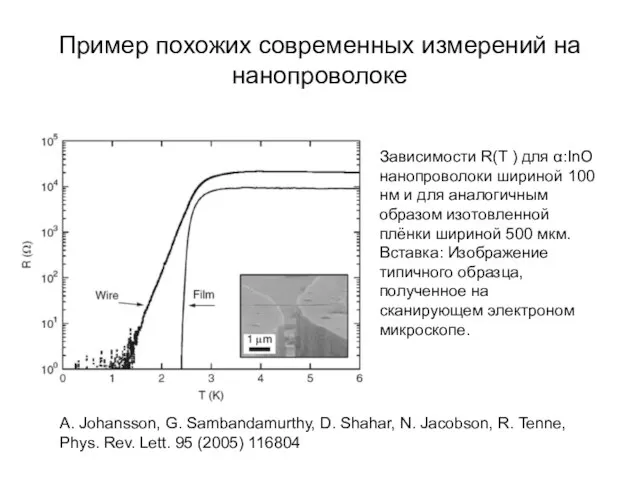
- 27. Пример похожих современных измерений на нанопроволоке Зависимости R(T ) для α:InO нанопроволоки шириной 100 нм и
- 28. Теоретические работы последних 15 лет, посвящённые флуктуационному проскальзыванию фазы D.S. Golubev, A.D. Zaikin, Phys. Rev. B
- 29. Однако, до настоящего времени не было проведено расчетов зависимости барьера свободной энергии от тока и магнитного
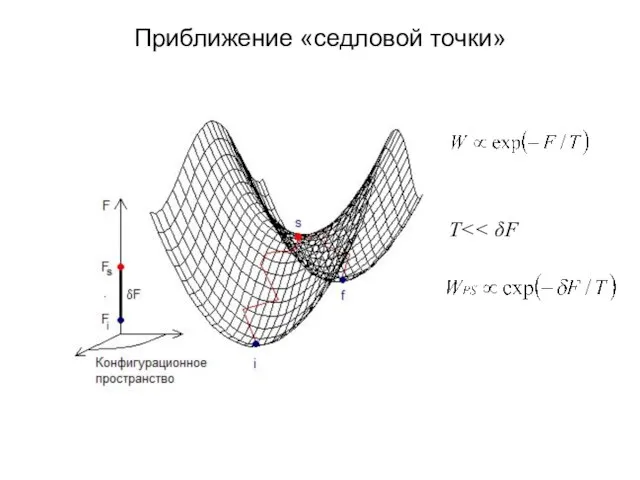
- 30. Приближение «седловой точки» T
- 31. Решение Ланжера-Амбегаокара , J.S. Langer and V. Amegaokar, Phys. Rev. 164, 498 (1967) 1-е уравнение ГЛ
- 32. Результаты Ланжера-Амбегаокара (в пределе нулевого тока) J.S. Langer and V. Amegaokar, Phys. Rev. 164, 498 (1967)
- 33. Уравнение Узаделя для проскальзывания фазы G и F – мацубаровские функции Грина; G2+|F|2=1 Δ – координатно-зависимый
- 34. Вычисление порога свободной энергии . Узаделевское выражение для свободной энегргии
- 35. Вычисление порога свободной энергии . Узаделевское выражение для свободной энергии
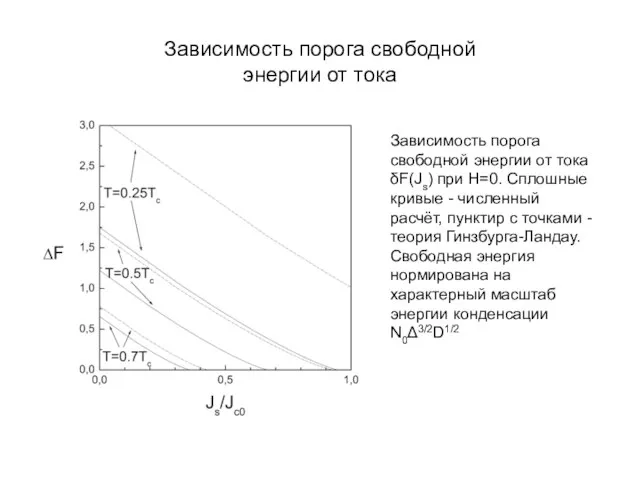
- 36. Зависимость порога свободной энергии от тока Зависимость порога свободной энергии от тока δF(Js) при H=0. Сплошные
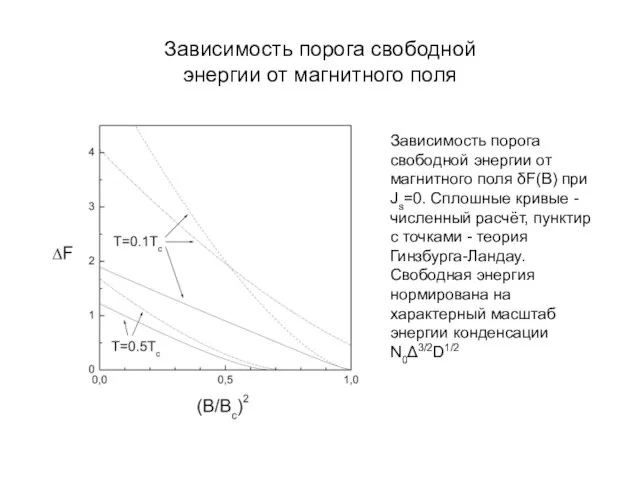
- 37. Зависимость порога свободной энергии от магнитного поля Зависимость порога свободной энергии от магнитного поля δF(B) при
- 38. Аналитическое решение вблизи критического поля При Г→Гс удаётся свести уравнение Узаделя к замкнутому уравнению для параметра
- 39. Аналитическое решение вблизи критического поля , Решение для «седловой точки» . , Порог свободной энергии
- 40. Глава 4 Моделирование формы отклика SSPD Оптимизация сверхпроводникового однофотонного детектора (SSPD) Исследование возможности применения SSPD, разрешающего
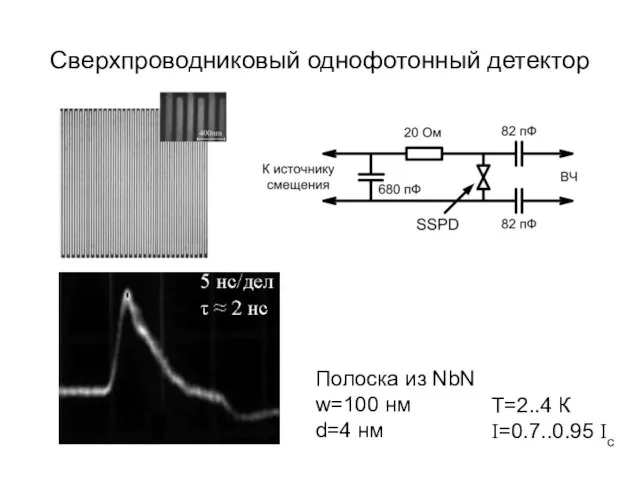
- 41. Сверхпроводниковый однофотонный детектор Полоска из NbN w=100 нм d=4 нм T=2..4 К I=0.7..0.95 Ic
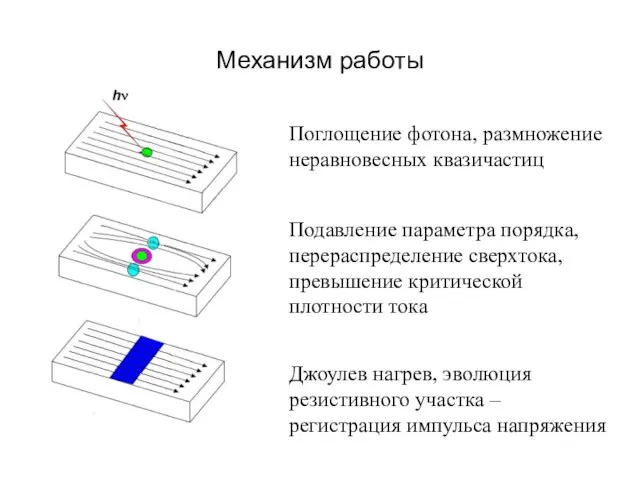
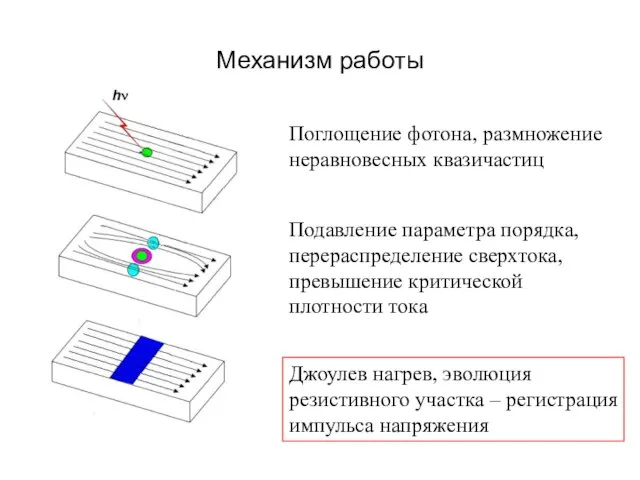
- 42. Механизм работы Поглощение фотона, размножение неравновесных квазичастиц Подавление параметра порядка, перераспределение сверхтока, превышение критической плотности тока
- 43. Механизм работы Поглощение фотона, размножение неравновесных квазичастиц Подавление параметра порядка, перераспределение сверхтока, превышение критической плотности тока
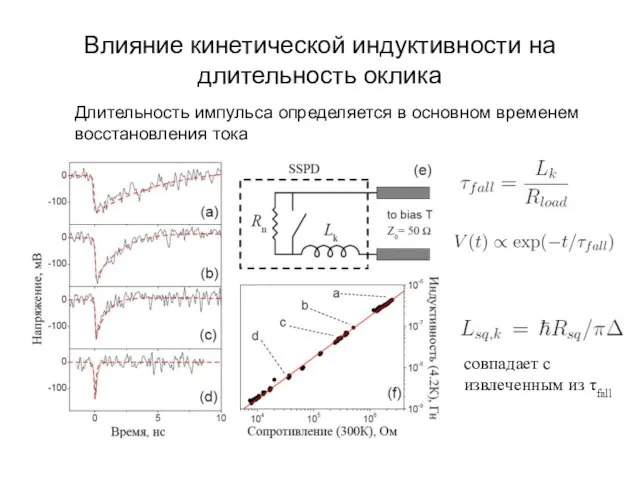
- 44. Влияние кинетической индуктивности на длительность оклика Длительность импульса определяется в основном временем восстановления тока совпадает с
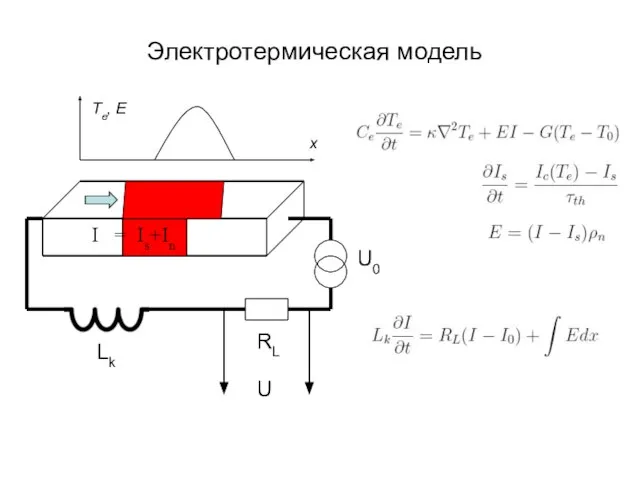
- 45. Электротермическая модель U0 RL Lk U I = Is+In Te, E x
- 46. Константы Температура термостата Т0=4.2 К Критическая температура Тс=10 К Эффективная длина когерентности ξ=7.5 нм Постоянная Зоммерфельда
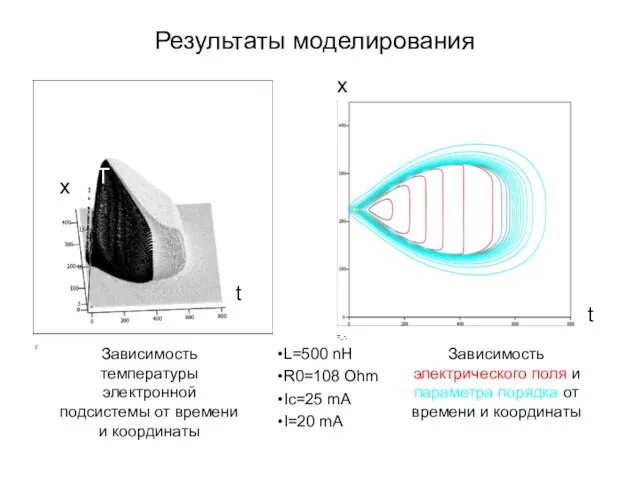
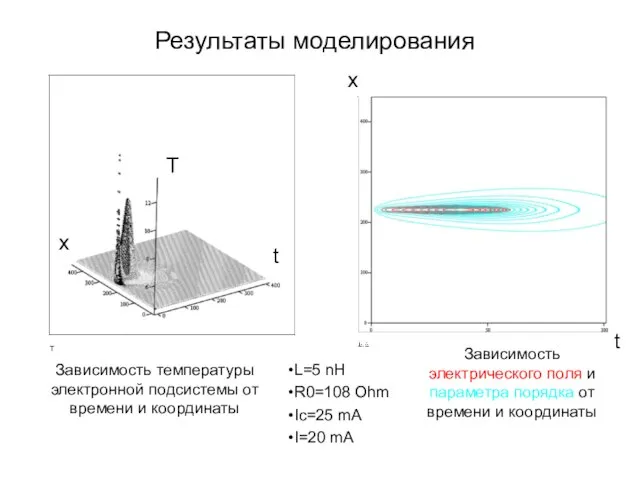
- 47. Зависимость температуры электронной подсистемы от времени и координаты L=500 nH R0=108 Ohm Ic=25 mA I=20 mA
- 48. Зависимость температуры электронной подсистемы от времени и координаты Зависимость электрического поля и параметра порядка от времени
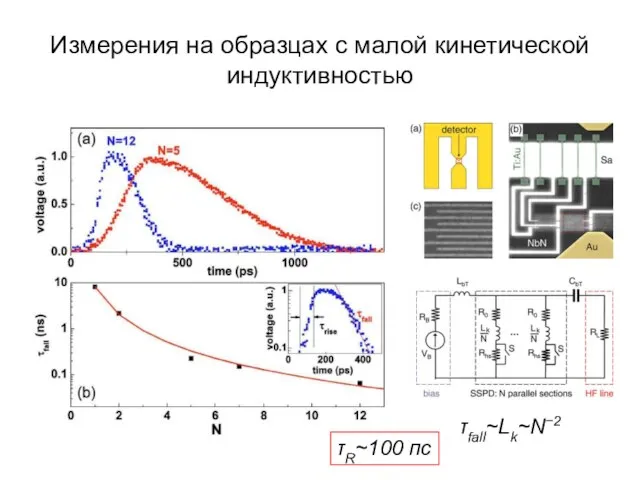
- 49. Измерения на образцах с малой кинетической индуктивностью τfall~Lk~N−2 τR~100 пс
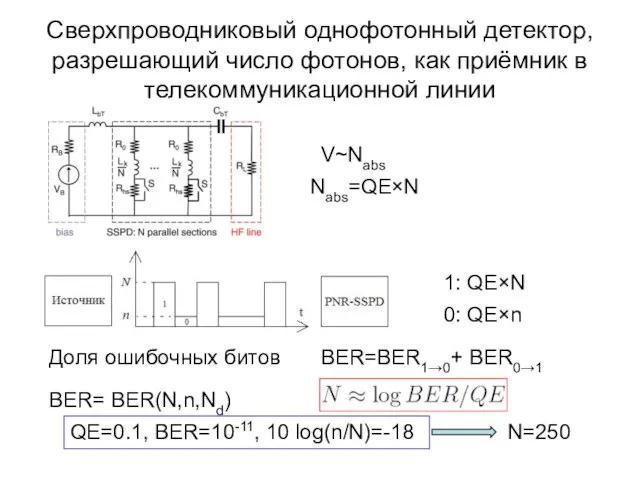
- 50. Сверхпроводниковый однофотонный детектор, разрешающий число фотонов, как приёмник в телекоммуникационной линии Доля ошибочных битов Nabs=QE×N V~Nabs
- 51. Положения, выносимые на защиту по результатам гл.2 Поглощение энергии высокочастотного электромагнитного поля в диффузном сверхпроводнике может
- 52. Положения, выносимые на защиту по результатам гл.3 Зависимости порога свободной энергии для процесса проскальзывания фазы в
- 53. Положения, выносимые на защиту по результатам гл.4 Уменьшение кинетической индуктивности сверхпроводникового однофотонного детектора до величин менее
- 54. Спасибо за внимание!
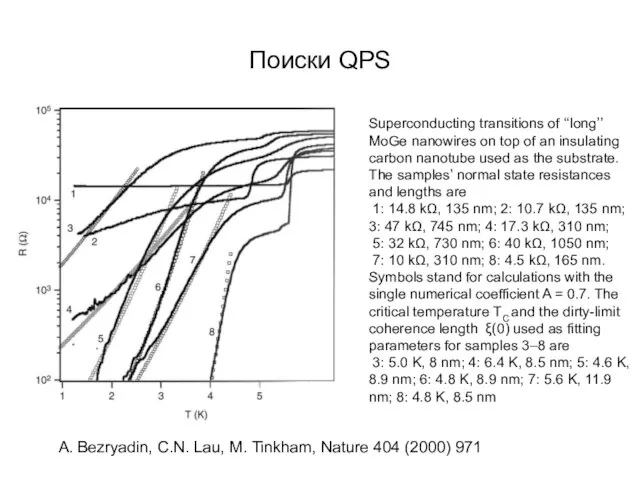
- 56. Поиски QPS Superconducting transitions of ‘‘long’’ MoGe nanowires on top of an insulating carbon nanotube used
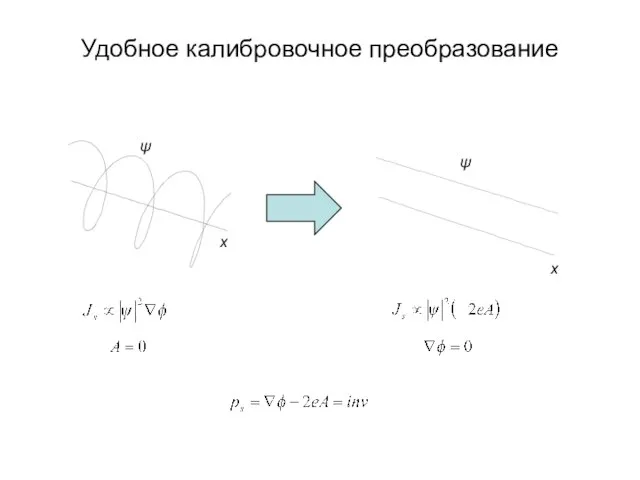
- 57. Удобное калибровочное преобразование ψ x
- 58. Удобное калибровочное преобразование ψ ψ x x
- 60. Скачать презентацию



























 Бессмертная комедия А. С. Грибоедова «Горе от ума»
Бессмертная комедия А. С. Грибоедова «Горе от ума» Урок коллективного посещения в 5 классе
Урок коллективного посещения в 5 классе ПЕДАГОГИЧЕСКИЙ СОВЕТОДАРЁННЫЕ ДЕТИ: реалии, проблемы, перспективы.
ПЕДАГОГИЧЕСКИЙ СОВЕТОДАРЁННЫЕ ДЕТИ: реалии, проблемы, перспективы. Ранения. Первая медицинская помощь
Ранения. Первая медицинская помощь Совершенствование сервисно-транспортной инфраструктуры придомовых территорий
Совершенствование сервисно-транспортной инфраструктуры придомовых территорий СТЕКЛЯННЫЕ ТОВАРЫ
СТЕКЛЯННЫЕ ТОВАРЫ Применение электролиза. Основная химическая промышленность
Применение электролиза. Основная химическая промышленность Маршрут прогулки по городу Борисоглебск
Маршрут прогулки по городу Борисоглебск Региональный студенческий хакатон ООО АИС город
Региональный студенческий хакатон ООО АИС город Берегите зрение
Берегите зрение Конкурентные преимущества и перспективы развития казахстанского фондового рынка
Конкурентные преимущества и перспективы развития казахстанского фондового рынка Древние восточные церкви. Православие за рубежом в xх – xxi вв
Древние восточные церкви. Православие за рубежом в xх – xxi вв Pro-психологов: психологическая служба образовательной организации
Pro-психологов: психологическая служба образовательной организации ST Main Page
ST Main Page Лекарственная аллергия
Лекарственная аллергия Знаковые модели. Моделирование и формализация
Знаковые модели. Моделирование и формализация Развитие координационных способностей у юных борцов вольного стиля
Развитие координационных способностей у юных борцов вольного стиля Диплом партнёра центра спортивного комплексного обучения по хоккею г. Сморгони
Диплом партнёра центра спортивного комплексного обучения по хоккею г. Сморгони МЕТОДИКА ПРОВЕДЕНИЯ КОРРЕКЦИОННЫХ ЗАНЯТИЙ
МЕТОДИКА ПРОВЕДЕНИЯ КОРРЕКЦИОННЫХ ЗАНЯТИЙ Политический конфликт
Политический конфликт Чемпионат и первенство города Ярославля по зимнему триатлону
Чемпионат и первенство города Ярославля по зимнему триатлону AI автомобиля в изменчивом мире на примере Ex Machina
AI автомобиля в изменчивом мире на примере Ex Machina Восприятие речи
Восприятие речи Конаково
Конаково Сударыня - Масленица
Сударыня - Масленица Візуальний контакт під час ділової комунікації
Візуальний контакт під час ділової комунікації Технологии проведения избирательной кампании
Технологии проведения избирательной кампании Общественная организацияг.Балаково Саратовской области«Попечительский совет средней школы №11»
Общественная организацияг.Балаково Саратовской области«Попечительский совет средней школы №11»