Содержание
- 2. При жестком возникновении хаоса бифуркация периодического режима приводит к резкой качественной перестройке структуры фазового пространства, включая
- 3. Пусть при μ μкр фазовые траектории из локальной окрестности исчезнувшего аттрактора С должны попадать на какой-то
- 4. Перемежаемость, связанная с касательной (седло-узловой) бифуркацией циклов, наиболее типична для широкого класса ДС. Она была обнаружена
- 5. Например, для отображения на рисунке для возврата изображающей точки служит ветвь графика функции последования на отрезке
- 6. Переход к хаосу через разрушение замкнутой инвариантной кривой Данный бифуркационный механизм возникновения хаотического поведения наблюдается в
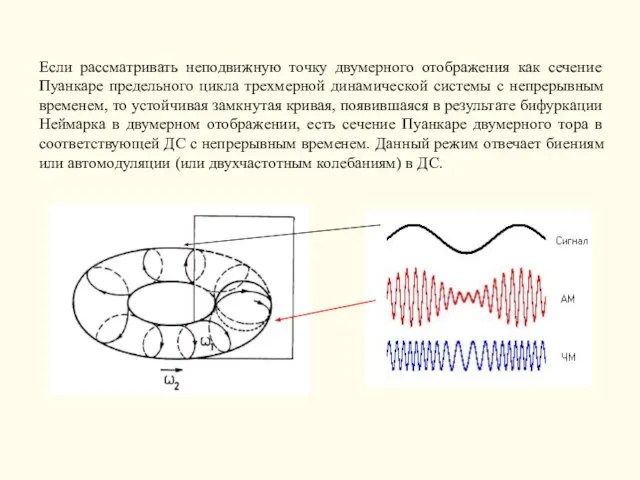
- 7. Если рассматривать неподвижную точку двумерного отображения как сечение Пуанкаре предельного цикла трехмерной динамической системы с непрерывным
- 8. где управляющие параметры определены в интервале 2.0 На рисунке показано преобразование этим отображением области начальных значений,
- 9. Отображение (62) имеет три неподвижные точки: (0, 0), (-1- а, 0) и (1/b, 1- 1/b –
- 11. Скачать презентацию
Слайд 2При жестком возникновении хаоса бифуркация периодического режима приводит к резкой качественной перестройке
При жестком возникновении хаоса бифуркация периодического режима приводит к резкой качественной перестройке

1) касательная (седло-узловая) бифуркация;
2) субкритическая бифуркация удвоения периода (существовавший в системе до бифуркации неустойчивый цикл периода 2 «схлопывается» в устойчивую неподвижную точку; после бифуркации неподвижная точка становится неустойчивой);
3) субкритическая бифуркация Андронова-Хопфа (до бифуркации в системе сосуществуют устойчивая неподвижная точка и неустойчивая замкнутая траектория; в точке бифуркации эта кривая стягивается к неподвижной точке, в результате чего последняя становится неустойчивой).
В случае касательной бифуркации устойчивое состояние равновесие сливается в седловым и исчезает. В двух других случаях неподвижная точка продолжает существовать и после бифуркации, но становится неустойчивой (седловой).
Слайд 3Пусть при μ < μкр система имеет аттрактор С – цикл периода
Пусть при μ < μкр система имеет аттрактор С – цикл периода

Каковы же условия, при которых кризис m-цикла приводит к возникновению перемежающегося хаоса?
Это происходит в том случае, когда в бифуркационной точке μ = μкр уже существует хаотическое множество, которое при μ > μкр становится притягивающим и включает в себя локальную окрестность цикла C так, что фазовая траектория на хаотическом аттракторе время от времени в эту окрестность возвращается.
Слайд 4Перемежаемость, связанная с касательной (седло-узловой) бифуркацией циклов, наиболее типична для широкого класса
Перемежаемость, связанная с касательной (седло-узловой) бифуркацией циклов, наиболее типична для широкого класса

Параметр ε соответствует параметру надкритичности μ – μкр системы, так как в отображении (61) касательная бифуркация имеет место при ε = 0; р – целое число, определяющее порядок экстремума функции последования. Возврат изображающей точки в ограниченный интервал значений x может быть осуществлен различными способами.
(61)
Слайд 5Например, для отображения на рисунке для возврата изображающей точки служит ветвь графика
Например, для отображения на рисунке для возврата изображающей точки служит ветвь графика

В точке бифуркации
Сразу после бифуркации
Слайд 6Переход к хаосу через разрушение замкнутой
инвариантной кривой
Данный бифуркационный механизм возникновения хаотического
Переход к хаосу через разрушение замкнутой
инвариантной кривой
Данный бифуркационный механизм возникновения хаотического

Слайд 7Если рассматривать неподвижную точку двумерного отображения как сечение Пуанкаре предельного цикла трехмерной
Если рассматривать неподвижную точку двумерного отображения как сечение Пуанкаре предельного цикла трехмерной
Слайд 8где управляющие параметры определены в интервале 2.0 < a, b ≤ 4.0.
где управляющие параметры определены в интервале 2.0 < a, b ≤ 4.0.
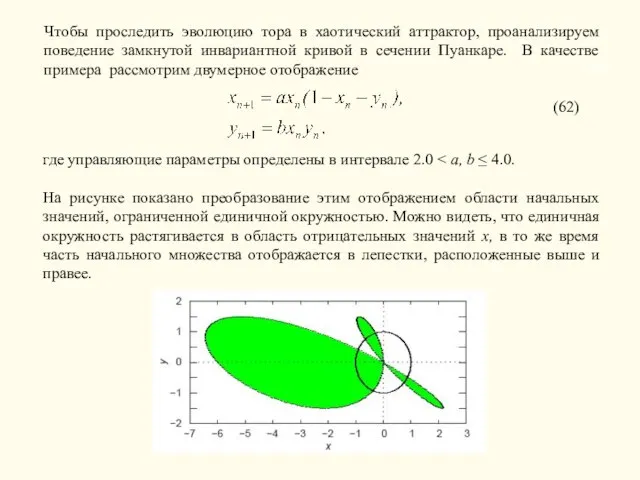
На рисунке показано преобразование этим отображением области начальных значений, ограниченной единичной окружностью. Можно видеть, что единичная окружность растягивается в область отрицательных значений x, в то же время часть начального множества отображается в лепестки, расположенные выше и правее.
(69)
Чтобы проследить эволюцию тора в хаотический аттрактор, проанализируем поведение замкнутой инвариантной кривой в сечении Пуанкаре. В качестве примера рассмотрим двумерное отображение
(62)
Слайд 9Отображение (62) имеет три неподвижные точки:
(0, 0), (-1- а, 0) и
Отображение (62) имеет три неподвижные точки:
(0, 0), (-1- а, 0) и

Анализ на устойчивость дает
Соотношение (63) позволяет определить кривую на плоскости параметров (a, b), при достижении которой (в сторону увеличения параметра a или b) состояние равновесия теряет устойчивость через бифуркацию Неймарка.
В предположении | ρ±| = 1, из (63) следует условие b = 2a /(a – 1), причем выражение под корнем в (63) при этом отрицательно. Таким образом, на линии плоскости параметров b = 2a /(a – 1) рождается замкнутая инвариантная кривая.
(63)
 Рейтинг популярности услуг аутсорсинга среди иностранных компаний, представленных в России Совместный проект аутсорсингового п
Рейтинг популярности услуг аутсорсинга среди иностранных компаний, представленных в России Совместный проект аутсорсингового п Разработка стратегии развертывания приложений
Разработка стратегии развертывания приложений Собственная и примесная проводимость полупроводников
Собственная и примесная проводимость полупроводников  Презентация на тему Развитие жизни в палеозойской эре Ранний палеозой (кембрий, ордовик, силур)
Презентация на тему Развитие жизни в палеозойской эре Ранний палеозой (кембрий, ордовик, силур)  Расчеты по уравнениям реакций, протекающих в растворах
Расчеты по уравнениям реакций, протекающих в растворах Презентация на тему Моя снежинка не растает
Презентация на тему Моя снежинка не растает Календарь-трансформер
Календарь-трансформер Становись партнером и зарабатывай с продажи билетов
Становись партнером и зарабатывай с продажи билетов Типовые приемы в консультировании
Типовые приемы в консультировании Презентация на тему Одежда Средних веков (5 класс)
Презентация на тему Одежда Средних веков (5 класс) Презентация на тему Военные года 1941-1945
Презентация на тему Военные года 1941-1945  Принципы осуществления радиосвязи
Принципы осуществления радиосвязи ООО Алми. Строительная компания
ООО Алми. Строительная компания Алиаскарова Ж.А. Человек науки
Алиаскарова Ж.А. Человек науки Стили речи. Введение в стилистику
Стили речи. Введение в стилистику Исследование и разработка направленного ответвителя с улучшенными характеристиками
Исследование и разработка направленного ответвителя с улучшенными характеристиками Auto Lux. Расширяем возможности микс системы. Набор специальных пигментов от кампании Примо Колор
Auto Lux. Расширяем возможности микс системы. Набор специальных пигментов от кампании Примо Колор СБЕРБАНК ЛИЗИНГ НОВЫЕ ВОЗМОЖНОСТИСЕГОДНЯ
СБЕРБАНК ЛИЗИНГ НОВЫЕ ВОЗМОЖНОСТИСЕГОДНЯ Призер муниципального этапа всероссийской олимпиады школьников по физической культуре Бушковский Никита
Призер муниципального этапа всероссийской олимпиады школьников по физической культуре Бушковский Никита Уважаемые коллеги! От имени коллектива НП Национальная страховая гильдия » примите искренние поздравления с профессиональным
Уважаемые коллеги! От имени коллектива НП Национальная страховая гильдия » примите искренние поздравления с профессиональным  Конспект занятия по развитию речив подготовительной группе детского сада на тему: «Музей почтовых принадлежностей» (с использов
Конспект занятия по развитию речив подготовительной группе детского сада на тему: «Музей почтовых принадлежностей» (с использов Функции русского языка в современном мире
Функции русского языка в современном мире Семейный очаг
Семейный очаг Александр Александрович Блок
Александр Александрович Блок О внедрении системы электронного общения с родителями 10 а класса МОУ СОШ №17 классного руководителя Печкуровой Е.А
О внедрении системы электронного общения с родителями 10 а класса МОУ СОШ №17 классного руководителя Печкуровой Е.А Мотивация и стимулирование труда персонала в государственном учреждении КГБОУ Барнаульская общеобразовательная школа-интернат №3
Мотивация и стимулирование труда персонала в государственном учреждении КГБОУ Барнаульская общеобразовательная школа-интернат №3 Проектирование технологического процесса на изготовление детали чашка каретки левая с годовой программой выпуска 40000 штук
Проектирование технологического процесса на изготовление детали чашка каретки левая с годовой программой выпуска 40000 штук Портреты великих исполнителей
Портреты великих исполнителей