10 способов решения квадратного уравнения

Цели курса:
Знакомство с новыми методами решения квадратных уравнений
Углубление знаний по теме «Квадратные уравнения»
Развитие математических, интеллектуальных способностей, навыков исследовательской работы
Создание условий для самореализации личности

Задачи курса:
Познакомить учащихся с новыми способами решения квадратных уравнений
Закрепить умения решать уравнения известными способами
Ввести теоремы, позволяющие решать уравнения нестандартными способами
Продолжить формирование общеучебных навыков, математической культуры
Содействовать формированию интереса к исследовательской деятельности
Создать условия для учащихся в реализации и развитии интереса к предмету математика
Подготовить учащихся к правильному выбору профильного направления

Содержание программы
Тема 1. Введение. 1 час.
Определение кв.уравнения. Полные и неполные кв. уравнения. Методы их решения. Анкетирование.
Тема 2. Решение кв. уравнений.
Метод разложения на множители
Метод выделения полного квадрата
Решение кв. уравнений по формулам
Решение кв. уравнений способом переброски
Решение кв. уравнений с помощью т.Виета
Решение кв. уравнений с использованием коэффициентом
Решение кв. уравнений графическим способом
Решение кв. уравнений с помощью циркуля и линейки
Решение кв. уравнений геометрическим способом
Решение кв. уравнений с помощью «номограмм»

Немного из истории…
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.
Квадратные уравнения в Древнем Вавилоне.
Квадратные уравнения в Индии.
Квадратные уравнения у ал - Хорезми.
Квадратные уравнения в Европе XIII - XVII вв.

Квадратные уравнения в Древнем Вавилоне.

Квадратные уравнения в Индии.

Квадратные уравнения у ал - Хорезми.

Квадратные уравнения в Европе XIII - XVII вв.

Знаменитый французский учёный Франсуа Виет(1540-1603) был по профессии адвокатом. Свободное время он посвящал астрономии. Занятия астрономией требовали знания тригонометрии и алгебры. Виет занялся этими науками и вскоре пришёл к выводу о необходимости их усовершенствования, над чем и проработал ряд лет.
Благодаря его труду, алгебра становится общей наукой об алгебраических уравнениях, основанной на буквенном исчислении. Поэтому стало возможным выражать свойства уравнений и их корней общими формулами.

При выполнении работы были замечены:
Способы которыми буду пользоваться:
Теорема Виета
Свойства коэффициентов
Метод «переброски»
Разложение левой части на множители
Графический способ
Способы интересные, но занимают много времени и не всегда удобны.
Графический способ
С помощью номограммы
Линейки и циркуля
Выделение полного квадрата
Преклоняюсь перед учеными которые открыли эти способы и дали науке толчок для развития в теме «Решение квадратных уравнений»

Разложение на множители левой части уравнения
Решим уравнение х2 + 10х - 24=0. Разложим на множители левую часть: х2 + 10х - 24= х2 + 12х -2х - 24= х(х + 12) - 2(х + 12)= (х + 12)(х - 2).
(х + 12)(х - 2)=0
х + 12=0 или х - 2=0
х= -12 х= 2
Ответ: х1= -12, х2 = 2.
Решить уравнения: х2 - х=0
х2 + 2х=0
х2 - 81=0
х2 + 4х + 3=0
х2 + 2х - 3=0

Метод выделения полного квадрата
Решим уравнение х2 + 6х - 7=0
х2 + 6х - 7=х2 + 2х3 + 32 - 32 - 7=(х-3)2 - 9- 7= (х-3)2 - 16
(х-3)2 -16=0
(х-3)2 =16
х-3=4 или х-3=-4
х=1 х=-7
Ответ: х1=1, х2 =-7.
Решить уравнения: х2 - 8х+15=0
х2 +12х +20=0
х2 + 4х + 3=0
х2 + 2х - 2=0
х2 - 6х + 8=0

Решение квадратных уравнений по формуле
Основные формулы:
Если b - нечетное, то D= b2-4ac и х 1,2= , (если D>0)
Если b- -четное, то D1= и х1,2= , (если D>0)
Решите уравнения: 2х2 - 5х + 2=0
6х2 + 5х +1=0
4х2 - 5х + 2=0
2х2 - 6х + 4=0
х2 - 18х +17=0
=

Решение уравнений способом переброски
Решим уравнение ах2 +bх+с=0. Умножим обе части уравнения на а, получим а2 х2 +аbх+ас=0. Пусть ах =у, откуда х = у/а. Тогда У2 +bу+ас=0. Его корни у1 и у2 . Окончательно х1 = у1 /а, х1 = у2 /а.
Решим уравнение 2х2 -11х + 15=0.
Перебросим коэффициент 2 к свободному члену:
У2 -11у+30=0.
Согласно теореме Виета у1 =5 и у2 =6.
х1 =5/2 и х2 =6/2
х1 =2,5 и х2 =3
Ответ: х1=2,5 , х2 =3
Решить уравнение: 2х2 -9х +9=0
10х2 -11х + 3=0
3х2 +11х +6=0
6х2 +5х - 6=0
3х2 +1х - 4=0

Решение уравнений с помощью теоремы Виета
Решим уравнение х2 +10х-24=0.
Так как х1 *х2 =-24
х1 +х2 = -10, то 24= 2*12, но -10=-12+2, значит
х1 =-12 х2 =2
Ответ: х1=2, х2 =-12.
Решить уравнения: х2 - 7х - 30 =0
х2 +2х - 15=0
х2 - 7х + 6=0
3х2 - 5х + 2=0
5х2 + 4х - 9=0

Свойства коэффициентов квадратного уравнения
Если a+b+c=0, то х2 = 1, х2 = с/а Если a – b + c=0, то х2 =-1, х2 = -с/а
Решим уравнение х2 + 6х - 7= 0 Решим уравнение 2х2 + 3х +1= 0
1 + 6 – 7 =0, значит х1=1, х2 = -7/1=-7. 2 - 3+1=0, значит х1= - 1, х2 = -1/2
Ответ: х1=1, х2 =-7. Ответ: х1=-1, х2 =-1/2.
Решить уравнения: 5х2 - 7х +2 =0 Решить уравнения: 5х2 - 7х -12 =0
11х2 +25х - 36=0 11х2 +25х +14=0
345х2 -137х -208=0 3х2 +5х +2=0
3х2 +5х - 8=0 5х2 + 4х - 1=0
5х2 + 4х - 9=0 х2 + 4х +3=0

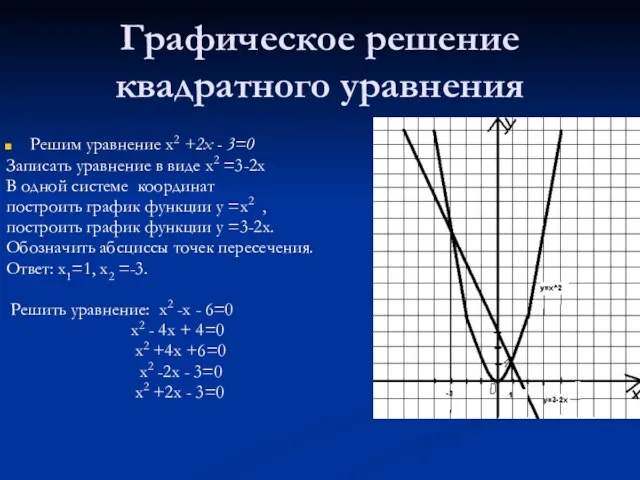
Графическое решение квадратного уравнения
Решим уравнение х2 +2х - 3=0
Записать уравнение в виде х2 =3-2х
В одной системе координат
построить график функции у =х2 ,
построить график функции у =3-2х.
Обозначить абсциссы точек пересечения.
Ответ: х1=1, х2 =-3.
Решить уравнение: х2 -х - 6=0
х2 - 4х + 4=0
х2 +4х +6=0
х2 -2х - 3=0
х2 +2х - 3=0

Решение уравнений с помощью циркуля и линейки
Решим уравнение aх2 +bх+c=0:
Построим точки S(-b:2a,(a+c):2a)- центр окружности и точку А(0,1)
Провести окружность радиуса SA
Абсциссы точек пересечения с осью Ох есть корни исходного уравнения

Геометрический способ решения уравнения
Решим уравнение у2 - 6у - 16=0
Представим в виде у2- 6у = 16. На рис.
«изображено» выражение у2- 6у , т.е.
из площади квадрата со стороной у
дважды вычитается площадь квадрата
со стороной 3. Значит у2 –6у+9 есть
площадь квадрата со стороной у-3.
Выполнив замену у2- 6у = 16, получим
(у-3)2 =16+9
у-3=5 или у-3=-5
у1 =8 у2 =-2 Решить уравнение у2 +6у - 16=0
Ответ: у1 =8 , у2 =-2