10 способов решения квадратных уравнений

Способ 1: разложение левой части уравнения на множители.
Решим уравнение
х2 + 10х - 24 = 0.
Разложим левую часть на множители:
х2 + 10х - 24 = х2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х - 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = - 12. Это означает, что число 2 и - 12 являются корнями уравнения х2 + 10х - 24 = 0.

Способ 2: метод выделения полного квадрата.
Решим уравнение х2 + 6х - 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2• х • 3.

В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как
х2 + 2• х • 3 + 32 = (х + 3)2.
Преобразуем теперь левую часть уравнения
х2 + 6х - 7 = 0,
прибавляя к ней и вычитая 32. Имеем:
х2 + 6х - 7 = х2 + 2• х • 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 - 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 - 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.

Способ 3: Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах2 + bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) - b2 + 4ac = 0,
(2ax + b)2 = b2 - 4ac,
2ax + b = ± √ b2 - 4ac,
2ax = - b ± √ b2 - 4ac,

Способ 4 : Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
x1 + x2 = - p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Например,
x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 > 0 и p = - 3 < 0;
x2 + 8x + 7 = 0; x1 = - 7 и x2 = - 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
Например,
x2 + 4x – 5 = 0; x1 = - 5 и x2 = 1, так как q= - 5 < 0 и p = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = - 1, так как q = - 9 < 0 и p = - 8 < 0.

Способ 5: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у2 + by + ас = 0,
равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета.
Окончательно получаем
х1 = у1/а и х1 = у2/а.

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример.
Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 – 11у + 30 = 0.
Согласно теореме Виета
у1 = 5 х1 = 5/2 x1 = 2,5
у2 = 6 x2 = 6/2 x2 = 3.
Ответ: 2,5; 3.

Способ 6: Свойства коэффициентов квадратного уравнения.
Пусть дано квадратное уравнение
ах2 + bх + с = 0, где а ≠ 0.
Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,
х2 = с/а.

Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x2 + b/a • x + c/a = 0.
Согласно теореме Виета
x1 + x2 = - b/a,
x1x2 = 1• c/a.
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x1 + x2 = - а + b/a= -1 – c/a,
x1x2 = - 1• ( - c/a),
т.е. х1 = -1 и х2 = c/a, что и требовалось доказать.

Примеры.
Решим уравнение 345х2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х1 = 1, х2 = c/a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
х1 = 1, х2 = c/a = 115/132.
Ответ: 1; 115/132.

Способ 7:Графическое решение квадратного уравнения.

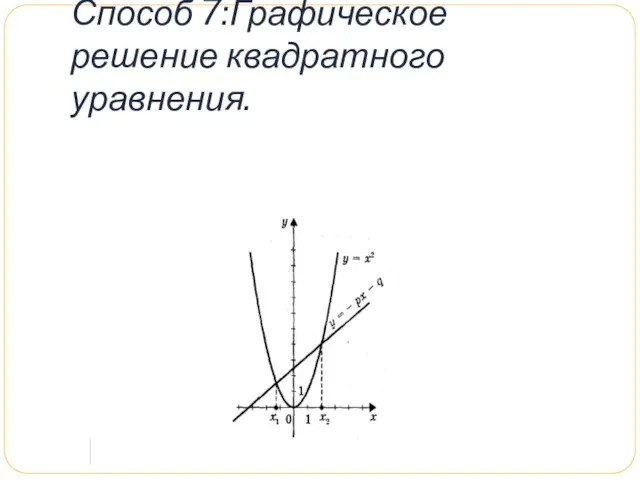
Если в уравнении
х2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
х2 = - px - q.
Построим графики зависимости у = х2 и у = - px - q.
График первой зависимости - парабола, проходящая через начало координат. График второй зависимости -
прямая .