10 способів знаходження НСЗ

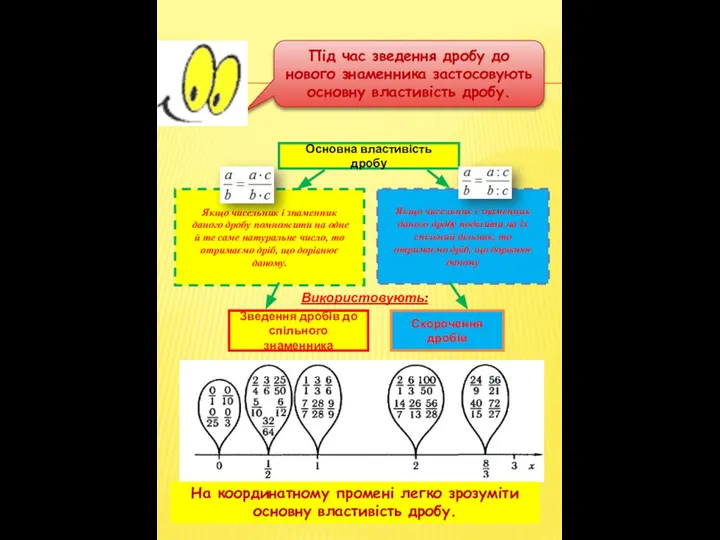
Якщо чисельник і знаменник даного дробу помножити на одне й те саме натуральне число, то отримаємо дріб, що дорівнює даному.
Якщо чисельник і знаменник даного дробу поділити на їх спільний дільник, то отримаємо дріб, що дорівнює даному
Зведення дробів до спільного знаменника
Основна властивість дробу
Використовують:
Скорочення
дробів
Під час зведення дробу до нового знаменника застосовують основну властивість дробу.
На координатному промені легко зрозуміти основну властивість дробу.

Будь-який дріб можна звести до нового знаменника.
Новим знаменником дробу може бути будь-яке кратне старого знаменника
Множення чисельника і знаменника на одне і теж натуральне число, відмінне від одиниці, називають зведенням дробу до нового знаменника.
А число, на яке множиться і чисельник і знаменник називають додатковим множником.

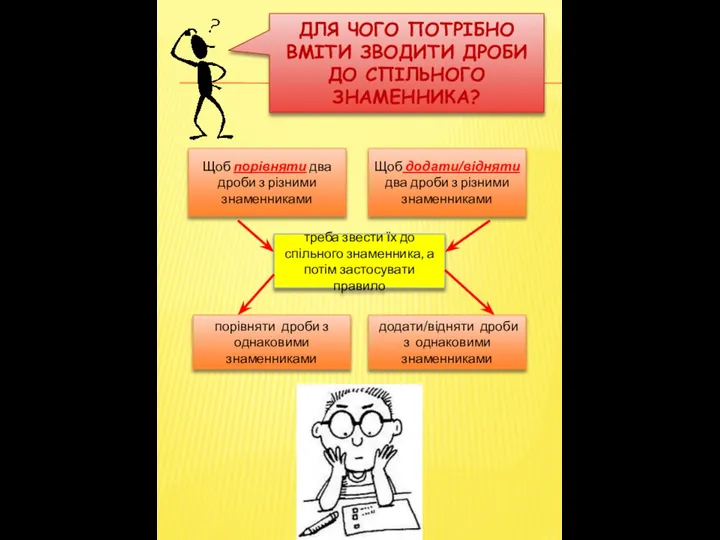
ДЛЯ ЧОГО ПОТРІБНО ВМІТИ ЗВОДИТИ ДРОБИ ДО СПІЛЬНОГО ЗНАМЕННИКА?
Щоб порівняти два дроби з різними знаменниками
Щоб додати/відняти два дроби з різними знаменниками
порівняти дроби з однаковими знаменниками
додати/відняти дроби з однаковими знаменниками
треба звести їх до спільного знаменника, а потім застосувати правило

Що означає звести дроби до спільного знаменника?
Будь-які два дроби можна звести до спільного знаменника.
Таким знаменником може бути будь-яке спільне кратне знаменників цих дробів. Зазвичай беруть найменше.
Найменший спільний знаменник =
найменшому спільному кратному
Згадай!
Найменшим спільним кратним двох чисел називається найменше число, яке ділиться на кожне з даних чисел.

Універсальний спосіб
Щоб звести дроби до найменшого
спільного знаменника, треба:
1) знайти найменше спільне кратне знаменників;
2) знайти додаткові множники для кожного дробу;
3) чисельник і знаменник кожного дробу помножити на відповідні додаткові множники.
Наприклад:
Спосіб знаходження НСЗ
Звести до спільного знаменнтка
дроби 1/6 і 3/8
и
.
Звести до спільного знаменнтка
дроби 3/4 і 5/6
1
2
Метод “найменшого спільного кратного”

Найпростіший і надійний спосіб, який гарантовано вирівнює знаменники. Будемо діяти «напролом»: множимо перший дріб на знаменник другого дробу, а другий - на знаменник першого В результаті знаменники обох дробів стануть рівними добутку вихідних знаменників. В якості додаткових множників беремо знаменники сусідніх дробів.
«Напролом»
Використовуючи саме цей метод - ви застрахуєте себе від безлічі помилок .
Єдиний недолік даного методу - доводиться багато обчислювати, в результаті можуть вийти дуже великі числа. Така розплата за надійність.
Наприклад
Найпростіший спосіб знаходження СЗ
Метод “метелика”
1
2
3
або

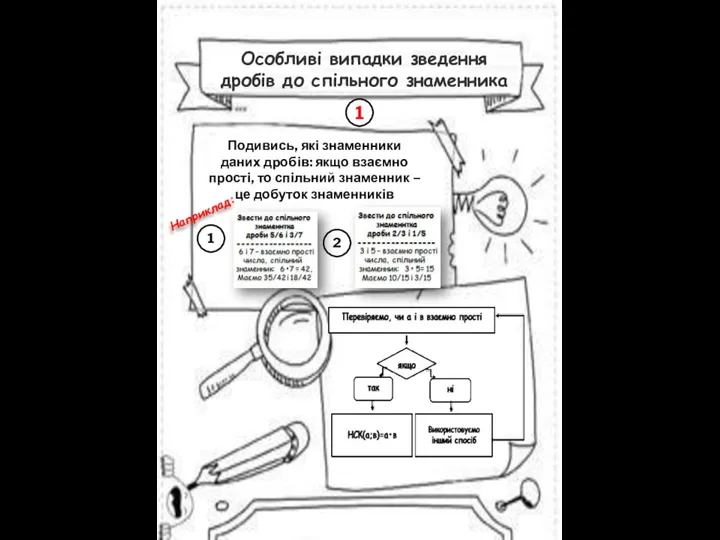
Особливі випадки зведення дробів до спільного знаменника
Наприклад:
Подивись, які знаменники
даних дробів: якщо взаємно прості, то спільний знаменник – це добуток знаменників
1
1
2

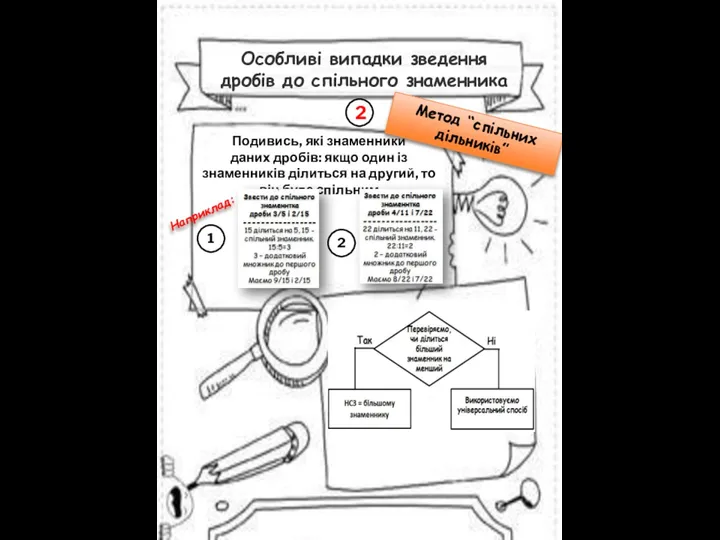
Особливі випадки зведення дробів до спільного знаменника
Подивись, які знаменники
даних дробів: якщо один із знаменників ділиться на другий, то він буде спільним
2
Наприклад:
1
2
Метод “спільних дільників”

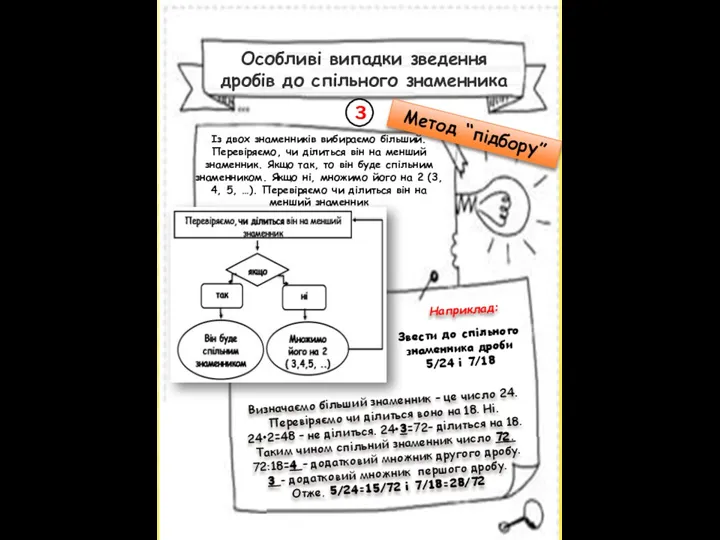
Особливі випадки зведення дробів до спільного знаменника
Із двох знаменників вибираємо більший. Перевіряємо, чи ділиться він на менший знаменник. Якщо так, то він буде спільним знаменником. Якщо ні, множимо його на 2 (3, 4, 5, …). Перевіряємо чи ділиться він на менший знаменник
Метод “підбору”
Визначаємо більший знаменник – це число 24. Перевіряємо чи ділиться воно на 18. Ні. 24•2=48 – не ділиться. 24•3=72– ділиться на 18.
Таким чином спільний знаменник число 72.
72:18=4 – додатковий множник другого дробу.
3 - додатковий множник першого дробу.
Отже, 5/24=15/72 і 7/18=28/72
Звести до спільного знаменника дроби 5/24 і 7/18
Наприклад:
3

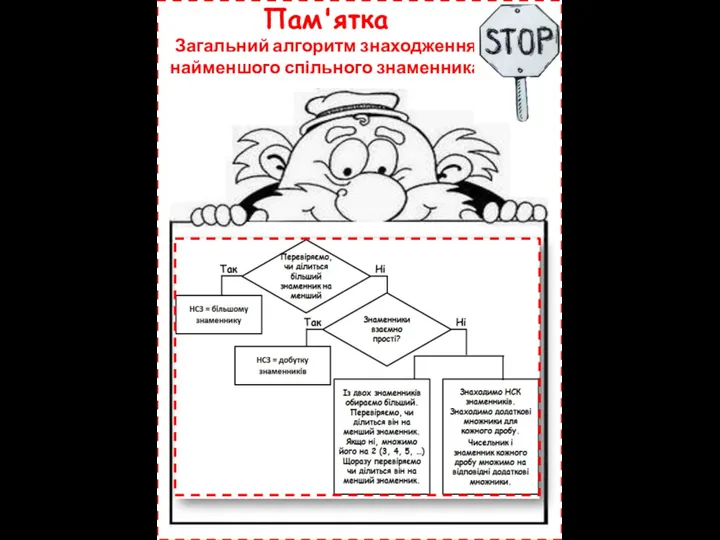
Пам'ятка
Загальний алгоритм знаходження найменшого спільного знаменника

Запишіть дроби 5/6 і 3/8 у вигляді дробів з найменшим спільним знаменником
-----------------
Кратні (6) = {12, 18,24, 30, …}
Кратні (8) = {8, 16,24, 32, …}
НОК (6, 8) = 24
Додатковий множник до першого дробу – 24:6=4
Додатковий множник до другого дробу - 24:8=3
Даний спосіб зазвичай застосовується для невеликих знаменників. Виписуємо в рядок кратні для кожного з чисел, поки не знайдеться кратне, однакове для обох
знаменників.
Приклад:
Ще спосіб!

Ще спосіб!
Знаходження
спільного знаменника
і додаткових множників розкладанням на прості множники знаменників даних дробів.
Приклад:

Ще спосіб!
Звести до спільного знаменнтка
дроби 1/8 і 5/12
-----------------
Створюєм із знаменників новий дріб.
Скорочуємо його до нескоротного.
Множимо: 8 х 3 = 12 х 2 = 24
НСК (8; 12) = 24
Приклад:
Множення «хрест-навхрест»

УВАГА!
Зводити до спільного знаменника можна не тільки два дроби, але й три, чотири і т.д.
Приклад:
Звести до найменшого спільного знаменника дроби
Розв’язання
Знайдемо НСК знаменників:
9 = 3 · 3;
18 = 3 · 3 · 2;
27 = 3 · 3 · 3.
НСК(9; 18; 27) = 3 · 3 · 2 · 3 = 54
Поділимо найменший спільний знаменник на знаменник кожного дробу і знайдемо додаткові
множники:
54 : 9 = 6; 54 : 18 = 3;
54 : 27 = 2.
Запишемо:

ЯК ОБЧИСЛЮЮТЬ НАЙМЕНШИЙ СПІЛЬНИЙ ЗНАМЕННИК
в Європі
у нас
НСЗ
НСК
Корисно знати
Сторінка-цікавинка
НСК (42, 70, 98)=2•3 •5 •7 •7=1470

Таємний спосіб
Як знайти спільний знаменник за допомогою таблиці множення

Чи немає якогось способу, що не потребує попереднього розкладання знаменників на прості множники?
Виявляється, є, і до того ж дуже простий. Потрібно перемножити знаменники і поділити знайдений добуток на їх НСД.
Знайти додаткові множники для кожного дробу. Чисельник і знаменник кожного дробу помножити на відповідні додаткові множники
Взаємозв’язок спільного знаменника з НСД