Содержание
- 2. Основные положения Комплексный чертеж точки Положение точки относительно плоскостей проекций План лекции
- 3. Основным элементом пространства принято считать точку, так как все геометрические фигуры можно представить как множество точек
- 4. В предыдущей лекции рассмотрена система двух плоскостей проекций (две взаимно перпендикулярные плоскости П1 и П2), показаны
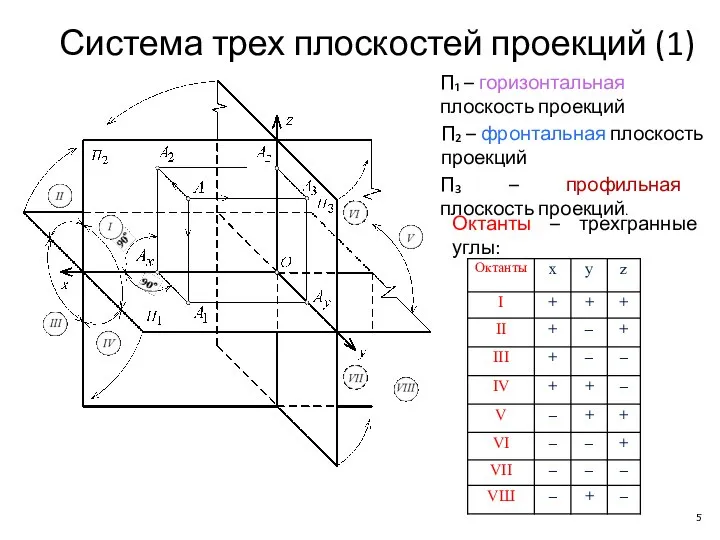
- 5. Система трех плоскостей проекций (1) П₁ – горизонтальная плоскость проекций П₂ – фронтальная плоскость проекций П₃
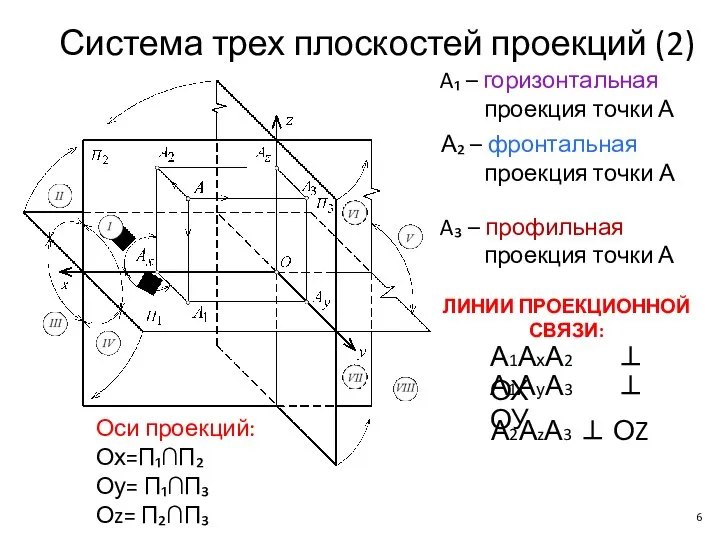
- 6. Система трех плоскостей проекций (2) A₁ – горизонтальная проекция точки А А₂ – фронтальная проекция точки
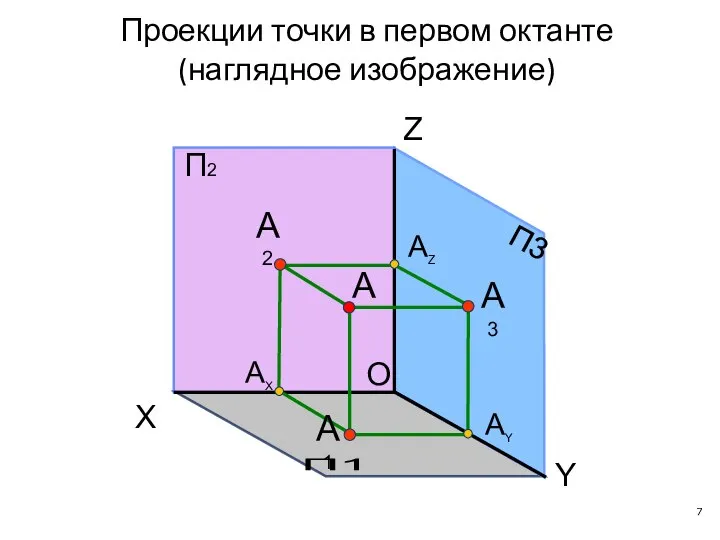
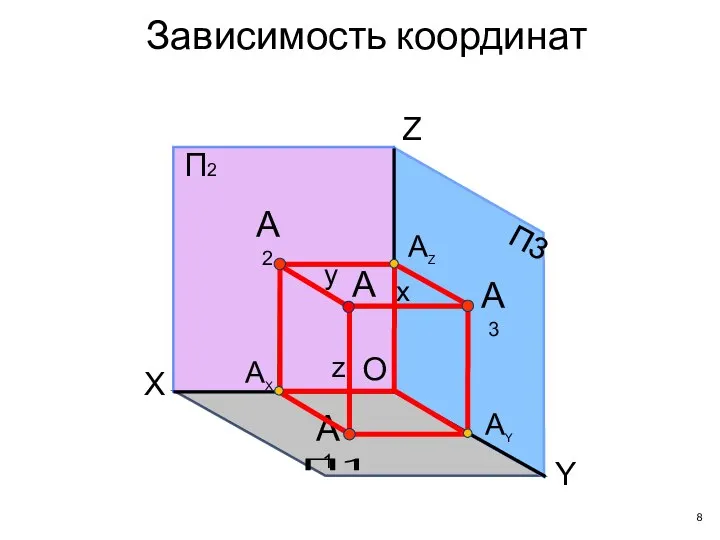
- 7. Проекции точки в первом октанте (наглядное изображение) O П2 П1 П3 X Y Z АX АY
- 8. O X Y Z АX АY А1 А А2 А3 АZ x y z П2 П1
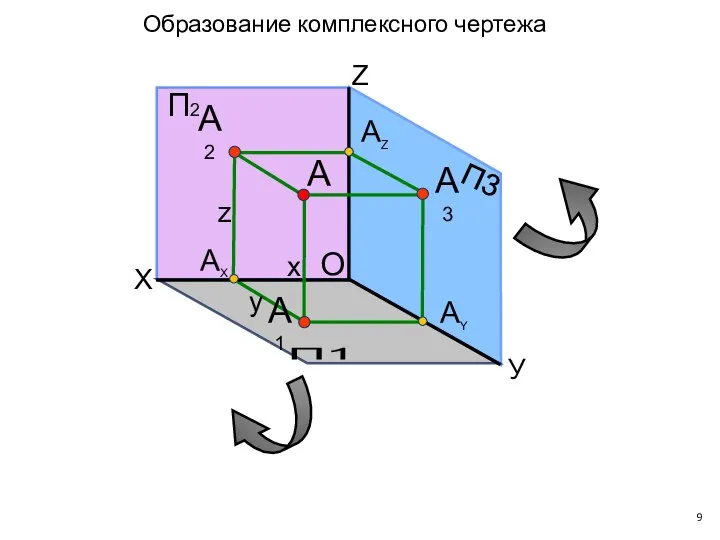
- 9. П2 П1 П3 X Z АX АY А1 А А2 А3 АZ O x y z
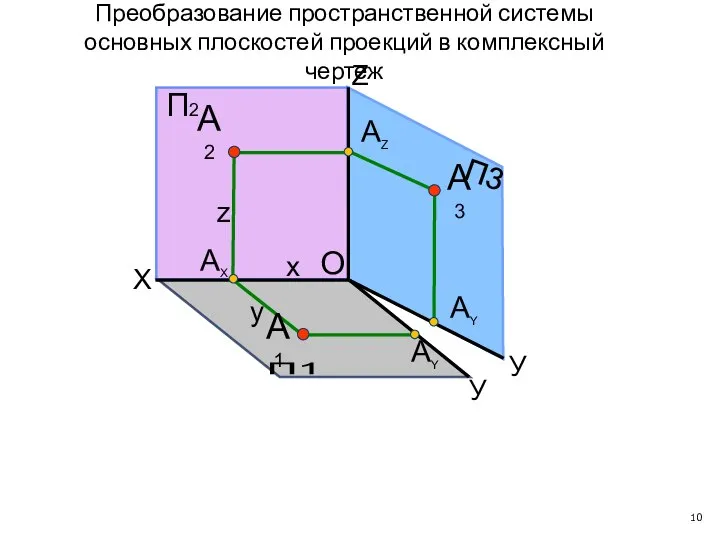
- 10. АY А1 А3 АY П1 П3 X У У АZ П2 Z А2 АX O x
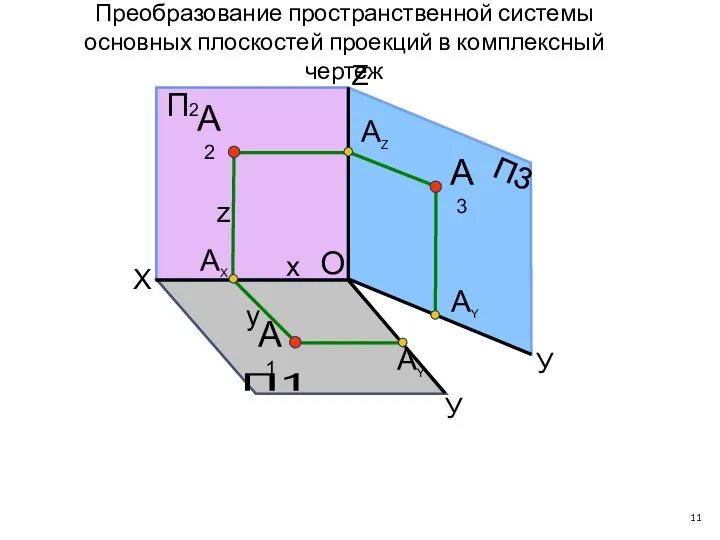
- 11. П1 П3 X У У O АY А1 А3 АY АX АZ П2 Z А2 x
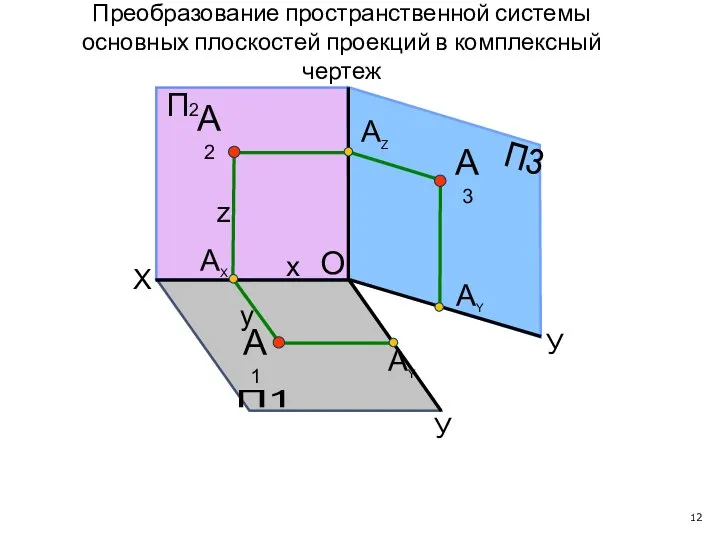
- 12. П1 П3 X У У АY А1 А3 АY АX АZ П2 А2 x y z
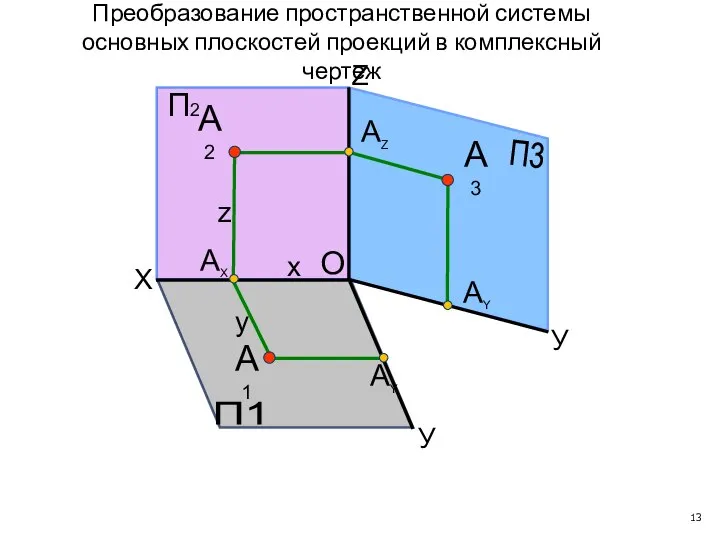
- 13. X У У П1 П3 АY А1 А3 АY АX АZ П2 Z А2 x y
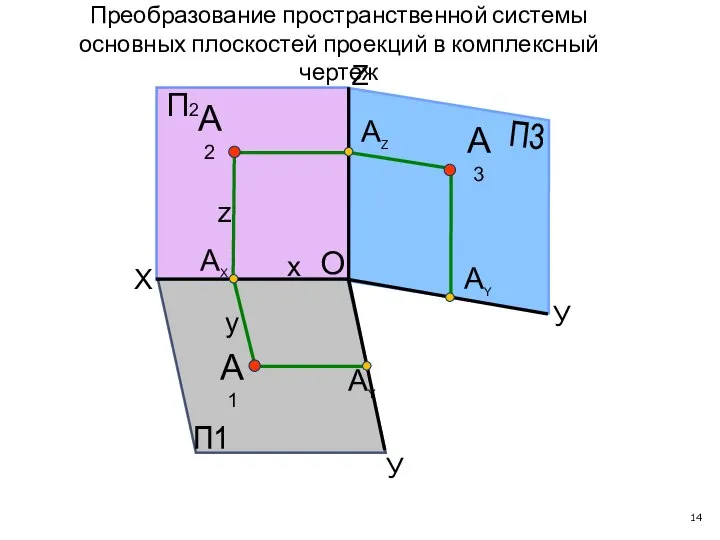
- 14. X У У П1 П3 АY А1 А3 АY АX АZ П2 Z А2 x y
- 15. X У У АY А1 АY АX АZ П2 Z А2 П1 П3 А3 x y
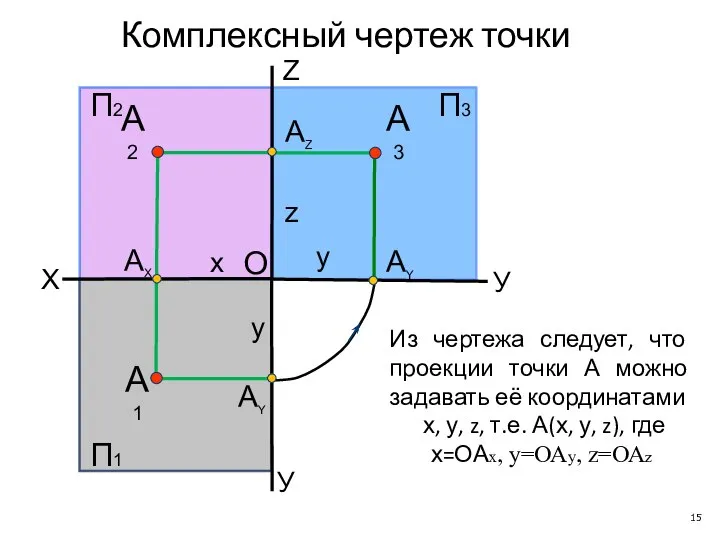
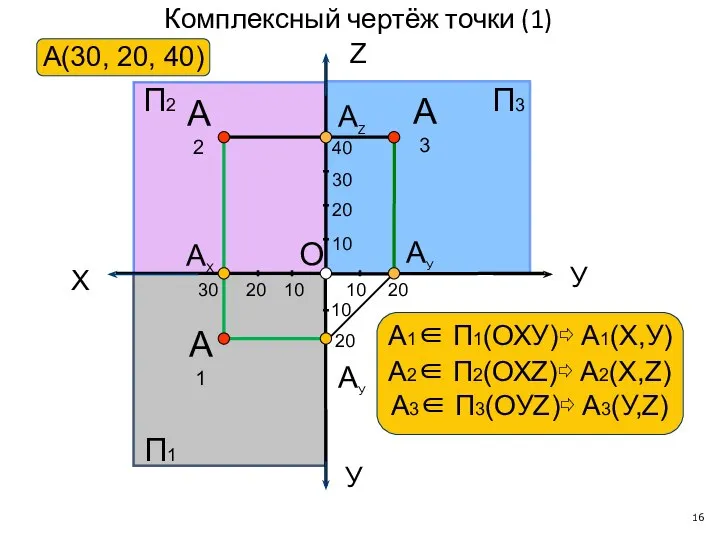
- 16. Комплексный чертёж точки (1) X У У АУ А1 АУ АX АZ П2 Z А2 П1
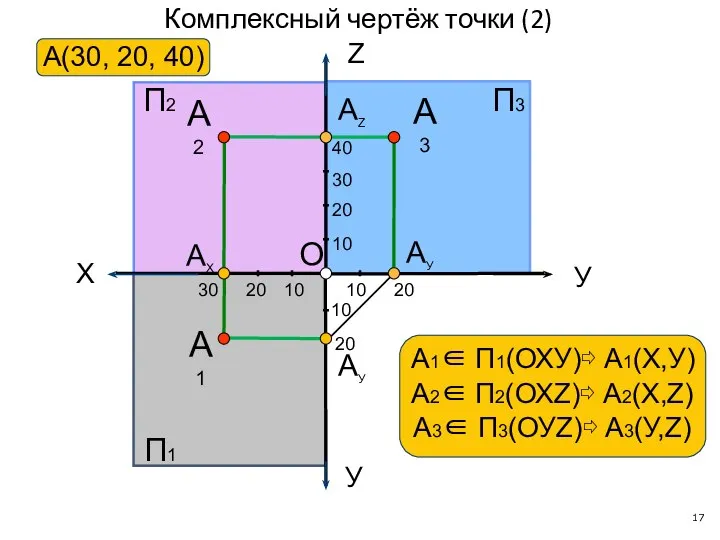
- 17. Комплексный чертёж точки (2) X У У АУ А1 АУ АX АZ П2 Z А2 П1
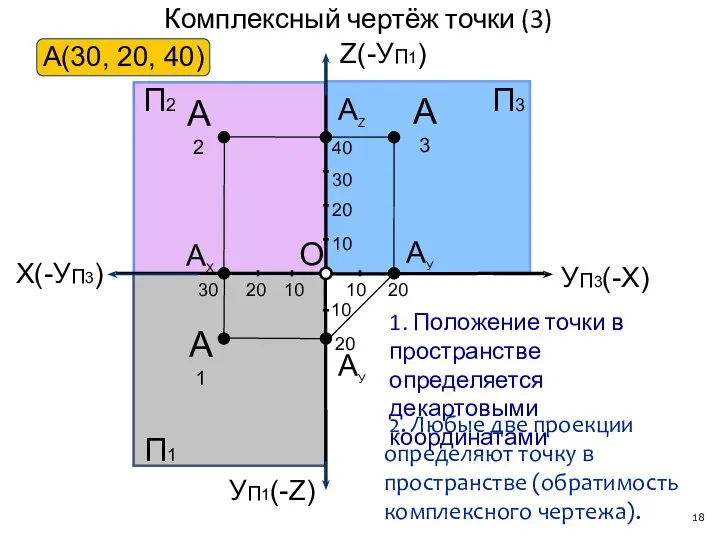
- 18. Комплексный чертёж точки (3) X(-УП3) УП3(-X) УП1(-Z) АУ А1 АУ АX АZ П2 Z(-УП1) А2 П1
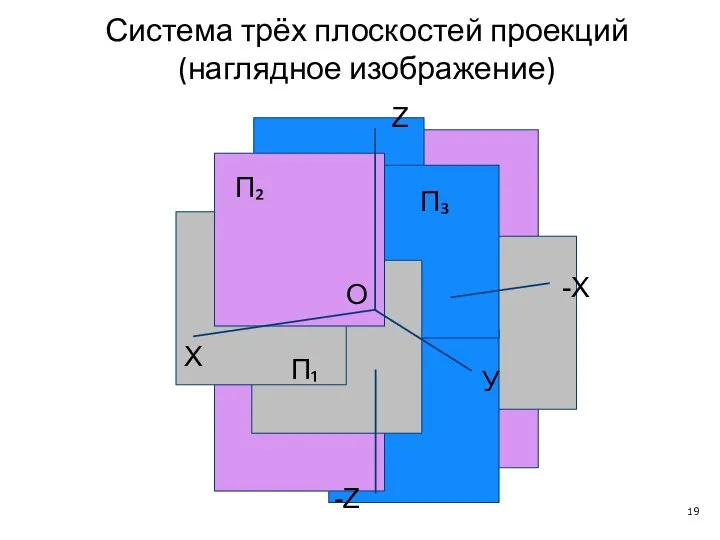
- 19. Система трёх плоскостей проекций (наглядное изображение) X У -X Z O -Z П₂ П₃ П₁
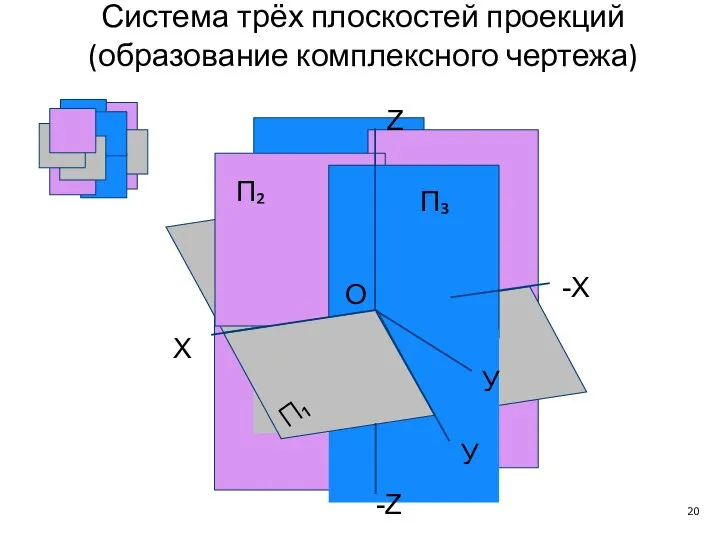
- 20. П₂ П₃ П₁ X У -X -Z O У Z Система трёх плоскостей проекций (образование комплексного
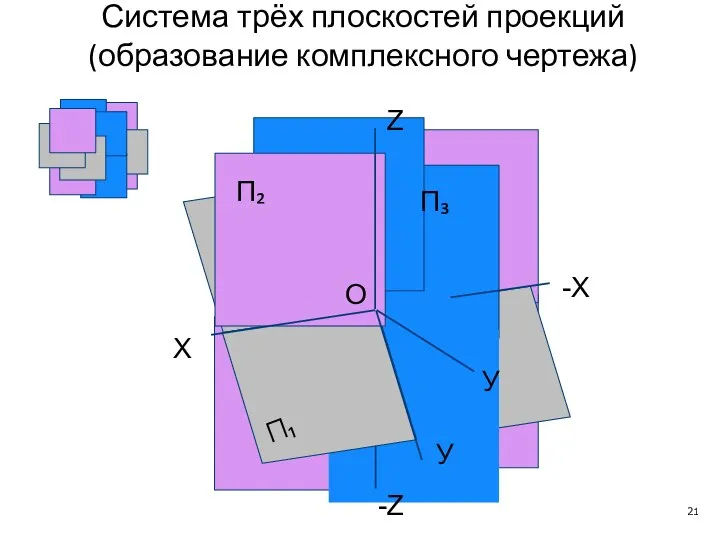
- 21. П₃ П₂ П₁ X -X O Z У У -Z Система трёх плоскостей проекций (образование комплексного
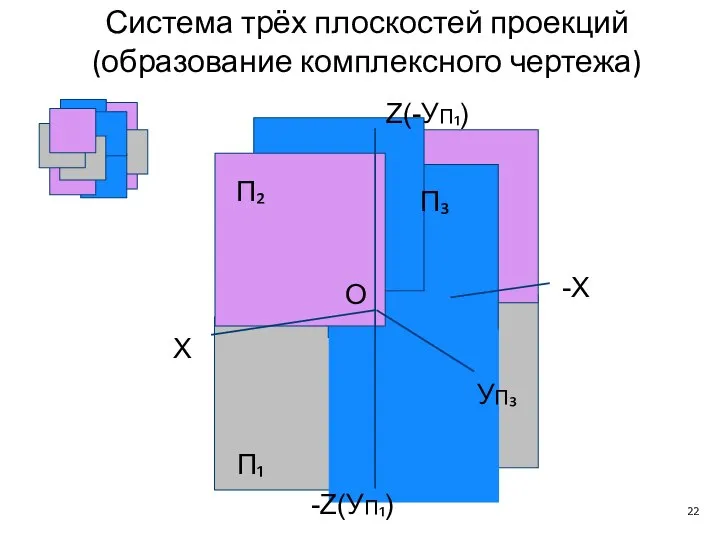
- 22. П₂ П₃ П₁ X -X O УП₃ -Z(УП₁) Z(-УП₁) Система трёх плоскостей проекций (образование комплексного чертежа)
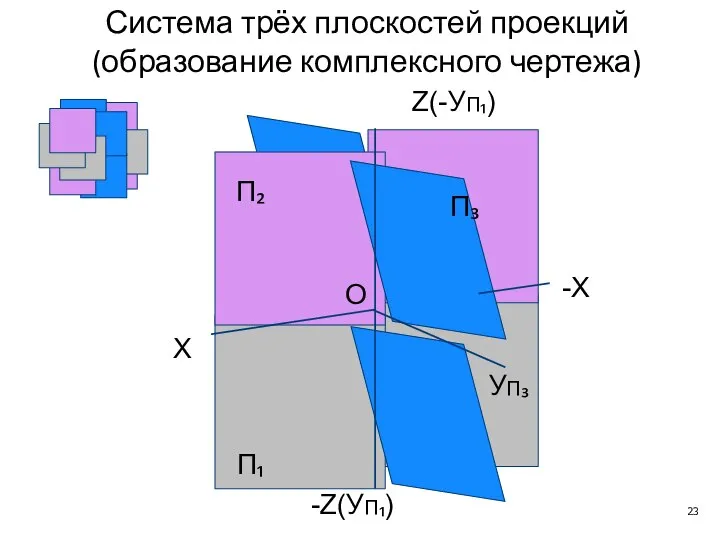
- 23. X -X O УП₃ Z(-УП₁) -Z(УП₁) П₂ П₁ П₃ Система трёх плоскостей проекций (образование комплексного чертежа)
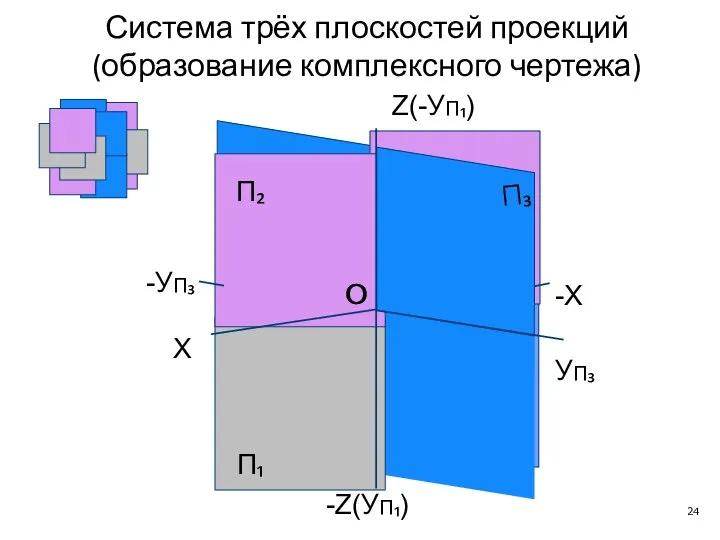
- 24. П₃ П₂ П₁ X -X O УП₃ -УП₃ O Z(-УП₁) -Z(УП₁) Система трёх плоскостей проекций (образование
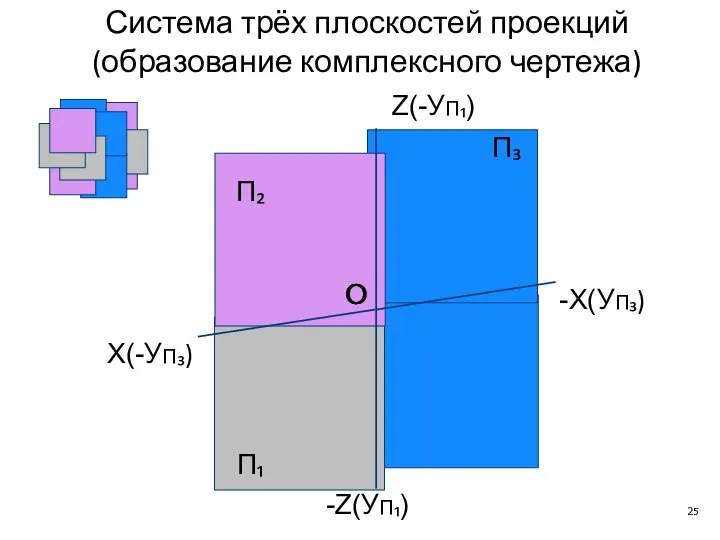
- 25. X(-УП₃) O -X(УП₃) Z(-УП₁) -Z(УП₁) O O П₂ П₁ П₃ Система трёх плоскостей проекций (образование комплексного
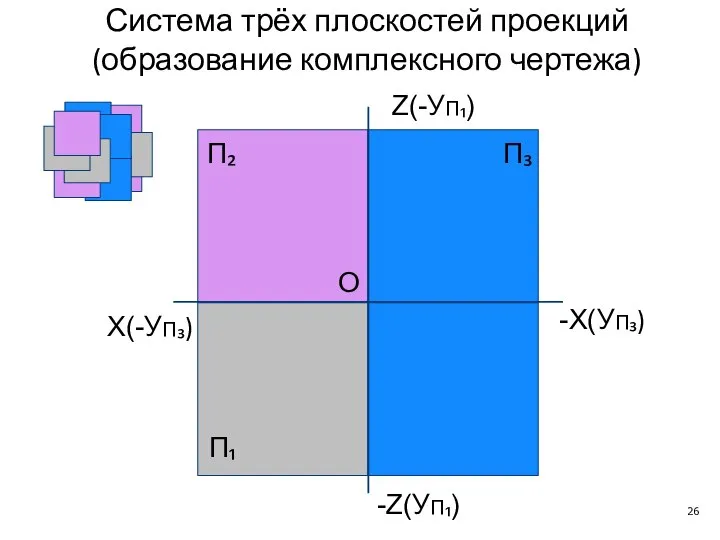
- 26. X(-УП₃) П₂ П₁ П₃ -X(УП₃) O Z(-УП₁) -Z(УП₁) Система трёх плоскостей проекций (образование комплексного чертежа)
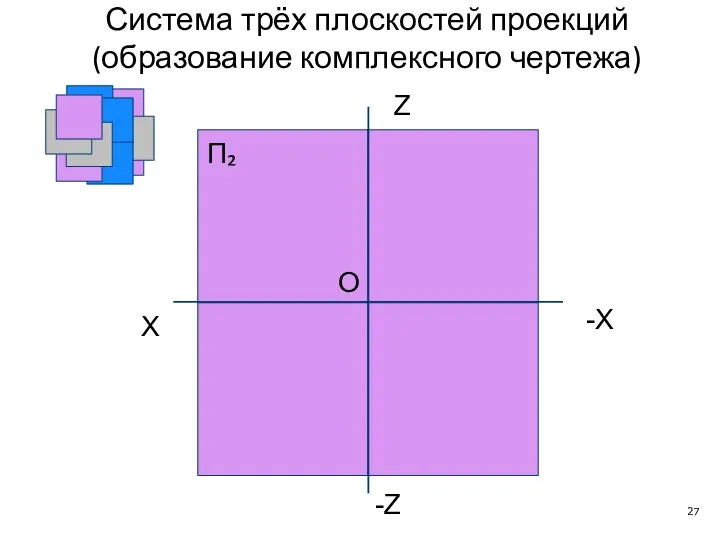
- 27. X П₂ -X O Z -Z Система трёх плоскостей проекций (образование комплексного чертежа)
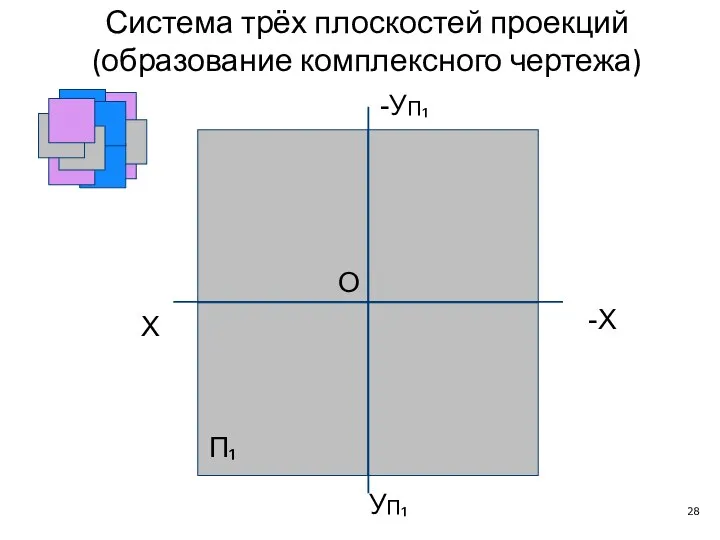
- 28. X П₁ -X O -УП₁ УП₁ Система трёх плоскостей проекций (образование комплексного чертежа)
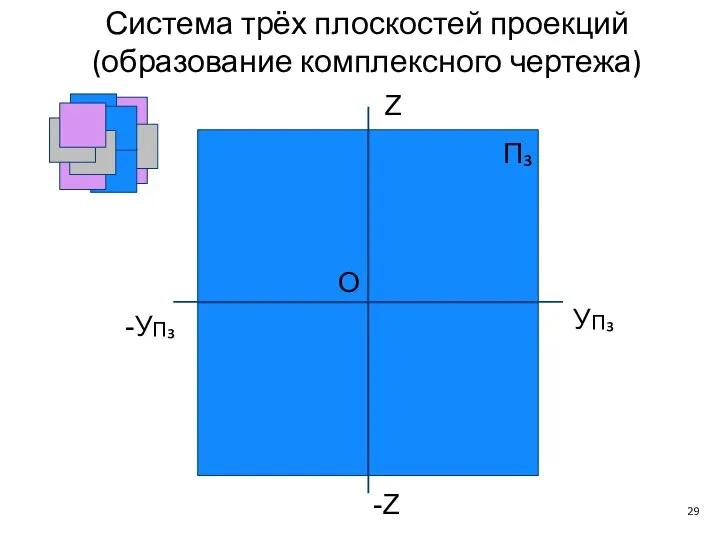
- 29. -УП₃ П₃ УП₃ O Z -Z Система трёх плоскостей проекций (образование комплексного чертежа)
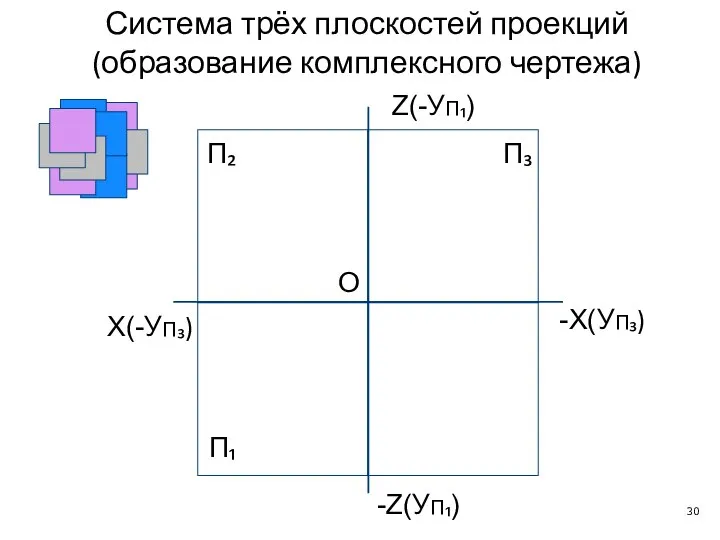
- 30. X(-УП₃) П₂ П₁ П₃ -X(УП₃) O Z(-УП₁) -Z(УП₁) Система трёх плоскостей проекций (образование комплексного чертежа)
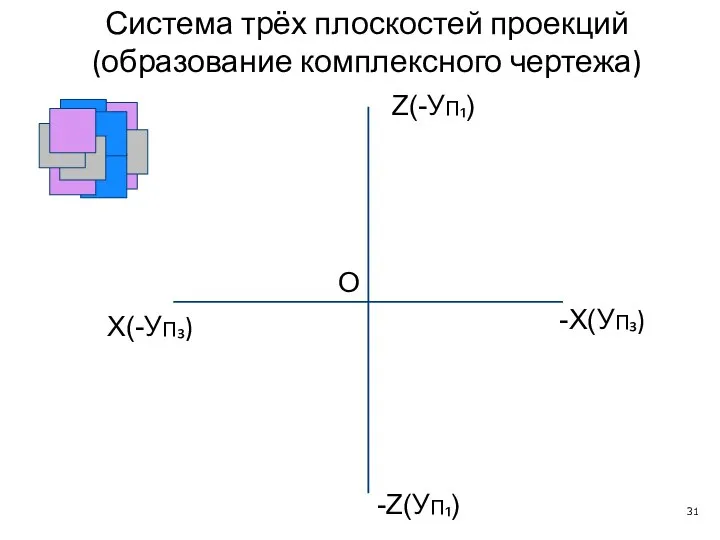
- 31. X(-УП₃) -X(УП₃) O Z(-УП₁) -Z(УП₁) Система трёх плоскостей проекций (образование комплексного чертежа)
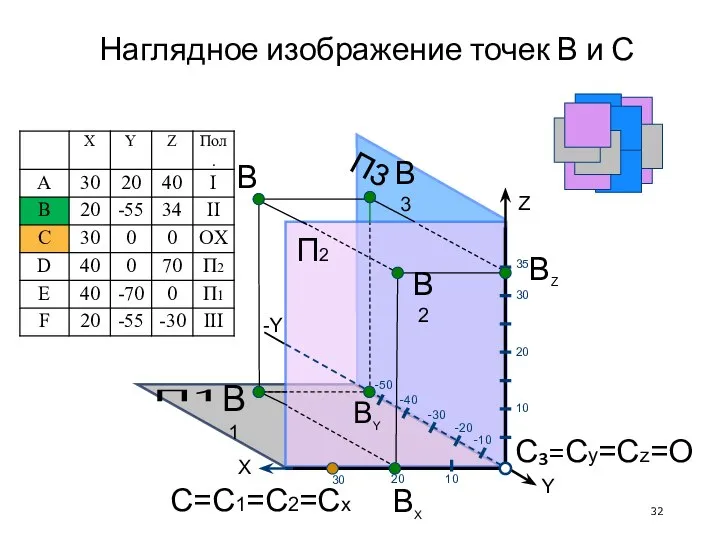
- 32. Наглядное изображение точек В и С С₃=Cy=Cz=O П2 П1 П3 X -Y Z ВX ВY В1
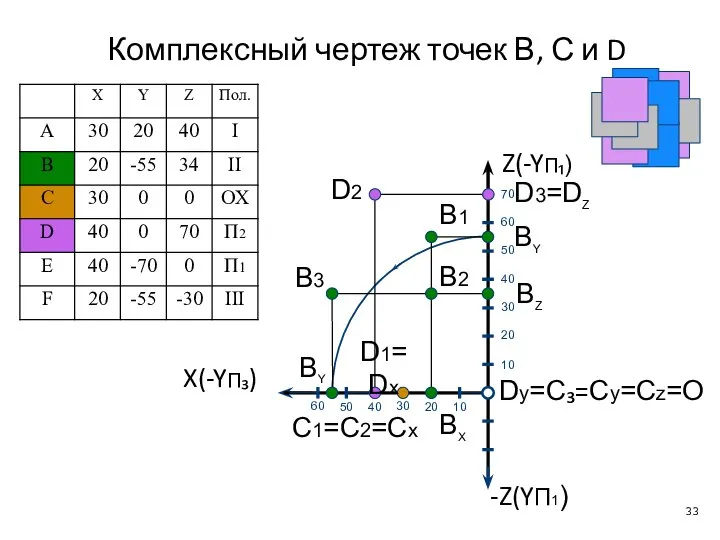
- 33. Комплексный чертеж точек В, С и D Dy=С₃=Cy=Cz=O X(-YП₃) Z(-YП₁) ВX ВY В1 В2 В3 ВZ
- 35. Скачать презентацию


 Модели ствола скважины
Модели ствола скважины Человек в обществе
Человек в обществе Наши мальчики
Наши мальчики Концепция воспитания в системе непрерывного образования Республики Казахстан
Концепция воспитания в системе непрерывного образования Республики Казахстан Теория государства и права и антропология. Юридическая антропология
Теория государства и права и антропология. Юридическая антропология Учебный план. Родительское собрание. 3 класс
Учебный план. Родительское собрание. 3 класс Тема лекции: договор транспортной экспедиции
Тема лекции: договор транспортной экспедиции HISTORY OF ENGLISH I
HISTORY OF ENGLISH I «Искусственный шелк»
«Искусственный шелк» Совещание заместителей директоров по УВР
Совещание заместителей директоров по УВР Цель программы Цель программы – выявление интересных идей в сфере рекламного бизнеса. Задачи программы: 1.Стимулирование творческ
Цель программы Цель программы – выявление интересных идей в сфере рекламного бизнеса. Задачи программы: 1.Стимулирование творческ Механика(обобщающее занятие)
Механика(обобщающее занятие) Конвенция о правах ребенка и реалии детства в современной России
Конвенция о правах ребенка и реалии детства в современной России Геральдика стран Европы
Геральдика стран Европы Клуб исторической реконструкции Чертог Раса
Клуб исторической реконструкции Чертог Раса Результаты итоговой аттестации выпускников 9 классов 2009-2010 учебного года, сдававших экзамены в новой форме :
Результаты итоговой аттестации выпускников 9 классов 2009-2010 учебного года, сдававших экзамены в новой форме : Lifting and Moving Victims
Lifting and Moving Victims Запятая и точка с запятой в бессоюзном сложном предложении
Запятая и точка с запятой в бессоюзном сложном предложении Презентация по изо на тему _Звери в лесу_ (2 класс) (1)
Презентация по изо на тему _Звери в лесу_ (2 класс) (1) Великие реформы Александра II (1855 -1881)
Великие реформы Александра II (1855 -1881) Лекция 3. new
Лекция 3. new Презентация на тему Как животные готовятся к зиме
Презентация на тему Как животные готовятся к зиме  Научная работа «Глушение скважин в условиях АНПД. Эффективность внедрения технологических растворов для ремонта скважин на осно
Научная работа «Глушение скважин в условиях АНПД. Эффективность внедрения технологических растворов для ремонта скважин на осно Пултрузия как технологический процесс
Пултрузия как технологический процесс Предварительный перечень конкурсов по 7РП в 2012 году
Предварительный перечень конкурсов по 7РП в 2012 году Manual Local Ticketingверсия 2.11
Manual Local Ticketingверсия 2.11 НАПРАВЛЕНИЯ РАЗВИТИЯ ПРИРОДООХРАННОЙ ДЕЯТЕЛЬНОСТИНА МУНИЦИПАЛЬНОМ УРОВНЕ
НАПРАВЛЕНИЯ РАЗВИТИЯ ПРИРОДООХРАННОЙ ДЕЯТЕЛЬНОСТИНА МУНИЦИПАЛЬНОМ УРОВНЕ Типы икон Богоматери и Христа
Типы икон Богоматери и Христа