20151007_matematika

Биология и математика – что может быть общего у этих столь различных областей знания?
Важная роль математики в таких точных науках, как физика, общепризнана, однако ценность и целесообразность применения математических методов в менее «строгих» науках, например биологии, нередко ставится под сомнение. В большинстве случаев биологический материал живой природы крайне изменчив и многообразен, подвержен влиянию многочисленных сложных факторов – поэтому точный математический анализ в этой области многие ученые считали невозможным.

Однако еще древние мыслители считали математику основополагающей дисциплиной. Галилео Галилей сказал: «Математика – это язык, на котором написана книга природы». Широко известен и афоризм Карла Гаусса: «Математика – царица наук».
Математика – это чрезвычайно мощный и гибкий инструмент изучения окружающего нас мира. В любой научной дисциплине существует своя методология, основанная на выполнении конкретных экспериментов. Эти сведения фиксируются и обрабатываются в виде чисел. Обработкой числовой информации занимается математика, что свидетельствует о её непосредственной связи с другими науками.

Первый крупный математик средневе-ковой Европы Леонардо Пизанский, или Фибоначчи (1170 – 1250), прославился своей знаменитой задачей, сформулированной в биологической постановке. Это задача о популяции кроликов, которые начинают размножаться со второго месяца после своего рождения и каждый месяц дают потомство в виде новой пары кроликов. В итоге получается числовая последова-тельность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …, где каждое следующее число является суммой двух предыдущих. Этот ряд получил название «числа Фибоначчи».

Числовой ряд Фибоначчи иллюстративно выражается в виде спирали, увеличение шага которой всегда равномерно. Спиральные формы широко встречаются в природе – в раковине моллюска, во многих цветах и растениях. Есть предположение, что ряд Фибоначчи – это попытка природы адаптиро-ваться к более фундаментальной и совершен-ной логарифмической последовательности.

Леонардо да Винчи (1452 – 1519), итальянский художник, ученый и изобретатель, обогатил мировоззрение эпохи Возрождения идеей ценности математики: «Никакое человеческое исследование не может быть названо истинной наукой, если оно не прошло через математические доказательства».
Изучая анатомию человеческого тела и функции органов, а также движение человека и животных, Леонардо рассматривал организм как образец «природной механики». В своих записях он подчеркивал необходимость знания геометрии, представления перспективы, метода расчета силы и крепости мышц.

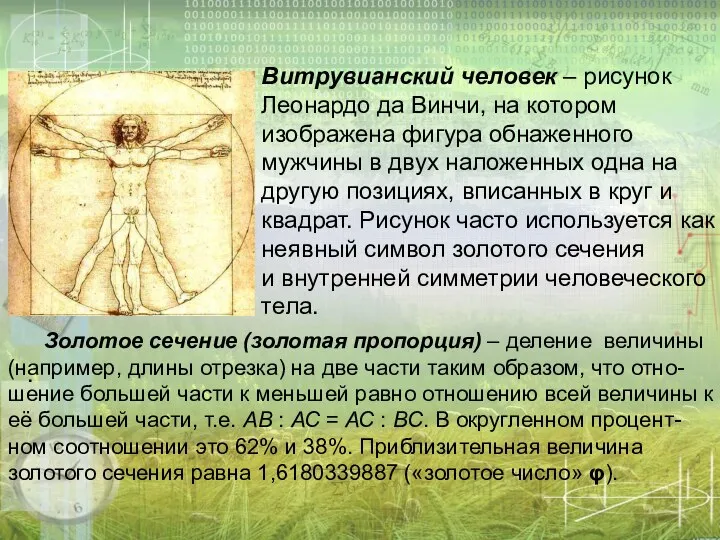
Витрувианский человек – рисунок Леонардо да Винчи, на котором изображена фигура обнаженного мужчины в двух наложенных одна на другую позициях, вписанных в круг и квадрат. Рисунок часто используется как неявный символ золотого сечения и внутренней симметрии человеческого тела.
.
Золотое сечение (золотая пропорция) – деление величины (например, длины отрезка) на две части таким образом, что отно-шение большей части к меньшей равно отношению всей величины к её большей части, т.е. АВ : АС = АС : ВС. В округленном процент-ном соотношении это 62% и 38%. Приблизительная величина золотого сечения равна 1,6180339887 («золотое число» φ).

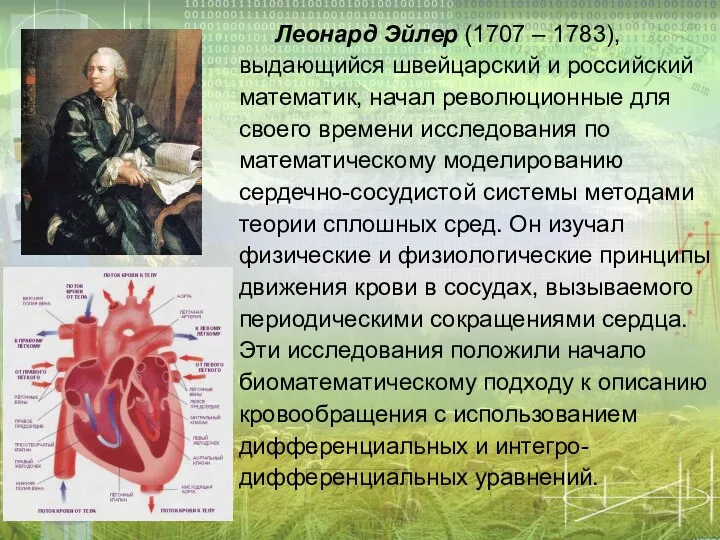
Леонард Эйлер (1707 – 1783), выдающийся швейцарский и российский математик, начал революционные для своего времени исследования по математическому моделированию сердечно-сосудистой системы методами теории сплошных сред. Он изучал физические и физиологические принципы движения крови в сосудах, вызываемого периодическими сокращениями сердца. Эти исследования положили начало биоматематическому подходу к описанию кровообращения с использованием дифференциальных и интегро-дифференциальных уравнений.
.

Томас Мальтус (1766 – 1854), английский демограф и экономист, создал теорию неконтролируемого роста человеческой популяции на Земле, согласно которой народонаселение растет в геометрической прогрессии, а средства существования – в арифметической. С современной точки зрения данная теория имеет целый ряд недостатков, однако
.
идеи Мальтуса оказали мощное позитивное воздействие на развитие математических моделей популяционной биологии, а также этнологии и экологии.

Грегор Иоганн Мендель (1822 – 1884), австрийский биолог, был в числе немногих, кто в середине XIX в. применил алгебраиче-ские формулы для анализа гибридизации растений. Количественный учёт всех типов полученных гибридов, а также вариационно-статистический подход, характерный для всего склада мышления ученого, позволили ему впервые обосновать и сформулировать закономерности свободного расхождения и комбинирования наследственных факторов. Эти закономерности, получившие название законов Менделя, легли в основу учения о наследственности и стали первым шагом на пути к современной генетике.
.

Герман Гельмгольц (1821 – 1894), немецкий биофизик, впервые дал математическое обоснование закона сохранения энергии, показал всеобщность этого закона, его распространение на происходящие в живых организмах процессы. Он изучил процесс мышечного сокращения, обнаружил и измерил теплообразование в мышце, скорость распространения возбуждения в нервах, определил скрытый период рефлексов. Гельмгольц исследовал некоторые уравнения математической физики в связи со своими фундаментальными работами по физиологии зрения и слуха.

Таким образом, отдельные ученые исследовали биологические проблемы, представляющие интерес с математической точки зрения. В то же время биология посте-пенно превращалась из науки наблюдательной в науку экспериментальную. До середины XIX века ученый-естествоиспытатель своей основной задачей считал наблюдение за живыми организмами, описание и систематизацию всего их многообразия.
В XX веке биологи всё глубже и интенсивнее вторгались в область эксперимента. В результате было накоплено большое количество фактов той степени точности и абстрактности, кото-рая допускает применение математического аппарата, и это нашло отражение в специальной литературе (Дж.Смит и др.).

Особого внимания заслуживают научные труды Нормана Бейли «Статистические методы в биологии» и «Математика в биологии и медицине», опубликованные в 1960 – 70-е годы XX века. В этих работах освещалась методология применения различ-ных разделов математики в экспериментальных исследованиях по биологии. В них также проводился математический анализ конкретных биологических и медицинских проблем, в частности медицинской диагностики, моделей генетического сцепления, распространения эпидемий и роста численности популяций.

Основные закономерности проникновения математики в биологию:
развитие теории вероятностей и методов математической статистики (для планирова-ния и обработки результатов экспериментов);
использование математики как средства моделирования биологических систем (биологические системы часто описываются дифференциальными или интегральными уравнениями).

Активное использование в биологии методов математической статистики привело к формиро-ванию целого научного направления (Р. Фишер) – биометрии. Данный раздел биологии изучает наследственность, изменчивость и ряд других биологических явлений, связанных с выражением жизненных процессов в количественном виде. Проникая своим методом «числа и меры» в самые разнообразные области биологических знаний, биометрия осуществляет завет Галилея: измерять всё измеримое и делать измеримым то, что пока еще не поддается измерению.
В современном мире под биометрией понимается также совокупность автоматических методов распознавания физиологических характеристик человека с целью его идентификации (сканирова-ние сетчатки глаза, дактилоскопия, распознавание голоса, цифровая фотография и др.).

Генетика – наука о законах наследственности и изменчивости организмов; наиболее математи-зированная из всех биологических дисциплин. Основы современной генетики были заложены еще Г. Менделем, а в ХХ веке решающее значе-ние для её развития имело открытие «вещества наследственности» – дезоксирибонуклеиновой кислоты (ДНК) и генетического кода.
Статистические (биометрические) методы играют важную роль в расшифровке генетического кода (определенных сочетаний нуклеотидов и последовательности их расположения в молекуле ДНК), а также в составлении хромосомных карт. Без этих математически точных методов невозможно достоверно установить характер передачи наследственной информации.
Генетика в настоящее время по праву считается одной из самых важных областей не только биологии, но и всей науки, определяющей развитие человечества.

Важную роль в математизации биологии сыграло обращение к принципам кибернетики, идеям теории регулирования и теории информации. Существенно изменился подход к пониманию регуляторных биологических систем, основ реализации обратных связей. Биологическая кибернетика в целом занимается изучением общих вопросов передачи, переработки и хранения информации в живых системах. Биокибернетический подход оказался особенно плодотворным в исследовании процессов жизнедеятельности клеток, морфогенеза, работы мозга и органов чувств, генетической структуры популяций, коммуникации между животными, экологических проблем.
Норберт Винер, основоположник кибернетики
Анохин П.К., выдающийся физиолог, создатель теории функциональных систем

В ХХ веке на службу биологии были «приняты» и алгебра, и кибернетика, и теория вероятностей, и математическая статистика, и дифференциальное и интегральное исчисление, и топология, и теория конечных автоматов. Поэтому с полным основанием можно говорить о возникновении особой научной отрасли, представляющей собой интеграцию теорети-ческой биологии и прикладной математики, – математической биологии.
Математическая биология – это теория математических моделей биологических процессов и явлений, которая занимается проблемами роста организмов, развитием образцов, статистикой роста населения, распространением болезней. Критерием истины в ней является математическое доказательство, имеющее биологическую интерпретацию.

«Значение математики сейчас непрерывно возрастает. В математике рождаются новые идеи и методы. Всё это расширяет сферу её приложения. Сейчас уже нельзя назвать такой области деятельности людей, где математика не играла бы существенной роли. Она стала незаменимым орудием во всех науках о природе, в технике, в обществоведении. Даже юристы и историки берут на своё вооружение математические методы».
А. Д. Александров (1912 – 1999),
выдающийся петербургский математик,
академик АН СССР, обладатель Золотой медали имени Эйлера.

Таким образом, процесс интеграции математики и биологии имеет длительную историю. Биология как источник новых моделей, как наука, изучающая объекты, которые не имеют аналогов в физике и технике, и потому позволяющая ставить совершенно новые задачи, привлекает к себе внимание многих выдающихся математиков. В свою очередь математика не только проникает в биологию и ранее чуждые для неё области, «завоё-вывает» их, но и сама при этом трансформируется, становится менее формальной, меняет свои методологические черты, приближаясь в какой-то степени к наукам гуманитарным.