Построение начального курса математики

Построение курса математики отличается следующим особенностями:
Основой начального курса математики является арифметика натуральных чисел и основных величин, в курс включены также вопросы алгебры, геометрии и работы с информацией.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
В составлении учебных программ и учебников возможны два варианта построения их содержания:
а) линейное
б) концентрическое
Концентрическое построение материала предложил Петр Семенович Гурьев (1807–1887) в своей работе «Практическая арифметика» в 1861 г. В основу такого построения кладется изучение по расширяющимся кругам.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
При линейном построении все время осуществляется переход к новому материалу.
Каждый предыдущий материал является основой для следующего, причем, благодаря наличию смысловой зависимости, последующий материал зависит от предыдущего. Такое построение наиболее часто встречается в программах и учебниках для старших классов.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
При концентрическом построении курса одинаковый учебный материал вводится поочередно на разных уровнях обучения. Каждый из этих уровней составляет определенный цикл, или, назовем, концентр. Первоначальный концентр содержит лишь наиболее важные положения, которые в последующих концентрах излагаются более подробно, полно. Такой подход намного облегчает запоминание и понимание, а также овладение математическими навыками и мышлением.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Обучение математике начинается с небольшой области чисел, доступной детям и известной им до школы, эта область чисел постепенно расширяется и вводятся новые понятия; при таком построении курса обеспечивается систематическое повторение и вместе с тем углубление изученного, так как полученные ранее знания, умения и навыки находят применение в новой области чисел. Все это способствует лучшему усвоению курса.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Методическое обоснование концентрического расположения материала (преимущества):
– соблюдается переход от простого к сложному;
– в каждом концентре идет повторение изученного, предыдущего и дополняется новым;
– есть возможность вносить в работу необходимое разнообразие;
– есть возможность совместного изучения взаимообратных действий.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Психологическое обоснование концентрического расположения материала (преимущества):
- учет психологических особенностей и возможностей младших школьников, а также знаний и умений, с которыми дети пришли в школу.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Вопрос о числе концентров в разное время решался по-разному. В конце 19 в.: 3 конц. 1 дес., 1 сот., многозначные числа. До 1969 г. было 6 концентров: 1) 1-ый десяток; 2) 2-ой десяток; 3) сотня; 4) тысяча; 5) миллион; 6) многозначные числа. Затем по 4-м концентрам. А с 1986 г. в программе 4-хлетней школы – 5 концентров.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Современное построение материала:
десяток

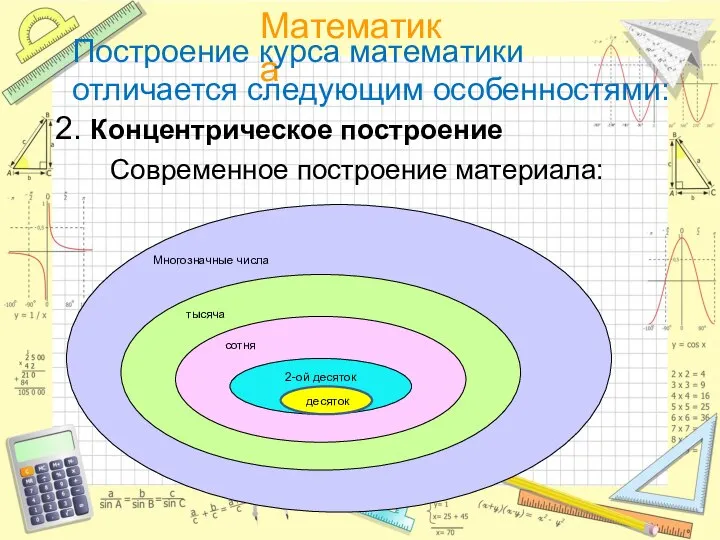
Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Причины выделения концентров
Первый десяток выделен в особый концентр, так как:
каждое число представляет собой совокупность единиц, имеет особое название и изображается особой цифрой;
осуществляется знакомство с действиями сложения и вычитания;
в пределах первого десятка заключается часть таблицы сложения, которую ребенок должен знать на память.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Причины выделения концентров
Второй десяток выделен в особый концентр, так как:
устная нумерация чисел второго десятка имеет свои особенности;
осуществляется знакомство с двузначными числами(образованием, названием, записью);
продолжается знакомство с табличными случаями сложения и вычитания.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Причины выделения концентров
Сотня выделяется, так как:
учащиеся впервые знакомятся с десятичной группой единиц и с вычислительными приемами;
раскрывается сущность десятичной системы счисления;
в этом концентре заключается вся таблица сложения (45 случаев);
впервые дети знакомятся с действиями умножения и деления;
полностью заключена таблица умножения и деления;
впервые учащиеся знакомятся с внетабличным умножением и делением;
впервые дети знакомятся с вычислительными приемами.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Причины выделения концентров
Тысяча выделяется, так как:
в десятичной системе счисления единицы группируются в разряды и классы, все классы построены по образцу класса единиц, нумерация чисел любой величины аналогична нумерации чисел одной тысячи;
на трехзначных числах легче знакомить учащихся с приемами письменных вычислений.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Причины выделения концентров
Многозначные числа выделяются, так как расширяются и обобщаются знания о нумерации и четырех арифметических действиях.

Построение курса математики отличается следующим особенностями:
2. Концентрическое построение
Итак, концентрическое расположение материала – это расположение его по спирали, где на новом витке изучается тот же вопрос, что и ранее, но на более глубоком уровне.

Построение курса математики отличается следующим особенностями:
3. Вопросы теории и вопросы практики органично связаны между собой, сначала изучается правило, а затем вычислительный прием.
4. Сходные или связанные между собой вопросы изучаются в сравнении. + и – изучаются одновременно, также задачи на увеличение и уменьшение. Это дает возможность предотвратить ошибки, выделить существенное, сходное и различное.

Построение курса математики отличается следующим особенностями:
5. Курс математики построен так, что каждое понятие получает свое развитие.
6. Понятия, свойства, закономерности раскрываются в курсе в их взаимосвязи.

Построение курса математики отличается следующим особенностями:
7. Курс строится на системе целесообразно подобранных задач, среди которых большую роль играют текстовые задачи. Они:
являются средством формирования и развития УУД;
являются средством ознакомления с математикой:

Построение курса математики отличается следующим особенностями:
Задачи:
раскрывают смысл арифметических действий;
раскрывают связь между арифметическими действиями;
раскрывают взаимосвязи между компонентами и результатами действий;
помогают формировать геометрические понятия;
раскрывают связь между величинами.
Таким образом, главная роль задач – средство усвоения знаний и развитие ученика.

Спасибо за внимание!