208__155__208__208__186_N_771__134__208__184_N_771__143_1__208__156__208__189__208__190__208__208_N_771__129_N_771__130__208__178__208___208__184__208__190__208__191__208_N_771__128__208_N_771__134__208__18 (1)

План лекции:
Понятие множества
Основные операции над множествами
Числовые множества
Абсолютная величина действительного числа
Понятие функции

Понятие множества
Под множеством понимается совокупность (набор) некоторых объектов. Объекты, которые образуют множество, называются элементами, или точками, этого множества. Если а есть элемент множества А, то используется запись а∈ А. Если b не является элементом множества В, то пишут b ∉ В.
Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ∅.
Если множество В состоит из части элементов множества А или совпадает с ним, то множество В называется подмножеством множества А и обозначается В⊆ А.

Отношения между множествами
Чтобы наглядно изображать множества и отношения между ними, английский математик Дж. Венн предложил
Намного раньше Леонард Эйлер для этих целей использовал круги, при этом точки внутри круга считались элементами множества.
Такие изображения называют диаграммами Эйлера - Венна.

Основные операции
над множествами
Объединением (или суммой) двух множеств A и B называется множество, содержащее все такие и только такие элементы, которые являются элементами хотя бы одного из этих множеств. Объединение множеств A и B обозначают как A ∪ B.
ПРИМЕР.
А={2,4,6,8,10,12,14, 16, 18, 20}
B={4, 7, 10, 13, 16, 19 }
C = A∪B ={2, 4, 6, 7, 8, 10, 12, 13, 14, 16, 18, 19, 20}

Основные операции
над множествами
Пересечением (или умножением) двух множеств A и B называется множество, состоящее из тех и только тех элементов, которые принадлежат множеству A и множеству В одновременно.
Пересечение множеств A и B обозначают как A ∩ B. Например, пересечение четных чисел (множество А) и чисел, делящихся на 3 (множество В), даст множество чисел, делящихся на 6.

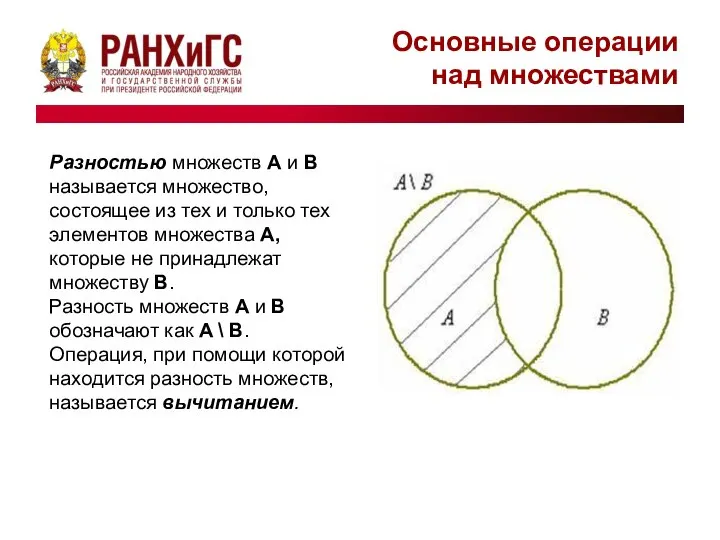
Основные операции
над множествами
Разностью множеств A и B называется множество, состоящее из тех и только тех элементов множества A, которые не принадлежат множеству В.
Разность множеств A и B обозначают как A \ B.
Операция, при помощи которой находится разность множеств, называется вычитанием.

Основные операции
над множествами
Иногда рассматривают симметрическую разность , которая представляет собой объединение
Если В ⊂ А, то разность A \ B называется дополнением множества B до множества A.
Если множество B является подмножеством универсального множества U, то дополнение B до U обозначается ВU , то есть
ВU = U \ B.

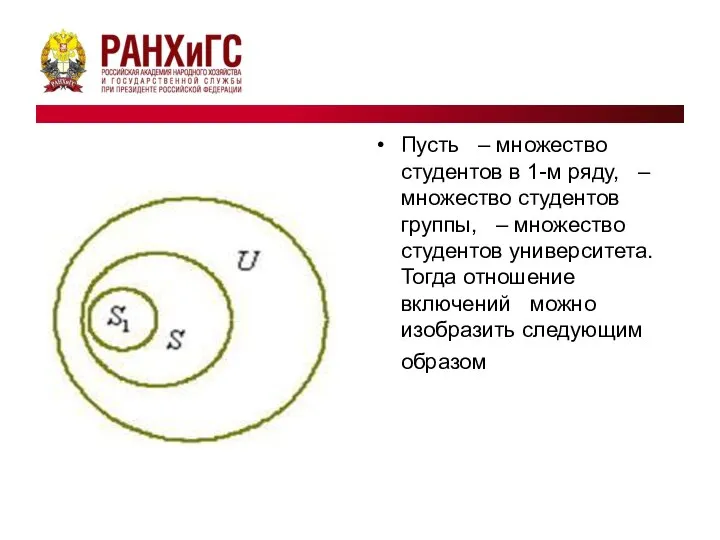
Пусть – множество студентов в 1-м ряду, – множество студентов группы, – множество студентов университета. Тогда отношение включений можно изобразить следующим образом

Декартовым (прямым) произведением множеств А и В называется множество АxВ всех упорядоченных пар
(а, b), в которых элемент а∈ А, а элемент b ∈ В.
Например, декартово произведение множеств

Числовые множества
Множества, элементами которых являются действительные числа, называются числовыми.
Между множеством действительных чисел и точками числовой прямой существует взаимно однозначное соответствие, т.е. каждому действительному числу соответствует определенная точка числовой прямой, и наоборот, каждой точке прямой − определенное действительное число.
Обозначения множеств:
N - множество натуральных чисел
Z- множество целых чисел
R- множество действительных чисел
Q- множество рациональных чисел

Множество может быть упорядоченно по возрастанию ( по убыванию).
Если для множества Х={х} существует такое число М, что для всех x∈ X выполняется условие х ≤ М, то говорят, что множество ограничено числом М сверху. Само число М - в этом случае есть верхняя граница множества Х.
Если для множества Х={х} существует такое число N, что для всех x∈ X выполняется условие х ≥ N, то говорят, что множество ограничено числом N снизу.

Если каждому элементу x из множества X соответствует некоторый элемент y=f(x) из множества Y, то говорят, что задано отображение (соответствие) множества X в множество Y. При этом y называется образом элемента x∈ X , а x– называют прообразом.
Если каждому y∈ Y отвечает в качестве прообраза единственный элемент x∈ X, то отображение называется взаимно однозначным отображением X в Y.
Если между множествами А и В можно установить взаимно однозначное соответствие, то эти множества называются эквивалентными. И обозначаются А ~ В.
Два множества имеют одинаковую мощность, если они эквивалентны друг другу.

Определение метрического
пространства
Множество Е называется метрическим пространством, если каждой паре элементов (х,у) поставлено в соответствие неотрицательное число ρ(х,у) (расстояние между х и у) , удовлетворяющее следующим условиям:
ρ(х,у)=0 только тогда, когда х=у. (аксиома тождества);
ρ(х,у)= ρ(у,х) (аксиома симметрии);
ρ(х,у)≤ ρ(х,z)+ ρ(z,у) для любых х,у и z из Е (аксиома треугольника).

n-мерное Евклидово пространство
Пусть Еn – множество всевозможных упорядоченных последовательностей из n действительных чисел х(х1,х2,…хn), у(у1,у2,…уn), z(z1,z2,..zn).
х,у,z – называют точками, а последовательности из n действительных чисел х1,х2,…хn; у1,у2,…уn; z1,z2,..zn – называют координатами точки.
Множество Еn называется n-мерным евклидовым пространством, если в нем введено понятие расстояния, определяемое по формуле: