Абсолютные и относительные величины

Абсолютные величины используются при характеристике общей совокупности
(численность населения, общее число врачей в стране и др.), а также при оценке редко встречающихся явлений (число особо опасных инфекций, число людей с аномалиями развития).

Производные величины подразделяются на относительные и средние.
Относительные величины используются при анализе альтернативных (есть явление или отсутствует) признаков.

Виды относительных величин:
1) экстенсивные коэффициенты;
2) интенсивные коэффициенты;
3) коэффициенты соотношения;
4) коэффициенты наглядности.

Экстенсивные коэффициенты характеризуют отношение части к целому, то есть определяют долю (удельный вес), процент части в целом, принятом за 100%. Используются для характеристики структуры статистической совокупности.
Например: удельный вес (доля) заболеваний гриппом среди всех заболеваний в процентах; доля производственных травм среди всех травм у рабочих (отношение числа производственных травм к общему числу травм, умноженное на 100%).

Интенсивные коэффициенты отражают частоту (уровень распространенности) явления в своей среде. На практике их применяют для оценки здоровья населения, медико-демографических процессов.
Например: число случаев заболеваний с временной утратой трудоспособности на 100 работающих; число заболевших гипертонической болезнью на 100 жителей; число родившихся на 1000 человек (определяется как отношение числа родившихся за год к средней численности населения административной территории, умноженное на 1000).

Интенсивные коэффициенты бывают общие и специальные.
Общие: показатель рождаемости, общий показатель заболеваемости и др.;
Специальные (характеризуются более узким основанием): число женщин детородного возраста (плодовитость), число женщин, заболевших гипертонической болезнью, и др..

Коэффициенты соотношения характеризуют отношение двух самостоятельных совокупностей. Используются для характеристики обеспеченности (уровня и качества) медицинской помощью: число коек на 10000 человек; число врачей на 10000 жителей; число прививок на 1000 жителей (отношение числа лиц, охваченных прививками, к численности населения административной территории, умноженное на 1000).

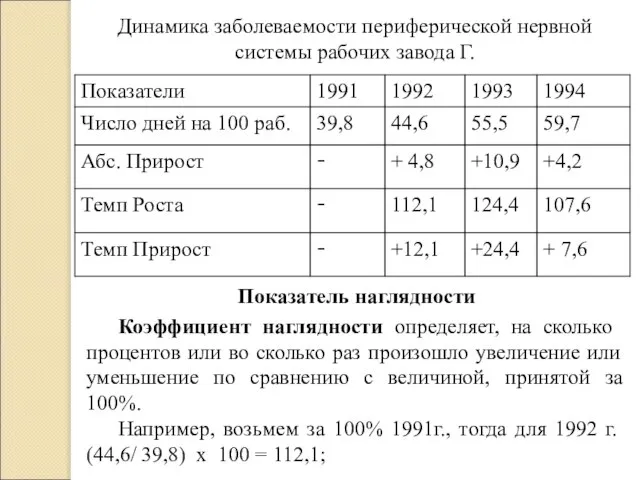
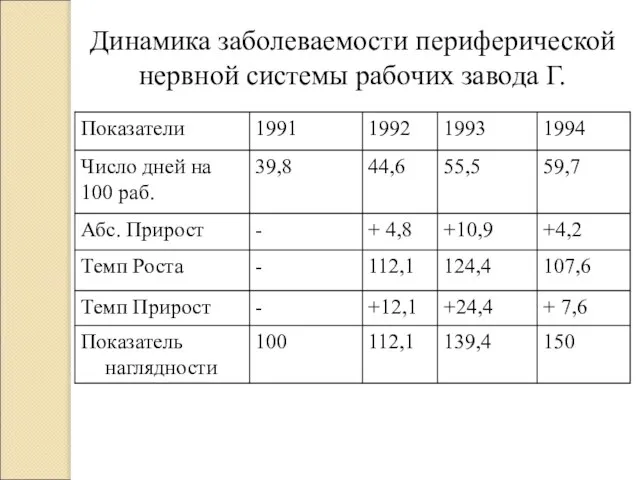
Коэффициент наглядности определяет, на сколько процентов или во сколько раз произошло увеличение или уменьшение по сравнению с величиной, принятой за 100%. Используется для характеристики динамики явления. Например, число врачей в 1995 г. по сравнению с числом врачей в 1994 г., принятым за 100% (отношение числа специалистов в данном году к числу специалистов в предыдущем году, умноженное на 100%).

Динамические ряды
Одной из важнейших задач медицины и здравоохранения является изучение здоровья населения, а также деятельности лечебно-профилактических
учреждений в динамике.
Для изучения динамики того или иного-процесса необходимо уметь сопоставить динамические ряды разных типов, уметь их выравнивать и анализировать.

Динамический ряд — это ряд однородных статистических величин, показывающих изменение явления во времени.
Числа, из которых состоит динамический ряд, называются уровнями ряда.

Простой динамический ряд
Ряд, построенный из абсолютных величин, называется простым.
Обычно он выражает численность населения в различные годы или периоды; количество медицинских учреждений, больничных коек, врачей, санитарных обследований и т.д..

Производный (сложный) динамический ряд:
Средними величинами (среднее число лабораторных анализов за неделю).
Относительными показателями (изменение рождаемости, заболеваемости, травматизма, обеспеченности врачами).

Моментный динамический ряд – характеризует явление на определенный момент времени (на конец года, месяца, декады и т.д.).
Интервальный ряд – состоит из величин, которые характеризуют явление за определенный промежуток времени (за год, за месяц и т.п.).
Интервальный ряд в отличие от моментного можно разделить на более дробный период, а также можно укрупнить интервалы.
Все относительные числа, характеризующие здоровье населения, а также показатели деятельности медицинских учреждений, как правило, представлены в виде интервальных рядов.

Анализ скорости и интенсивности развития явления во времени осуществляется с помощью статистических показателей, которые получаются в результате сравнения уровней между собой.
К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста. При этом принято сравниваемый уровень называть отчётным, а уровень, с которым производят сравнение, — базисным.

Абсолютный прирост
Абсолютный прирост характеризует размер увеличение (уменьшения) уровня ряда за определенный период времени.
Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста.
Абсолютный прирост представляет собой разность между последующим и предыдущим уровнем.

Темп роста
Показатель интенсивности изменения уровня ряда в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или темпом роста.
Коэффициент роста и темп роста представляют собой две формы выражения интенсивности изменения уровня. Коэффициент роста показывает, во сколько раз данный уровень ряда больше базисного уровня или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени.
Темп роста — это отношение последующего уровня к предыдущему, умноженное на 100%.

Темп прироста
Темп прироста характеризует относительную скорость изменения уровня ряда в единицу времени.
Темп прироста показывает, на какую долю (или процент) уровень данного периода или момента времени больше (или меньше) базисного уровня.
Темп прироста является отношением абсолютного прироста (снижения) к предыдущему уровню, умноженным на 100%.

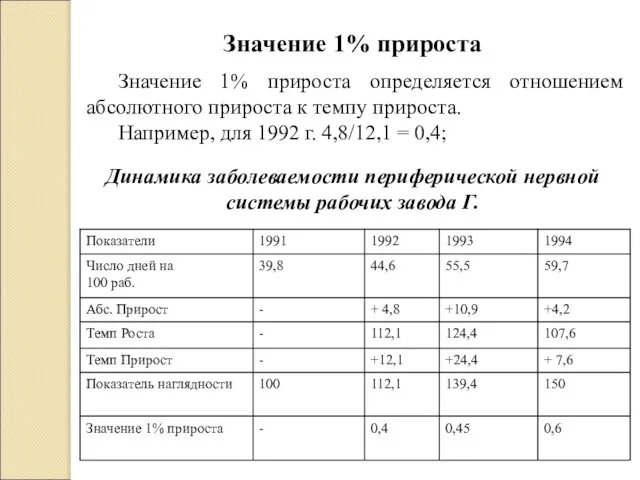
Значение 1% прироста
В статистической практике часто вместо расчета и анализа темпов роста и прироста рассматривают абсолютное значение одного процента прироста.
Оно представляет собой одну сотую часть базисного уровня и в то же время — отношение абсолютного прироста к соответствующему темпу прироста. Абсолютное значение одного процента прироста служит косвенной мерой базисного уровня и вместе с темпом прироста позволяет рассчитать абсолютный прирост уровня за рассматриваемый период.
Значение 1% прироста определяется отношением абсолютного прироста к темпу прироста.

Методы выравнивания ряда:
Метод укрупнения интервалов. Если рассматривать уровни экономических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдаются снижение и повышение этих уровней.
Метод простой скользящей средней. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней, затем — средний уровень такого же числа уровней, начиная со второго, далее — начиная с третьего и т. д. Т.о. при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Отсюда название — скользящая средняя.

Каждое звено скользящей средней — это средний уровень за соответствующий период, который относится к середине выбранного периода. Для каждого конкретного ряда динамики алгоритм расчета скользящей средней следующий:
Определить интервал сглаживания, то есть число входящих в него уровней m (m
Вычислить среднее значение уровней, образующих интервал сглаживания, которое одновременно является сглаживающим значением уровня, находящегося в центре интервала сглаживания, при условии, что m — нечетное число.
Сдвинуть интервал сглаживания на одну точку вправо, потом вычислить по формуле сглаженное значение для t+1 члена, снова произвести сдвиг и т. д..

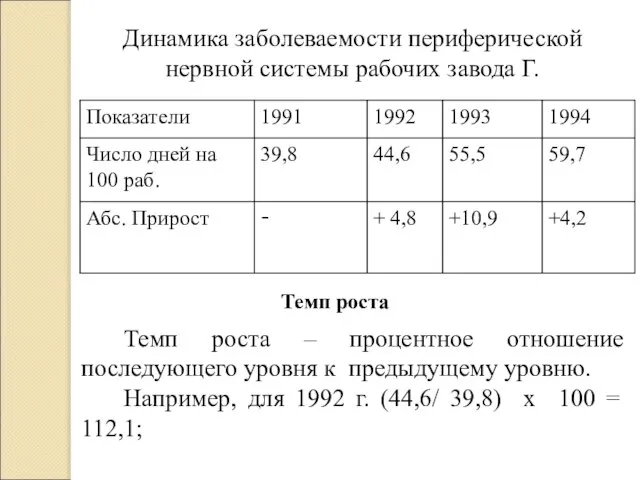
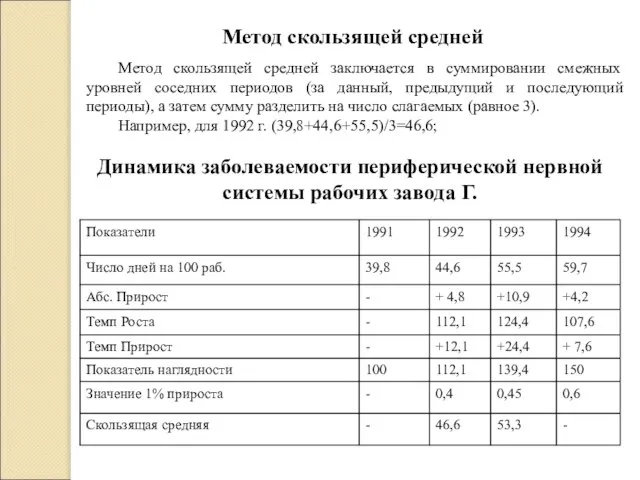
Динамика заболеваемости периферической нервной системы рабочих завода Г.
Абсолютный прирост
Абсолютный прирост – разность уровня данного года и предыдущего
Например, для 1992 г. – 44,6 – 39,8 = 4,8

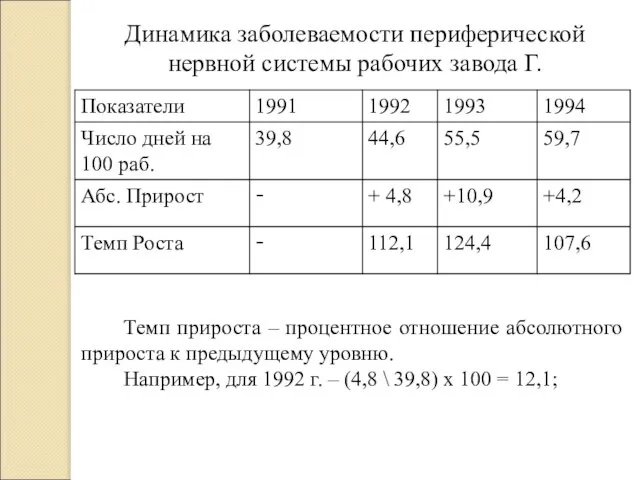
Динамика заболеваемости периферической нервной системы рабочих завода Г.
Темп роста
Темп роста – процентное отношение последующего уровня к предыдущему уровню.
Например, для 1992 г. (44,6/ 39,8) х 100 = 112,1;

Динамика заболеваемости периферической нервной системы рабочих завода Г.
Темп прироста – процентное отношение абсолютного прироста к предыдущему уровню.
Например, для 1992 г. – (4,8 \ 39,8) х 100 = 12,1;

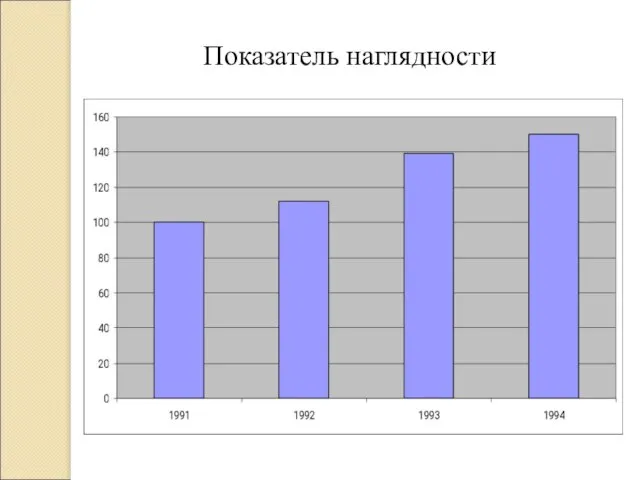
Динамика заболеваемости периферической нервной системы рабочих завода Г.
Показатель наглядности
Коэффициент наглядности определяет, на сколько процентов или во сколько раз произошло увеличение или уменьшение по сравнению с величиной, принятой за 100%.
Например, возьмем за 100% 1991г., тогда для 1992 г. (44,6/ 39,8) х 100 = 112,1;

Динамика заболеваемости периферической нервной системы рабочих завода Г.

Показатель наглядности

Значение 1% прироста
Значение 1% прироста определяется отношением абсолютного прироста к темпу прироста.
Например, для 1992 г. 4,8/12,1 = 0,4;
Динамика заболеваемости периферической нервной системы рабочих завода Г.

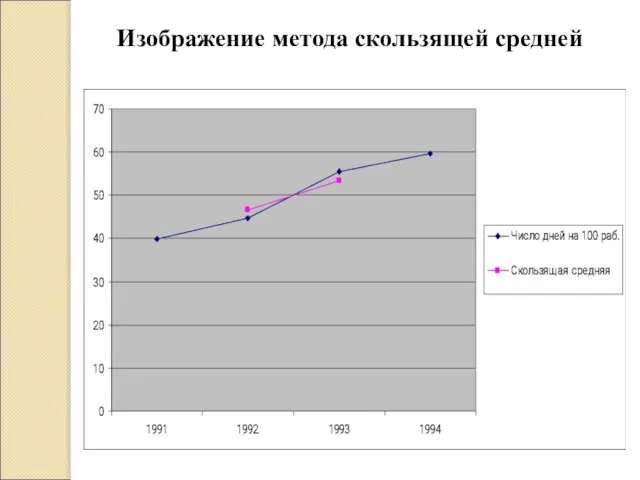
Метод скользящей средней
Метод скользящей средней заключается в суммировании смежных уровней соседних периодов (за данный, предыдущий и последующий периоды), а затем сумму разделить на число слагаемых (равное 3).
Например, для 1992 г. (39,8+44,6+55,5)/3=46,6;
Динамика заболеваемости периферической нервной системы рабочих завода Г.

Изображение метода скользящей средней

Использование метода стандартизации при оценке здоровья населения и показателей работы учреждений здравоохранения: Метод стандартизации используется при оценке показателей здоровья только при сравнении их уровней. Этот метод расчета условных величин применяется для устранения неоднородности состава сравниваемых коллективов. Он показывает, какой был бы уровень заболеваемости (травматизма, смертности, инвалидизации и др.) в каждом коллективе (учреждении, городе), если бы его состав (по возрасту, по полу, по стажу и др.) был одинаков.

Стандартизованные показатели используют при необходимости сравнения уровней смертности (заболеваемости) от злокачественных заболеваний (болезней органов пищеварения и т. д.) в разных городах, районных центрах; сравнения уровней заболеваемости (травматизма) на разных производствах; сравнения уровней летальности в разных больницах (отделениях).
Метод позволяет установить причину (пол, возраст, состав по тяжести заболевания) разных уровней заболеваемости или медико-социальные и гигиенические характеристики (влияние факторов риска, условий труда, образа жизни, факторов окружающей среды и др.).