Содержание
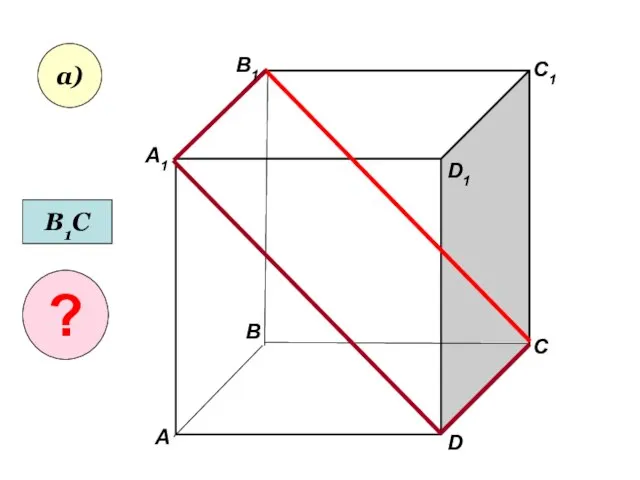
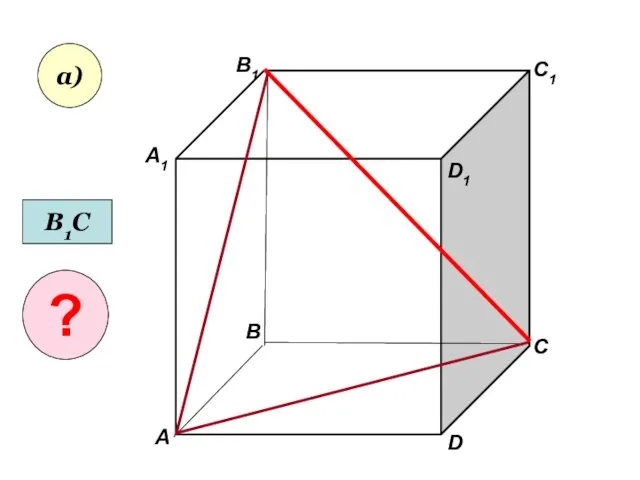
- 2. А А1 В В1 С D1 D C1 а) В1С ?
- 3. А А1 В В1 С D1 D C1 а) В1С ?
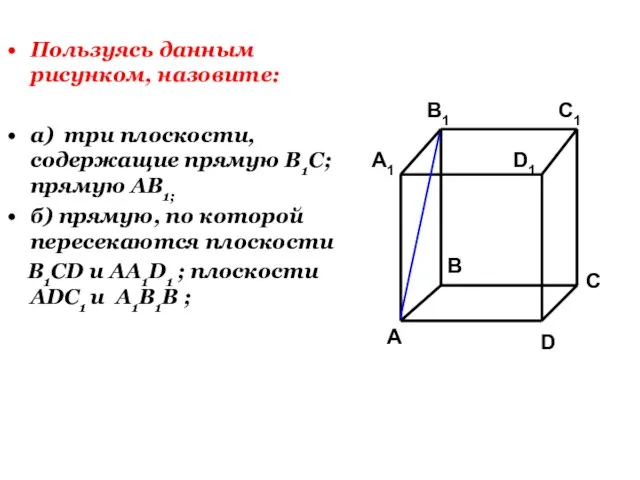
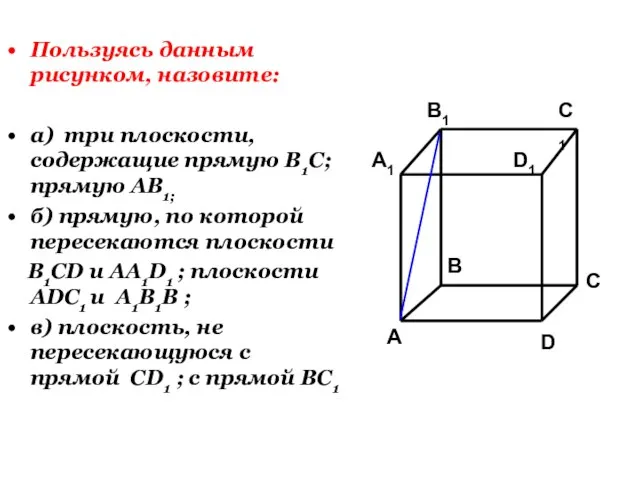
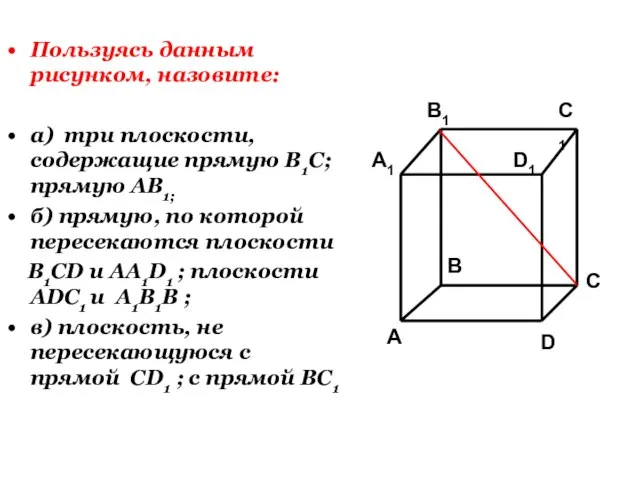
- 4. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
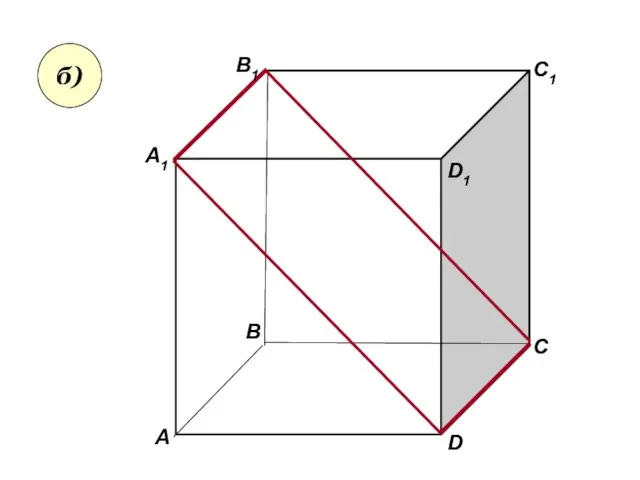
- 5. А А1 В В1 С D1 D C1 б)
- 6. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
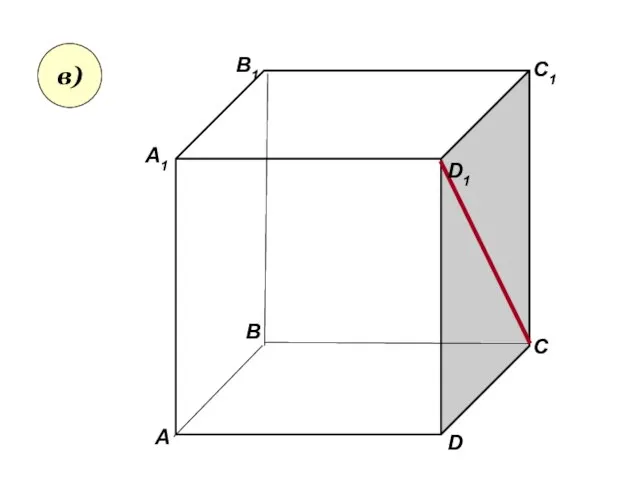
- 7. А А1 В В1 С D1 D C1 в)
- 8. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
- 9. Решение задач на применение аксиом стереометрии и их следствий. МОУ СОШ № 256 г.Фокино № 2
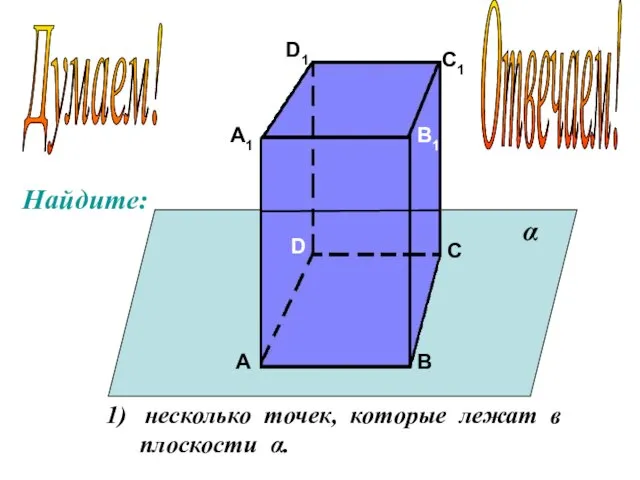
- 10. А А1 В В1 С С1 D D1 несколько точек, которые лежат в плоскости α. α
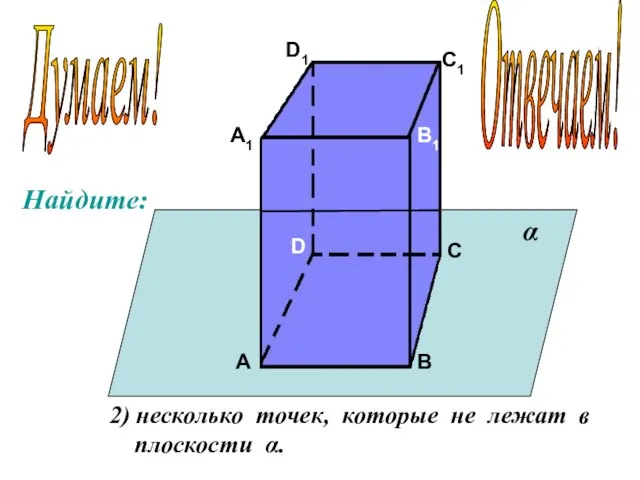
- 11. А А1 В В1 С С1 D D1 2) несколько точек, которые не лежат в плоскости
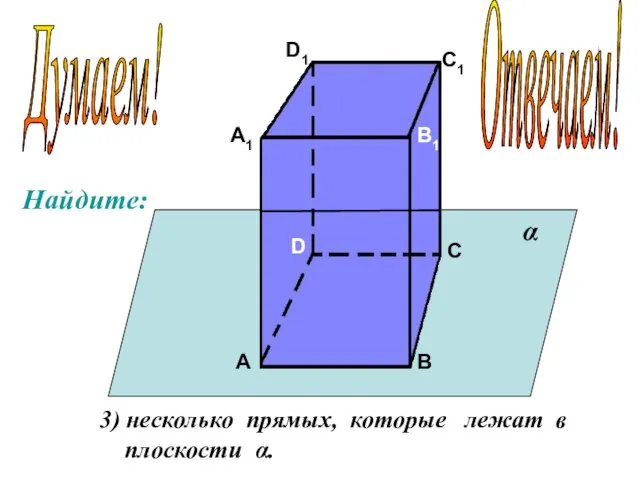
- 12. А А1 В В1 С С1 D D1 3) несколько прямых, которые лежат в плоскости α.
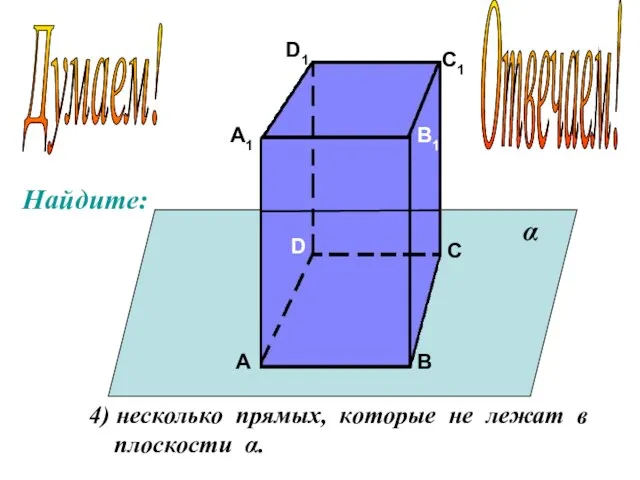
- 13. А А1 В В1 С С1 D D1 4) несколько прямых, которые не лежат в плоскости
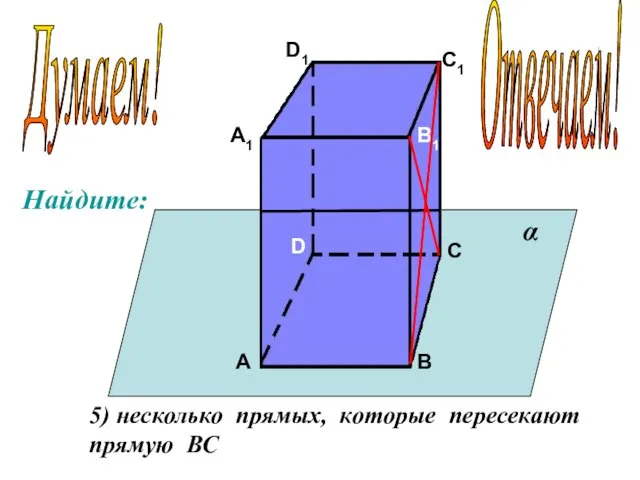
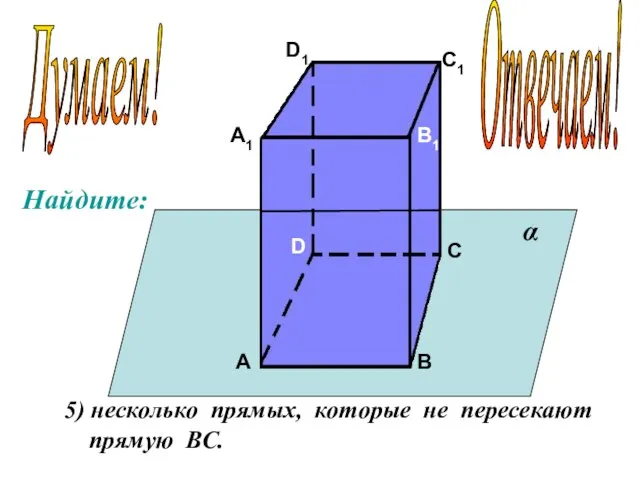
- 14. А А1 В В1 С С1 D D1 5) несколько прямых, которые пересекают прямую ВС α
- 15. А А1 В В1 С С1 D D1 5) несколько прямых, которые не пересекают прямую ВС.
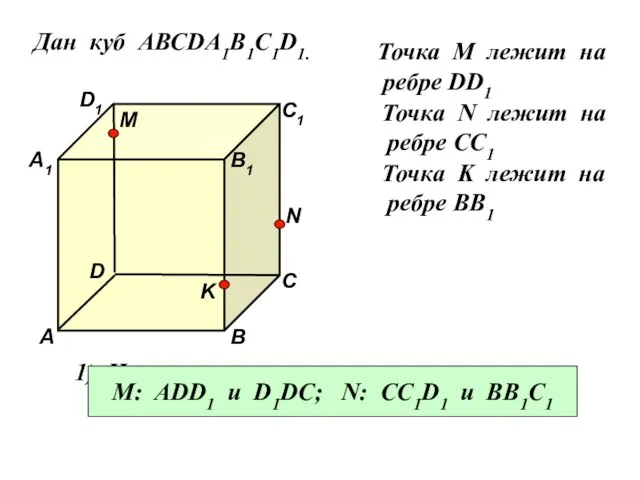
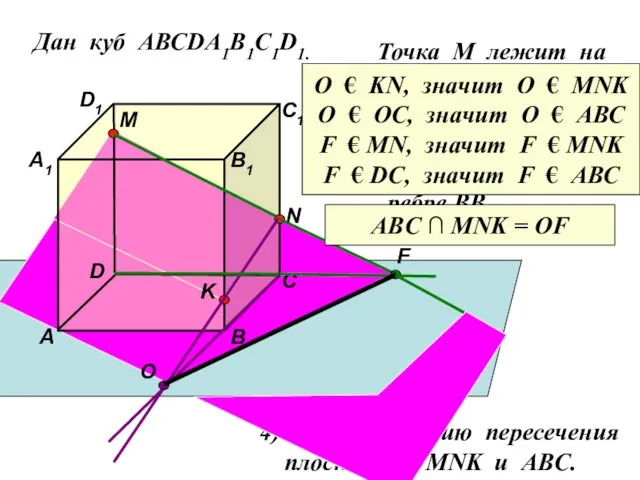
- 16. Дан куб АВСDA1B1C1D1. Точка М лежит на ребре DD1 Точка N лежит на ребре CC1 Точка
- 17. Дан куб АВСDA1B1C1D1. D1 D С1 С В1 В А1 А M Точка М лежит на
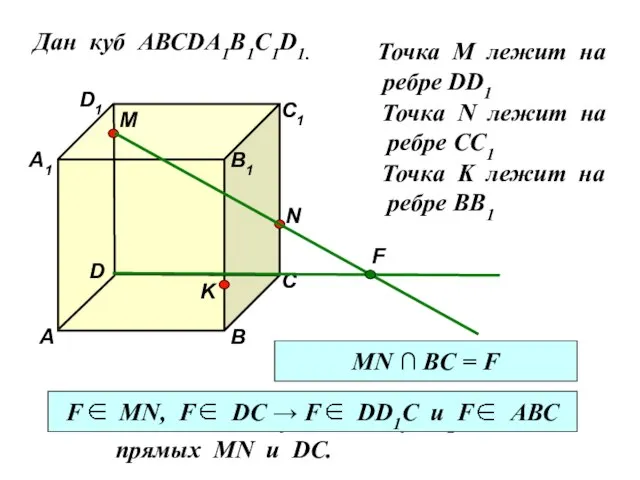
- 18. Дан куб АВСDA1B1C1D1. D1 D С1 С В1 В А1 А M Точка М лежит на
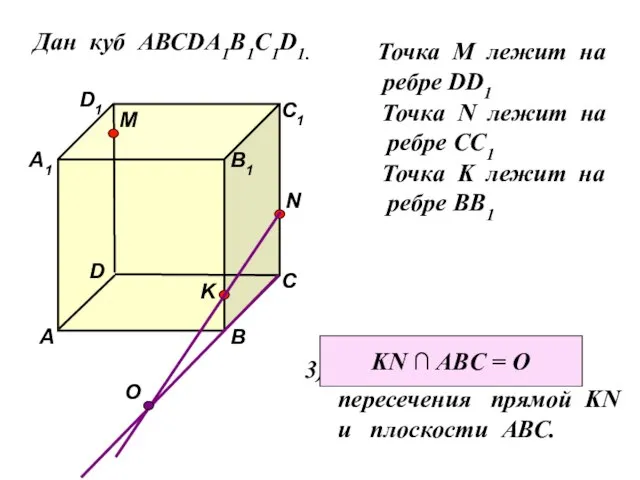
- 19. Дан куб АВСDA1B1C1D1. D1 D С1 С В1 В А1 А M Точка М лежит на
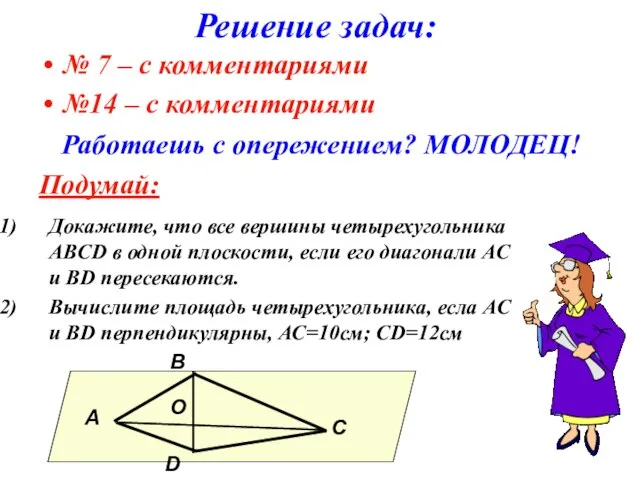
- 20. Решение задач: № 7 – с комментариями №14 – с комментариями Работаешь с опережением? МОЛОДЕЦ! Подумай:
- 21. Домашнее задание: Повторить теоретический материал пп 1 - 3 №№ 9; 11; 13; 15 В рабочей
- 23. Скачать презентацию


 Первый питательный крем от Anew - Ультра-Питание
Первый питательный крем от Anew - Ультра-Питание American Society Demographics
American Society Demographics  Презентация на тему Бородинская битва 4 класс
Презентация на тему Бородинская битва 4 класс Девиантное поведение
Девиантное поведение КУЛЬТУРА РОССИИ XIV — XVI ВЕКА
КУЛЬТУРА РОССИИ XIV — XVI ВЕКА Дефекты в кристаллах
Дефекты в кристаллах «Разработка Единой медицинской информационной системы на платформе 1С:Предприятие»
«Разработка Единой медицинской информационной системы на платформе 1С:Предприятие» Разработка и вывод на рынок аппарата плазменной коагуляции, на основе низкотемпературной плазмы
Разработка и вывод на рынок аппарата плазменной коагуляции, на основе низкотемпературной плазмы Презентация на тему Модест Петрович Мусоргский
Презентация на тему Модест Петрович Мусоргский Компьютерные вирусы
Компьютерные вирусы Дополнительные цвета
Дополнительные цвета Конституция Российской Федерации: государственные символы России
Конституция Российской Федерации: государственные символы России урок 15_ — копия _2_
урок 15_ — копия _2_ В землянке
В землянке Самсон
Самсон Моя наука
Моя наука Назарларыңызға әлемдегі 10 сәнді банкноттар жайлы
Назарларыңызға әлемдегі 10 сәнді банкноттар жайлы Французское искусство XVII века
Французское искусство XVII века Презентация на тему кпд тепловых двигателей 8 класс
Презентация на тему кпд тепловых двигателей 8 класс  Организационно-правовые основы деятельности первичной профсоюзной организации
Организационно-правовые основы деятельности первичной профсоюзной организации Кошки и собаки
Кошки и собаки Эффективное обшение
Эффективное обшение Права ребенка
Права ребенка Презентация на тему Природное и культурное наследие России
Презентация на тему Природное и культурное наследие России  Между парадигмами. Особенности исследования того, что еще не стало мейнстримом
Между парадигмами. Особенности исследования того, что еще не стало мейнстримом Культурология как наука
Культурология как наука Что изучает ФИЗИКА ?
Что изучает ФИЗИКА ? Звукопоглощающие материалы и конструкции
Звукопоглощающие материалы и конструкции