Слайд 2В этом году мы изучали степенные функции у = хn c натуральным

показателем.
Но первое знакомство с такими функциями произошло еще в 7 классе. Это функции у = х2 и у = х3.
Я решила сделать презентацию «Функция у = х3» для объяснения этой темы учащимся 7 класса.
Слайд 4ЦЕЛЬ
ИЗУЧИТЬ СВОЙСТВА И ГРАФИК ДАННОЙ ФУНКЦИИ,
НАУЧИТЬСЯ НАХОДИТЬ ЗНАЧЕНИЕ ФУНКЦИИИ,
ЗНАЧЕНИЕ

АРГУМЕНТА ПО ГРАФИКУ,
СТРОИТЬ ГРАФИК ФУНКЦИИ.
Слайд 5КАКИЕ ИЗ ТОЧЕК НЕ ПРИНАДЛЕЖАТ ГРАФИКУ ФУНКЦИИ У=Х2 ?
ОПРЕДЕЛИТЕ БЕЗ ВЫЧИСЛЕНИЙ.
А(-1;1)

М(-2;-4) К(0;8)
В(3;-9) Х(1,5;2,25) Д(16;0)
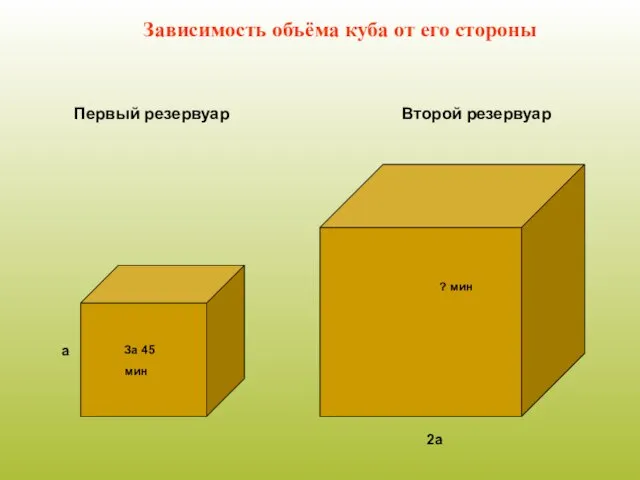
Слайд 6Объем куба V=a3
a = 1 V=?
a = 2 V=?
a = 3 V=?
a

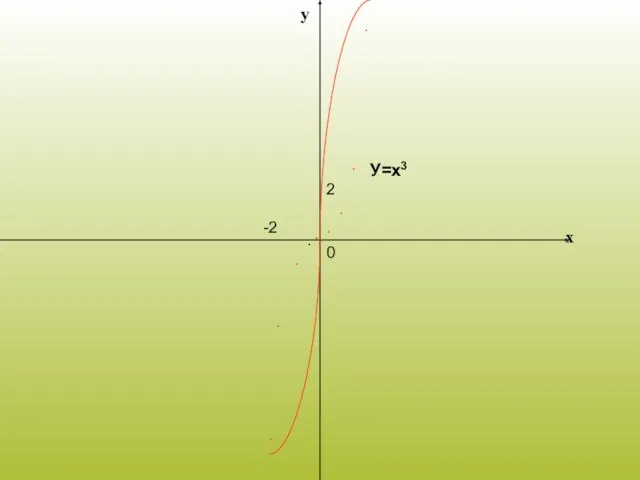
Слайд 7у = х3
Этапы построения графика функции

Слайд 9Свойства функции у = х3
Область определения: х - любое число.
Если х =

0, то у = 0. График функции проходит через начало координат.
Если х > 0, то у > 0, если
х< 0, то у < 0. График расположен в 1 и 3 координатных четвертях.
Противоположным значениям х соответствуют противоположные значения у.
Слайд 10За 45 мин
а
2а
? мин
Первый резервуар
Второй резервуар
Зависимость объёма куба от его стороны








 Тема урока:Прикладная среда графического редактора Paint.
Тема урока:Прикладная среда графического редактора Paint. Презентация на тему Система национальных счетов
Презентация на тему Система национальных счетов Двадцатилетний брак великого князя Московского Василия III с Соломонией Сабуровой был бесплоден. Отправив законную жену в монастыр
Двадцатилетний брак великого князя Московского Василия III с Соломонией Сабуровой был бесплоден. Отправив законную жену в монастыр Cn(H2O)m
Cn(H2O)m 20140111_prezentatsiya_k_igre
20140111_prezentatsiya_k_igre Умей предупреждать болезни
Умей предупреждать болезни Еженедельное совещание. Статус работ блока Геология и разработка
Еженедельное совещание. Статус работ блока Геология и разработка Изделие Святой Николаус-Чудотворец
Изделие Святой Николаус-Чудотворец Среднее арифметическое, мода и размах ряда.
Среднее арифметическое, мода и размах ряда. Амплуа игроков в волейболе и их функции
Амплуа игроков в волейболе и их функции Страховые представители АО Страховая компания СОГАЗ-Мед
Страховые представители АО Страховая компания СОГАЗ-Мед «EVA 2011 Москва» 28 – 30 ноября 2011 Сбор и долговременное сохранение электронной информации в сфере культуры. Л.А. Куйбышев, Н.В. Браккер,
«EVA 2011 Москва» 28 – 30 ноября 2011 Сбор и долговременное сохранение электронной информации в сфере культуры. Л.А. Куйбышев, Н.В. Браккер,  Диего Веласкес. Сдача Бреды 1634–1635
Диего Веласкес. Сдача Бреды 1634–1635 К НЕМУ НЕ ЗАРАСТЕТНАРОДНАЯ ТРОПА А. С. Пушкину посвящается…
К НЕМУ НЕ ЗАРАСТЕТНАРОДНАЯ ТРОПА А. С. Пушкину посвящается… тема: «Воображение как общая способность»
тема: «Воображение как общая способность»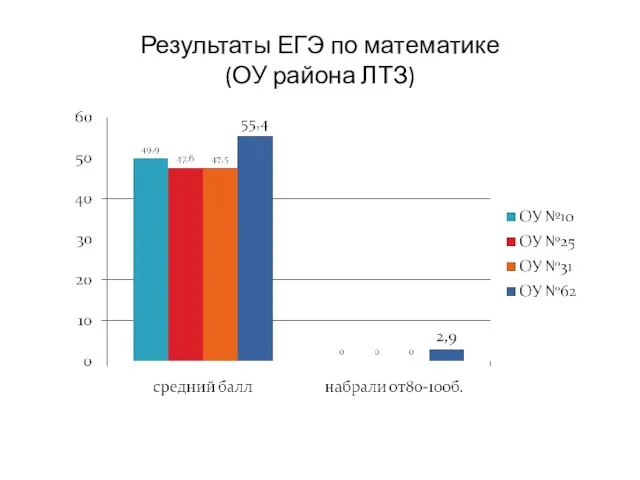 Результаты ЕГЭ по математике (ОУ района ЛТЗ)
Результаты ЕГЭ по математике (ОУ района ЛТЗ) Качество влияния личности на ход истории (на примере А. Гитлера и И. Сталина)
Качество влияния личности на ход истории (на примере А. Гитлера и И. Сталина) Организация обучения учителей по курсу «Основы религиозных культур и светской этики» в Калининградской области
Организация обучения учителей по курсу «Основы религиозных культур и светской этики» в Калининградской области ООО Глобал Контейнер Лоджистикс
ООО Глобал Контейнер Лоджистикс Жак Рене Ширак
Жак Рене Ширак Игра в слова
Игра в слова Бизнес-план Пончиковой
Бизнес-план Пончиковой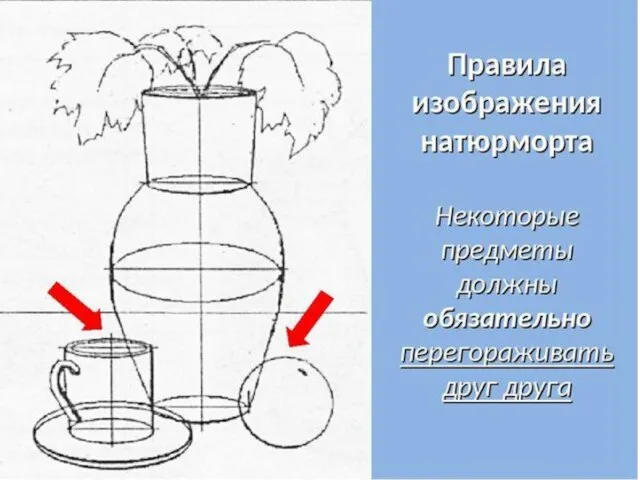 Занятие 3 года обучения на каникулах. Декоративный натюрморт
Занятие 3 года обучения на каникулах. Декоративный натюрморт Лабораторная группаРезультаты серологического этапа ДЭН выводы, задачи2008 год
Лабораторная группаРезультаты серологического этапа ДЭН выводы, задачи2008 год Виды наказаний
Виды наказаний Ультразвуковой датчик
Ультразвуковой датчик Легенды театральной сцены
Легенды театральной сцены ПОДПИСКА
ПОДПИСКА