Содержание
- 2. О практиках Работа в группах из 3-х человек. Постарайтесь сформировать группы, в которых будет хотя бы
- 3. Практика №1 «Программирование рекурсивных процедур и функций»
- 4. Основная задача Понять и реализовать 3 различных алгоритма нахождения чисел Фибоначчи. Подсказка: один алгоритм рекурсивный, два
- 5. Задача повышенной сложности Рекурсивно вычислить определитель матрицы разложением по строке/столбцу. Возможно ли вычислить итерационно? 03.10.2022 НИУ
- 6. Практика №2 «Продолжение работы с рекурсивными и итерационными алгоритмами»
- 7. Задача с прошлого занятия Рекурсивно вычислить определитель матрицы разложением по строке/столбцу. Возможно ли вычислить итерационно? 03.10.2022
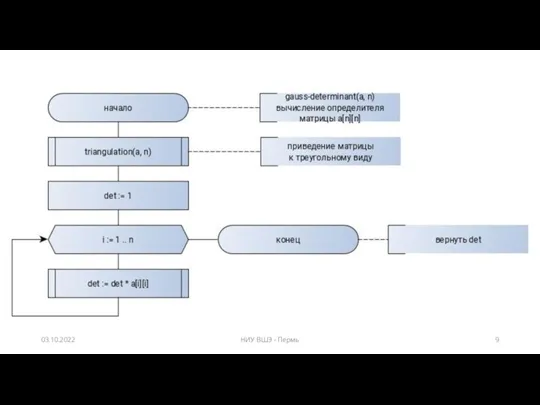
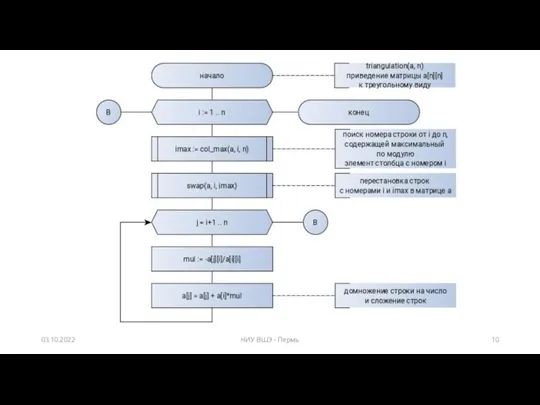
- 8. Задача на определитель матрицы Вычислить рекурсивно определитель матрицы с помощью метода Гаусса. Какой метод более точный
- 9. 03.10.2022 НИУ ВШЭ - Пермь
- 10. 03.10.2022 НИУ ВШЭ - Пермь
- 11. Практика №3 «Рекуррентные соотношения и итерационный алгоритм»
- 12. Задача по генерации перестановок Рекурсивная генерация всех n-факториал перестановок. Параметр n задаётся от 0 до 9.
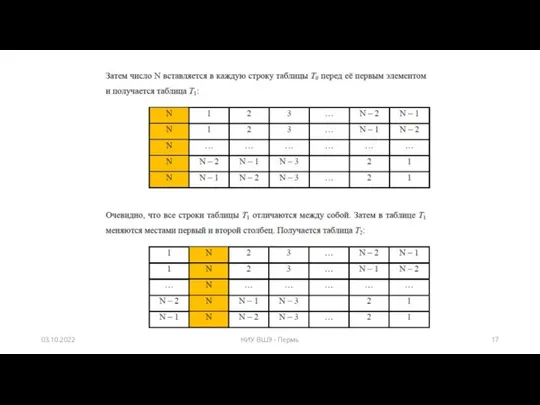
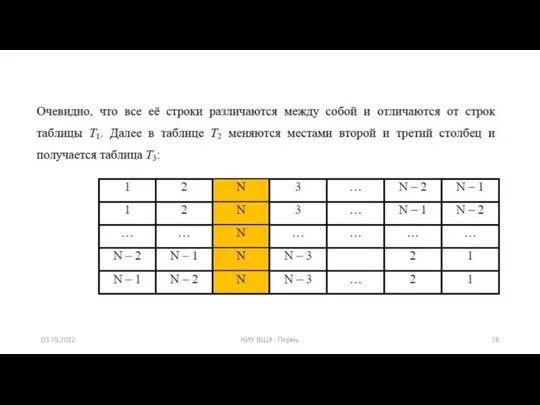
- 13. Задача по генерации перестановок Например, найти все возможные перестановки для последовательности чисел 1, 2, 3. Существуют
- 14. Задача по генерации перестановок Дополнительно дублирую слайды с лекции: 03.10.2022 НИУ ВШЭ - Пермь
- 15. 03.10.2022 НИУ ВШЭ - Пермь
- 16. 03.10.2022 НИУ ВШЭ - Пермь
- 17. 03.10.2022 НИУ ВШЭ - Пермь
- 18. 03.10.2022 НИУ ВШЭ - Пермь
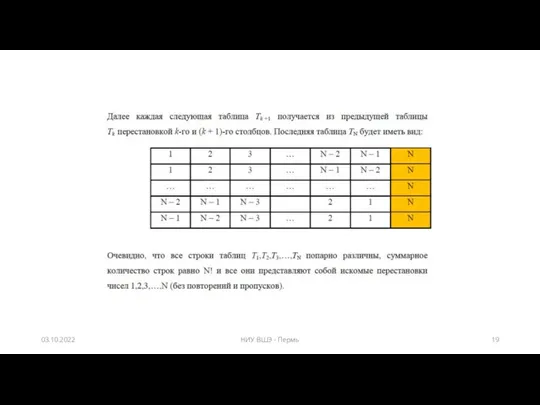
- 19. 03.10.2022 НИУ ВШЭ - Пермь
- 20. Задача по вычислению ленточного определителя Вычисление ленточного определителя (из презентации с лекции): итерационный способ; на основе
- 21. 03.10.2022 НИУ ВШЭ - Пермь
- 22. 03.10.2022 НИУ ВШЭ - Пермь
- 23. 03.10.2022 НИУ ВШЭ - Пермь
- 24. 03.10.2022 НИУ ВШЭ - Пермь
- 25. Практика №4 «Рекурсивное (по двум параметрам) и итерационное вычисление НОД и НОК (быстрый и медленный алгоритм
- 26. Задача по вычислению НОД и НОК Вычислить НОД (англ. greatest common divisor) и НОК (англ. least
- 27. Задача по вычислению НОД и НОК Где каждое последующее число является остатком от деления предпредыдущего на
- 28. Задача по вычислению НОД и НОК Дополнительно можете доказать описанное ранее утверждение, а также попробуйте реализовать
- 29. Практика №5 «Взаимная и двойная рекурсия»
- 30. Задача по взаимной рекурсии Необходимо сгенерировать все строки длины n в алфавите {0, 1}, в которых
- 31. Задача по двойной рекурсии 03.10.2022 НИУ ВШЭ - Пермь
- 32. Задача по двойной рекурсии (продолжение) 03.10.2022 НИУ ВШЭ - Пермь
- 34. Скачать презентацию


























 Философский мистицизм XX века
Философский мистицизм XX века Символические образы в романе И.А. Гончарова «Обломов»
Символические образы в романе И.А. Гончарова «Обломов» «Современный урок- как основа эффективного и качественного образования» Подготовила: Е.П. Абаева, заместитель директора по УВР
«Современный урок- как основа эффективного и качественного образования» Подготовила: Е.П. Абаева, заместитель директора по УВР ПРЕДПРИЯТИЯ СТАВРОПОЛЬСКОГО КРАЯ
ПРЕДПРИЯТИЯ СТАВРОПОЛЬСКОГО КРАЯ Чистота–залог здоровья
Чистота–залог здоровья Композиция - важнейший организующий компонент художественной формы
Композиция - важнейший организующий компонент художественной формы Строение сложноподчинённых предложений
Строение сложноподчинённых предложений Безопасность дорожного движения 2006-2010
Безопасность дорожного движения 2006-2010 Тема 12 Прикладной уровень сети Internet Презентацию лекций разработал доцент кафедры оптимизации систем управления Томского полите
Тема 12 Прикладной уровень сети Internet Презентацию лекций разработал доцент кафедры оптимизации систем управления Томского полите Глобальная сеть Internet Word Wide Web
Глобальная сеть Internet Word Wide Web Презентация на тему Сравнительное наблюдение за прорастанием семян
Презентация на тему Сравнительное наблюдение за прорастанием семян ОРГАНИЗАЦИЯ И ПРОВЕДЕНИЕ УСТНОЙ И ПИСЬМЕННОЙ ЧАСТИ ЭКЗАМЕНА ПО АНГЛИЙСКОМУ ЯЗЫКУ ГОСУДАРСТВЕННОЙ ИТОГОВОЙ АТТЕСТАЦИИ ОБУЧАЮЩИХС
ОРГАНИЗАЦИЯ И ПРОВЕДЕНИЕ УСТНОЙ И ПИСЬМЕННОЙ ЧАСТИ ЭКЗАМЕНА ПО АНГЛИЙСКОМУ ЯЗЫКУ ГОСУДАРСТВЕННОЙ ИТОГОВОЙ АТТЕСТАЦИИ ОБУЧАЮЩИХС Наши права и обязанности (8 класс)
Наши права и обязанности (8 класс) Урок математики с Машей и Мишей
Урок математики с Машей и Мишей Ханс Христиан Андерсен «Принцесса на горошине»
Ханс Христиан Андерсен «Принцесса на горошине» Кроссворд Виды спорта
Кроссворд Виды спорта Число Авогадро
Число Авогадро Презентация на тему Белый медведь
Презентация на тему Белый медведь Важность инновационных продуктов в создании стоимости и качества активов в аптечном секторе
Важность инновационных продуктов в создании стоимости и качества активов в аптечном секторе Методическое объединение учителей начальных классов
Методическое объединение учителей начальных классов Почему донорство полезно?
Почему донорство полезно? Сечение. 8 класс
Сечение. 8 класс Платежные системы
Платежные системы Электронный ридер Plastic Logic
Электронный ридер Plastic Logic Презентация на тему Разложение многочленов на множители
Презентация на тему Разложение многочленов на множители  Вокально-интонационные упражнения на уроках младшего хора
Вокально-интонационные упражнения на уроках младшего хора Личностно – ориентированный подход в обучении химии
Личностно – ориентированный подход в обучении химии Всемирная акция «Голубь мира»
Всемирная акция «Голубь мира»