Содержание
- 2. Содержание Повторение основных понятий теории графов Понятие остовного связного дерева Понятие цикломатического числа Алгоритм Прима Алгоритм
- 3. Основные понятия теории графов По горизонтали: г р а ф 9. Наглядное сред-ство представления состава и
- 4. Основные понятия теории графов По вертикали: г р а ф р е б р о п
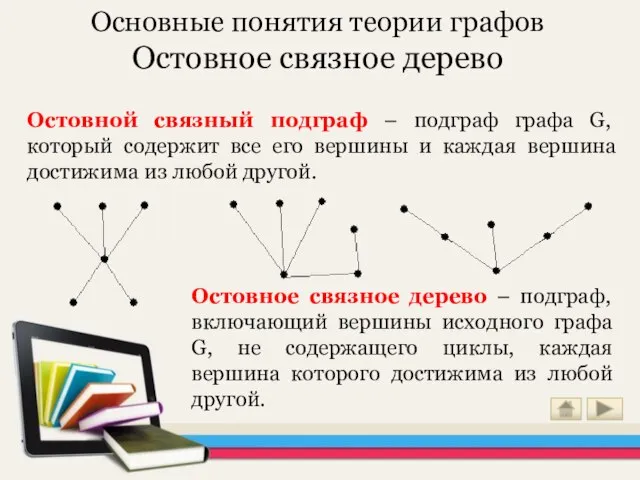
- 5. Основные понятия теории графов Остовное связное дерево Остовной связный подграф – подграф графа G, который содержит
- 6. Цикломатическое число γ показывает, сколько ребер нужно удалить из графа, чтобы в нем не осталось циклов
- 7. Задача 1 В некотором районе было решено провести газопровод между пятью деревнями. От Кошкино до Мышкино
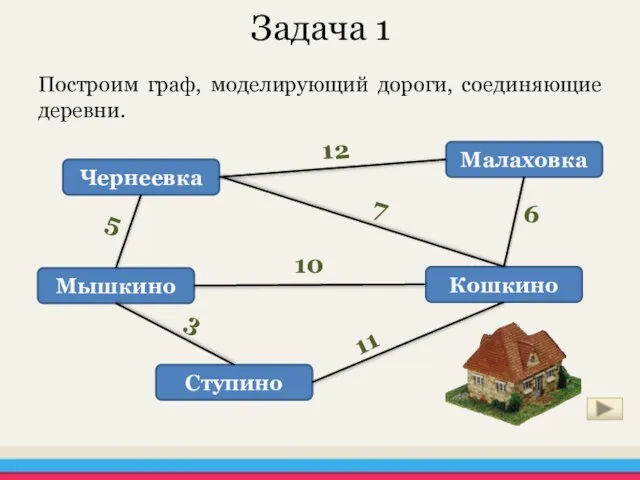
- 8. Задача 1 Построим граф, моделирующий дороги, соединяющие деревни.
- 9. Задача 1 Задача сводится к построению остовного связного дерева минимального веса. Рассчитаем цикломатическое число. m (количество
- 10. Алгоритм Прима Пусть дан взвешенный неориентированный граф. Для построения минимального остовного дерева необходимо: 1. Представить граф
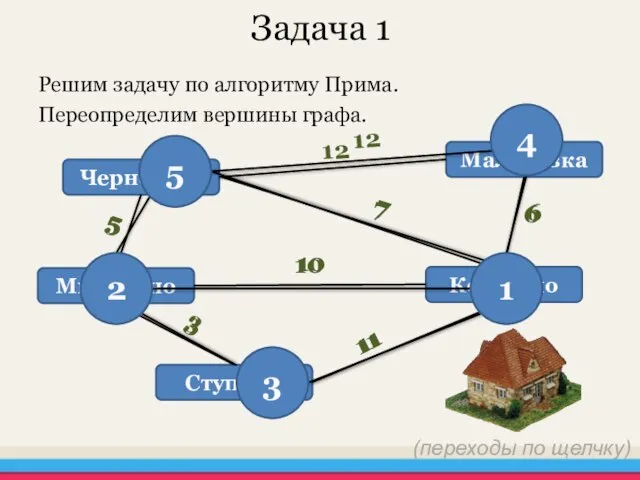
- 11. Задача 1 Решим задачу по алгоритму Прима. Переопределим вершины графа. (переходы по щелчку)
- 12. Задача 1 Представим граф в виде матрицы смежности. Найдем минимальный элемент. Он равен 3 3 3
- 13. Задача 1 Вычеркнем 2-ю и 3-ю строки таблицы. А столбцы 2 и 3 выделим. Найдем минимальный
- 14. Задача 1 Вычеркнем 5-ю строку таблицы. А столбец 5 выделим. Найдем минимальный элемент в выделенных столбцах.
- 15. Задача 1 Вычеркнем 1-ю строку таблицы. А столбец 1 выделим. Найдем минимальный элемент в выделенных столбцах.
- 16. Задача 1 Вычеркнем 4-ю строку таблицы. А столбец 4 выделим. (переходы по щелчку)
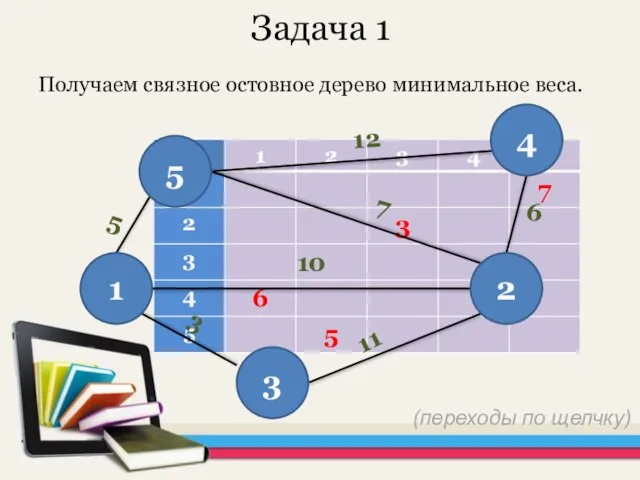
- 17. Задача 1 Получаем связное остовное дерево минимальное веса. 12 7 10 11 3 6 5 5
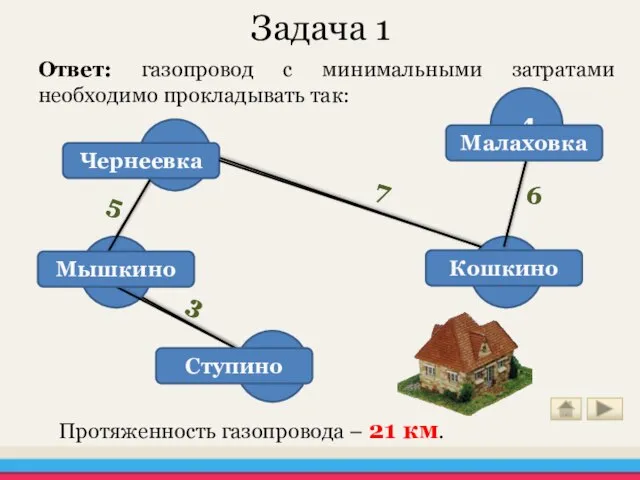
- 18. Задача 1 Ответ: газопровод с минимальными затратами необходимо прокладывать так: Протяженность газопровода – 21 км.
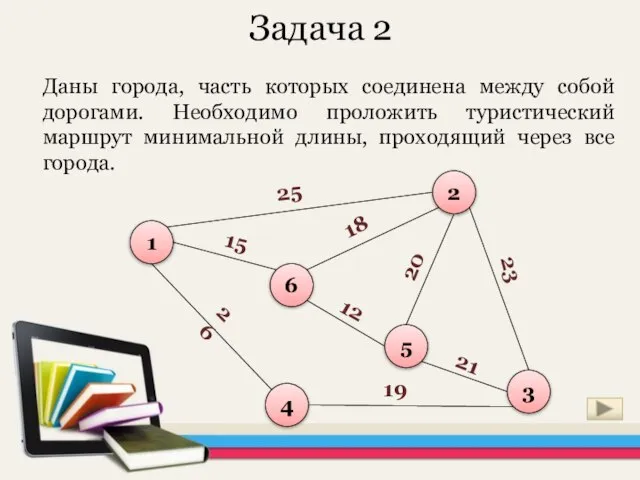
- 19. Задача 2 Даны города, часть которых соединена между собой дорогами. Необходимо проложить туристический маршрут минимальной длины,
- 20. Задача 2 Задача сводится к построению остовного связного дерева минимального веса. Рассчитаем цикломатическое число. m (количество
- 21. Алгоритм Крускала Удалить все ребра и получить остовной подграф с изолированными вершинами. Отсортировать ребра по возрастанию.
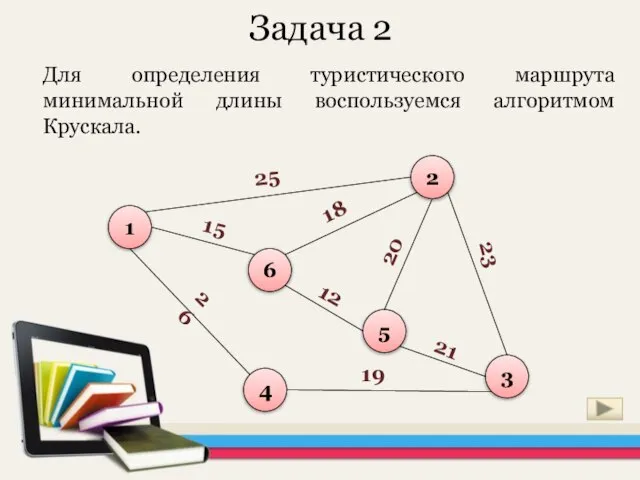
- 22. Задача 2 Для определения туристического маршрута минимальной длины воспользуемся алгоритмом Крускала.
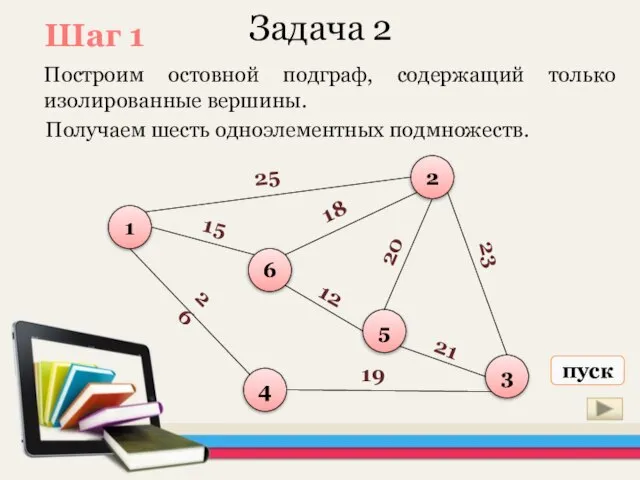
- 23. Задача 2 Построим остовной подграф, содержащий только изолированные вершины. 1 6 5 2 3 4 25
- 24. Задача 2 Найдем ребро минимального веса и добавим его в остовной подграф. 1 6 5 2
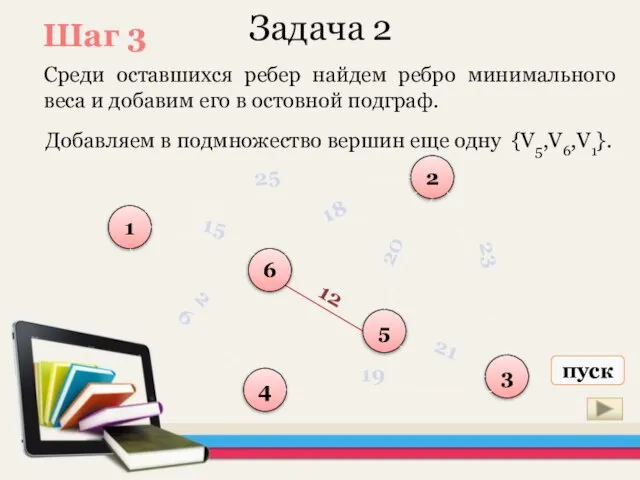
- 25. Задача 2 Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф. 1
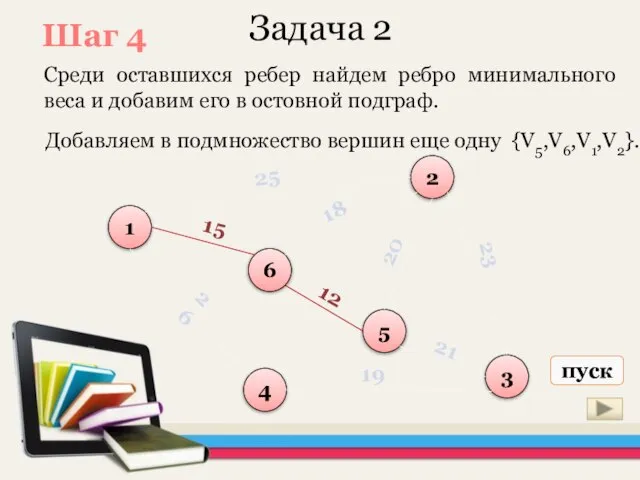
- 26. Задача 2 Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф. 1
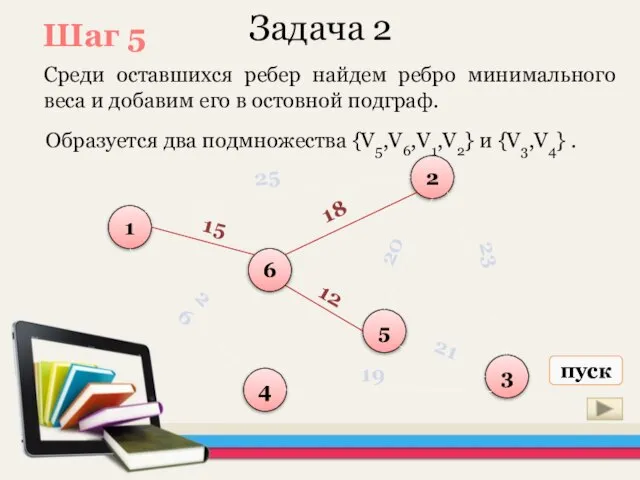
- 27. Задача 2 Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф. 1
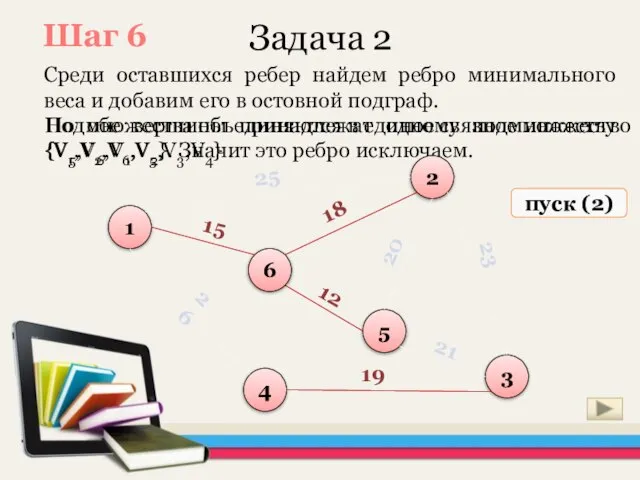
- 28. Но обе вершины принадлежат одному подмножеству {V5,V6,V1,V2}. Значит это ребро исключаем. Задача 2 Среди оставшихся ребер
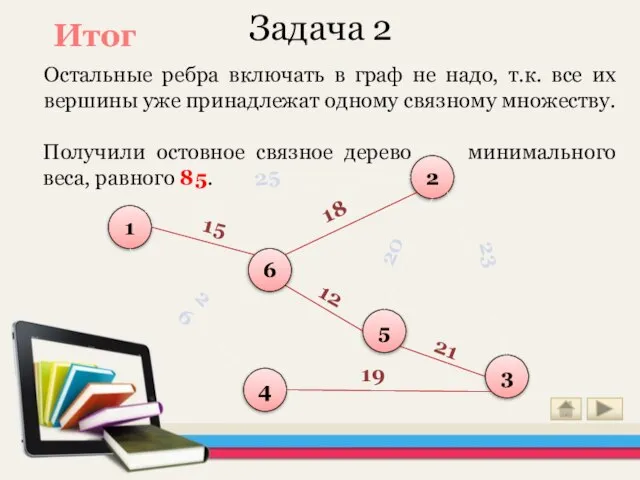
- 29. Задача 2 Остальные ребра включать в граф не надо, т.к. все их вершины уже принадлежат одному
- 30. Вопросы Построенный граф (в задачах 1 и 2) является Почему? В граф включены все вершины Все
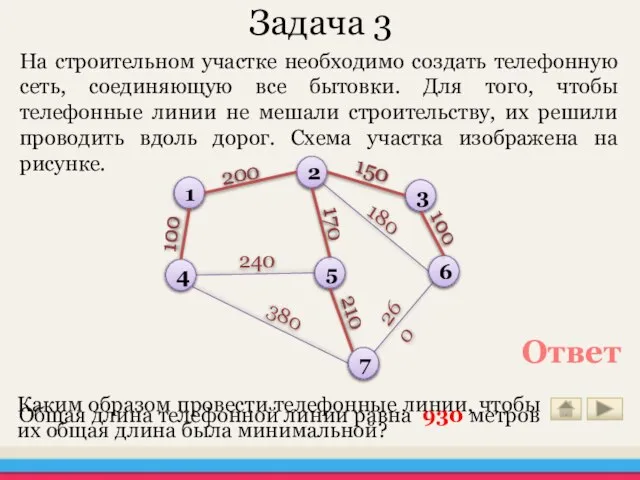
- 31. Задача 3 На строительном участке необходимо создать телефонную сеть, соединяющую все бытовки. Для того, чтобы телефонные
- 32. Источники Кроссворд создан на сайте и расположен по адресу http://puzzlecup.com/?guess=3C2D4A01E0522AAU Информатика и ИКТ. Профильный уровень: учебник
- 34. Скачать презентацию

















 Особенности истории России. Место России в мировом историческом процессе
Особенности истории России. Место России в мировом историческом процессе Оппортунистические инфекции
Оппортунистические инфекции  Всемирный день борьбы со СПИДом
Всемирный день борьбы со СПИДом Доказательная медицина и стандарты медицинской деятельности
Доказательная медицина и стандарты медицинской деятельности Система счетов и двойная запись
Система счетов и двойная запись Презентация на тему Лепка из пластилина
Презентация на тему Лепка из пластилина  Ночевала тучка золотая
Ночевала тучка золотая Revision
Revision Материально-производственная деятельность человека.
Материально-производственная деятельность человека. Как помочь ребёнку быть внимательным.
Как помочь ребёнку быть внимательным. Защитники земли русской. Работы учеников
Защитники земли русской. Работы учеников Презентация на тему ПОЛИТИЧЕСКИЙ ПРОГНОЗ: сущность, научные основы и принципы
Презентация на тему ПОЛИТИЧЕСКИЙ ПРОГНОЗ: сущность, научные основы и принципы  Словообразование (6 класс)
Словообразование (6 класс) 1 сентября. Классный час «От пера до компьютера».
1 сентября. Классный час «От пера до компьютера». Грамматические особенности перевода арабских фильмов на русский язык
Грамматические особенности перевода арабских фильмов на русский язык 1.3.2 Логические элементы ЭВМ
1.3.2 Логические элементы ЭВМ HTML
HTML Психологический климат в трудовом коллективе
Психологический климат в трудовом коллективе НОУ СОШ Гармония
НОУ СОШ Гармония Китайско-конфуцианская цивилизация
Китайско-конфуцианская цивилизация Каракули. Упражнение 2
Каракули. Упражнение 2 Презентация на тему Треугольники 7 класс геометрия
Презентация на тему Треугольники 7 класс геометрия  Moral Crisis in south Africa
Moral Crisis in south Africa Промоагентство
Промоагентство Презентация на тему Проблема темперамента и характера
Презентация на тему Проблема темперамента и характера Мой творческий путь в прозе и стихах
Мой творческий путь в прозе и стихах ПРОГРАММА«ТРИ ШАГА К УНИКАЛЬНОМУ СЕРВИСУ»GLOBAL SOLUTIONS Ltd.
ПРОГРАММА«ТРИ ШАГА К УНИКАЛЬНОМУ СЕРВИСУ»GLOBAL SOLUTIONS Ltd. Политические режимы. Типы политических режимов
Политические режимы. Типы политических режимов