Алгоритмы топологической оптимизации транспортных сетей

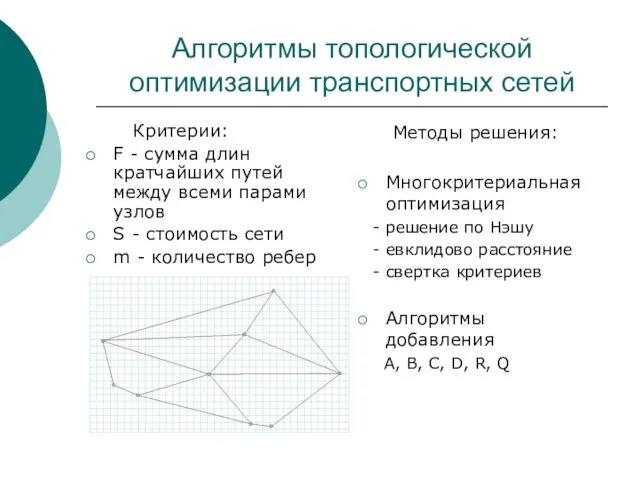
Алгоритмы топологической оптимизации транспортных сетей
Критерии:
F - сумма длин кратчайших путей между всеми парами узлов
S - стоимость сети
m - количество ребер
Методы решения:
Многокритериальная оптимизация
- решение по Нэшу
- евклидово расстояние
- свертка критериев
Алгоритмы добавления
A, B, C, D, R, Q

Решение по Нэшу
Минимизация функции
E=(F-F*)(S-S*)
F* - значение критерия F на полном графе
S* - стоимость минимального связывающего дерева
Удаляем ребро, при удалении которого максимально уменьшается значение критерия E

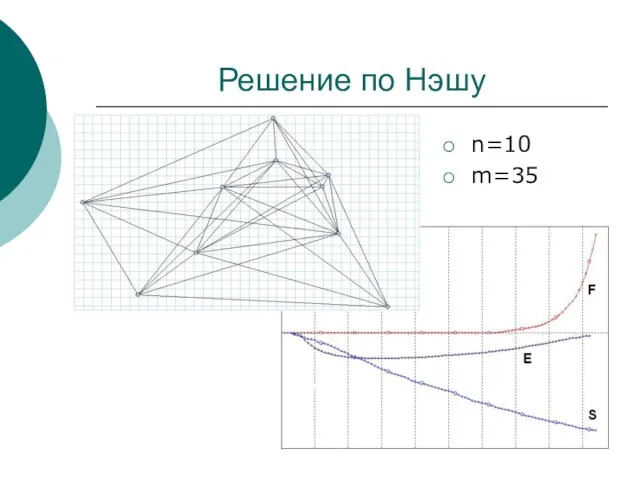
Решение по Нэшу
n=10
m=35

Метод идеальной точки
Минимизация функции
(F*, S*) – «идеальная точка»
(F, S) – точка-текущие значения критериев
Удаляем ребро, при удалении которого максимально уменьшается расстояние до идеальной точки

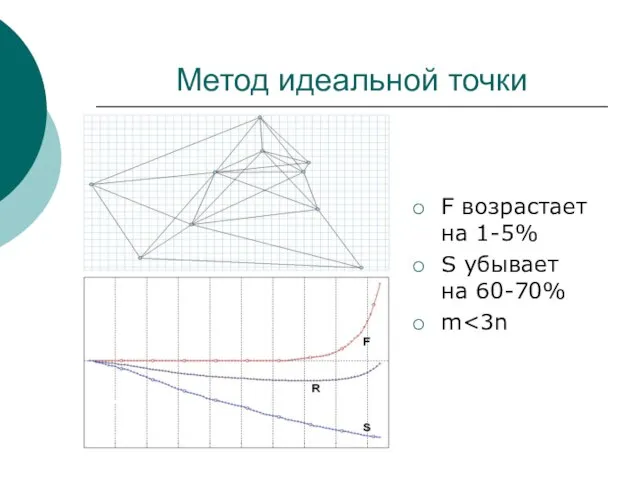
Метод идеальной точки
F возрастает
на 1-5%
S убывает
на 60-70%
m<3n

Свертка критериев
Минимизация функции
Удаляем ребро, при удалении которого максимально уменьшается значение критерия Q
Изменение изменяет положение минимума Q

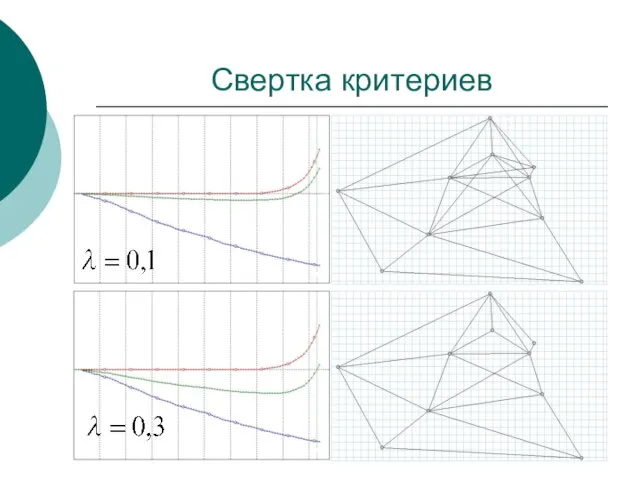
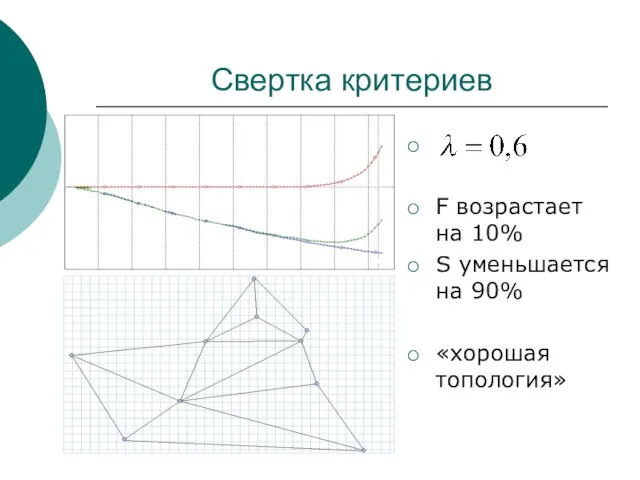
Свертка критериев

Свертка критериев
F возрастает
на 10%
S уменьшается
на 90%
«хорошая топология»

Алгоритмы добавления
А. Добавляем самое короткое ребро.
В. Добавляем ребро, при добавлении которого приращение F будет максимально.
C. Добавляем ребро, при добавлении которого отношение будет максимально.
D. Добавляем ребро, которое максимально уменьшается значение критерия E.
R. Добавляем ребро, которое максимально уменьшает расстояния до (F*, S*).
Q. Добавляем ребро, которое максимально уменьшается значение критерия Q.