Анализ измерений

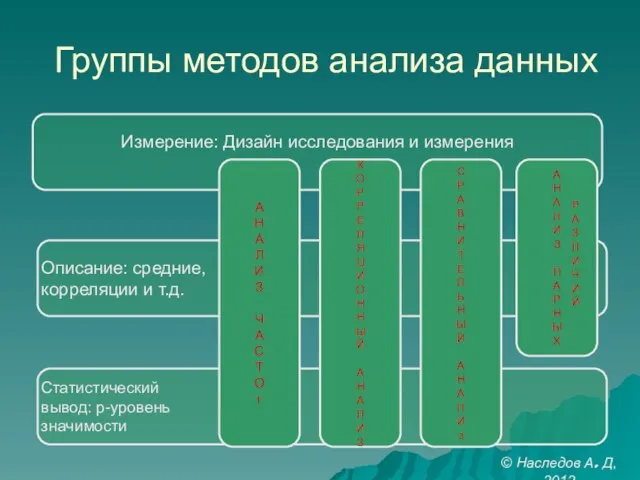
Группы методов анализа данных
Р
А
З
Л
И
Ч
И
Й
© Наследов А. Д, 2012

Номинальные измерения:
анализ частот
Распределение (критерии согласия)
Таблица сопряженности
Анализ соответствий
Логлинейный анализ таблиц сопряженности
© Наследов А. Д, 2012

Содержательная гипотеза: связь X и Y.
Измерения: X и Y номинальные переменные
Анализ классификации: сравнение эмпирического и теоретического (ожидаемого) распределений
Примеры: 1) Кто чаще обращается в службу знакомств: мужчины или женщины? 2) Зависит ли посещаемость занятий от дня недели? 3) Предпочитаются ли некоторые хобби чаще, чем другие?
Анализ таблиц сопряженности: связь двух оснований классификации
Примеры: 1) Отличаются ли юноши и девушки по предпочитаемым хобби? 2) Зависит ли предпочтение одного из пяти кандидатов на выборах от пола избирателя (от его района проживания и т.п.). 3) Повлияло ли суггестивное воздействие на предпочтение одной из двух альтернатив?
© Наследов А. Д, 2012

Сравнение эмпирического бинарного и теоретического распределений (2-х долей): критерий согласия
χ2 (Хи-квадрат, Chi-Square) и биномиальный критерий (с. 125)
Р – число ячеек
с эмпирическими частотами
А если при том же соотношении N = 100?
© Наследов А. Д, 2012

Критерий согласия Хи-квадрат:
более 2-х градаций (с. 129)
© Наследов А. Д, 2012

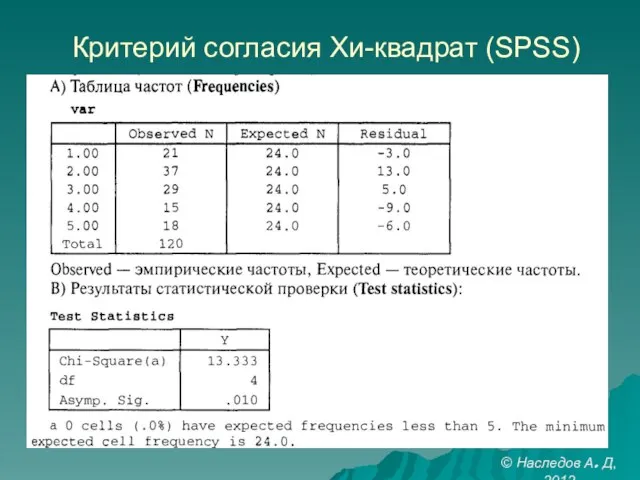
Критерий согласия Хи-квадрат (SPSS)
© Наследов А. Д, 2012

Таблицы сопряженности (с. 132)
© Наследов А. Д, 2012

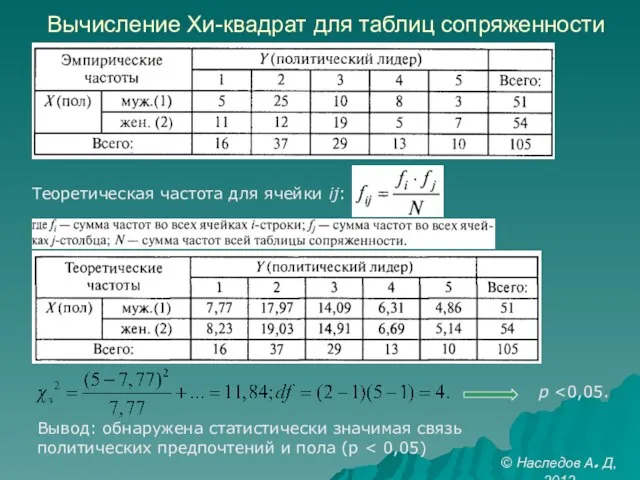
Вычисление Хи-квадрат для таблиц сопряженности
Теоретическая частота для ячейки ij:
p <0,05.
Вывод: обнаружена статистически значимая связь
политических предпочтений и пола (p < 0,05)
© Наследов А. Д, 2012

Таблицы сопряженности 2х2 (с. 135)
© Наследов А. Д, 2012

Таблица 2х2: независимые выборки (с. 136)
ВАЖНО: ДАННЫЕ ПРЕДСТАВЛЯЮТ СОБОЙ ДВЕ ПЕРЕМЕННЫЕ!
Критерий Хи-квадрат с поправкой на непрерывность:
Теоретические частоты:
Альтернатива: 2-сторонняя или 1-сторонняя?
Допускается 1-сторонняя
альтернатива!
© Наследов А. Д, 2012

Таблицы 2х2: повторные измерения бинарной переменной (с. 139)
Критерий Хи-квадрат не применим!
Критерий Мак-Нимара:
p - ?
© Наследов А. Д, 2012

Сравнительный анализ
Методы сравнения двух выборок
Однофакторный ANOVA и непараметрические аналоги
Многофакторный ANOVA
Многомерный ANOVA
Дискриминантный анализ
ANOVA с повторными измерениями
© Наследов А. Д, 2012

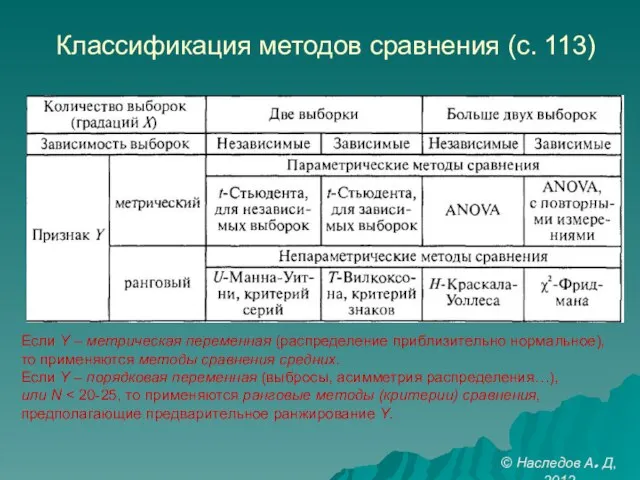
Классификация методов сравнения (с. 113)
Если Y – метрическая переменная (распределение приблизительно нормальное),
то применяются методы сравнения средних.
Если Y – порядковая переменная (выбросы, асимметрия распределения…),
или N < 20-25, то применяются ранговые методы (критерии) сравнения,
предполагающие предварительное ранжирование Y.
© Наследов А. Д, 2012

Разработал Р.Фишер (1920-е гг.) – для анализа экспериментальных данных
Основные понятия:
Фактор (X - независимая переменная) – группирующая, номинальная, характеризуется уровнями (градациями).
Уровень = группа (выборка).
Зависимая переменная – (Y) – метрическая.
Т.о. каждому уровню фактора соответствует среднее значение зависимой переменной.
Межгрупповые факторы – уровням соответствуют независимые выборки.
Внутригрупповые факторы – уровням соответствуют зависимые выборки.
Фиксированные и случайные факторы.
Ковариата – метрическая независимая переменная, «включаемая» в анализ наряду с фактором.
© Наследов А. Д, 2012

Принципиальная идея ANOVA
В дисперсии зависимой переменной выделяется две составляющие:
межгрупповая (Df) – влияние фактора
и внутригрупповая (De) – остальные причины.
Чем сильнее различаются групповые средние, тем больше Df .
Чем выше изменчивость внутри каждой группы, тем выше De.
Статистическая значимость определяется соотношением Df / De.
Величина эффекта:
© Наследов А. Д, 2012

Виды ANOVA и их специфические проблемы
Однофакторный ANOVA: множественные сравнения средних.
Многофакторный ANOVA: главные эффекты и взаимодействия факторов.
Многомерный ANOVA (MANOVA): применение многомерных критериев.
ANOVA с повторными измерениями: межгрупповые и внутригрупповые эффекты.
2 – 4: Общие Линейные Модели - ОЛМ (General Linear Models - GLM)
© Наследов А. Д, 2012

Коэффициент корреляции
r - мера вероятностной связи двух количественных переменных
© Наследов А. Д, 2012

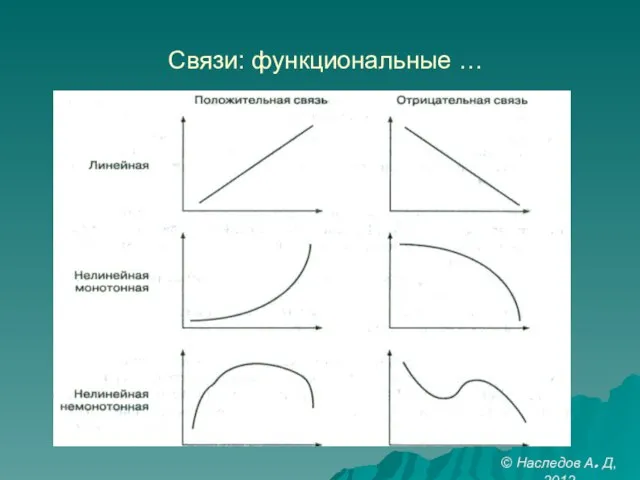
Связи: функциональные …
© Наследов А. Д, 2012

…и статистические
Коэффициент корреляции r это количественная мера
силы (абсолютное значение) и направления (знак)
вероятностной взаимосвязи двух переменных.
-1 ≤ r ≤ +1
© Наследов А. Д, 2012

Регрессия
yi — истинное i-значение Y,
— оценка i-значения Y по значению xi при помощи
линии (уравнения) регрессии,
ei = – ошибка оценки
Линия регрессии (прямая) аппроксимирует точки методом
наименьших квадратов:
Уравнение регрессии:
Коэффициент регрессии:
Свободный член:
© Наследов А. Д, 2012

Коэффициент детерминации
Дисперсия оценок зависимой переменной Y –
часть её дисперсии , обусловленная влиянием
независимой переменной X:
коэффициент детерминации,
доля дисперсии переменной Y (от 1),
«объясняемая» влиянием переменной X.
© Наследов А. Д, 2012

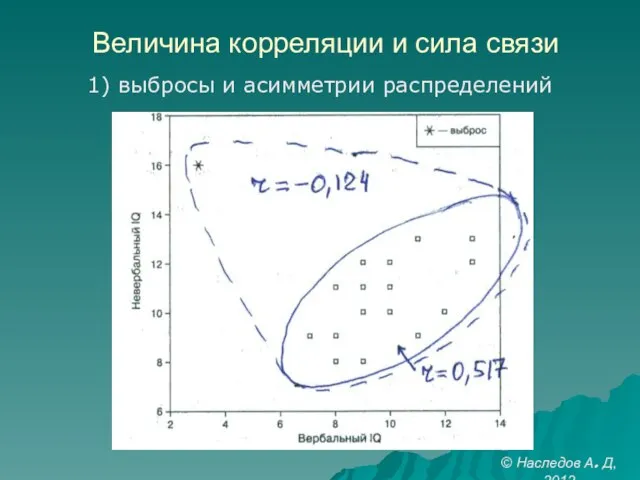
Величина корреляции и сила связи
1) выбросы и асимметрии распределений
© Наследов А. Д, 2012

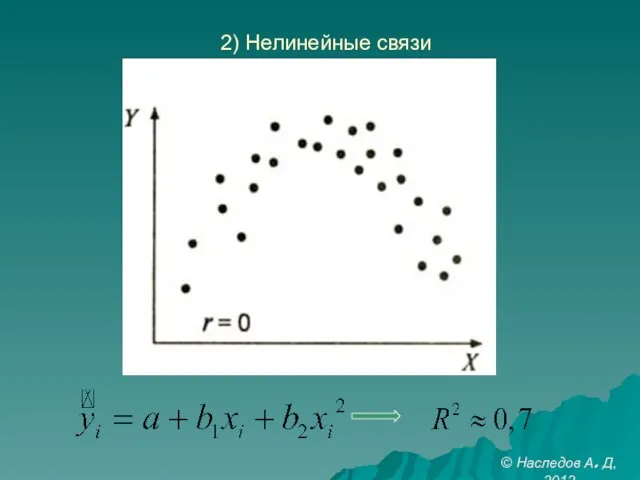
2) Нелинейные связи
© Наследов А. Д, 2012

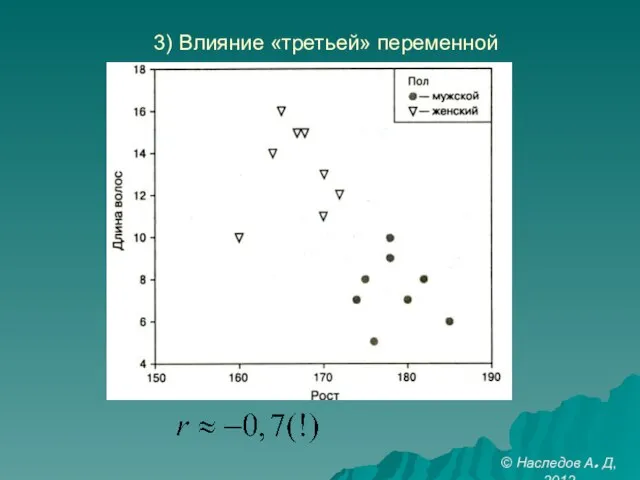
3) Влияние «третьей» переменной
© Наследов А. Д, 2012

Частная корреляция
Корреляция IQ (x) и длины стопы (y)
но корреляция IQ с возрастом (z)
а корреляция возраста и длины стопы
© Наследов А. Д, 2012

Ранговые корреляции
Вычисляются после замены исходных
значений рангами.
r-Спирмена, аналог r-Пирсона, основан на разности рангов
τ-Кендалла, вероятностный, основан на подсчете совпадений и инверсий в парах наблюдений.
© Наследов А. Д, 2012

Оцените величину корреляции без вычислений
1)
2)
3)
4)
5)
6)
1 и 2 – чему равен ϕ-сопряженности? r-Пирсона? ранговая корреляция?
3 - 6 – чему равен r-Пирсона? ранговая корреляция?
Варианты ответов:
а) = 1; б) = -1; в) отрицательный, но > -1; г) положительный, но < 1.
© Наследов А. Д, 2012

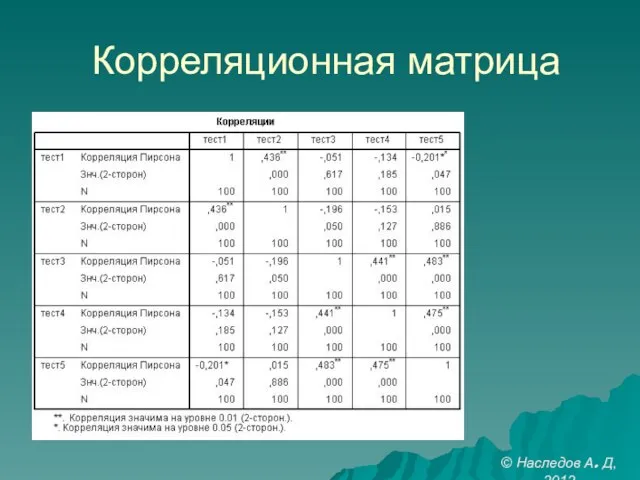
Последовательность интерпретации корреляций
Статистическая значимость (p-уровень).
Знак (направление).
Величина (по r-квадрат).
Числовые показатели: r = …; N = …; p = … .
ПРИМЕР. Для проверки гипотезы … применялась корреляция Пирсона.
Обнаружена статистически достоверная отрицательная корреляция
показателей тревожности и креативности (r = -0,435; N = 32; p = 0,035):
чем выше тревожность, тем ниже креативность.
© Наследов А. Д, 2012

Корреляционная матрица
© Наследов А. Д, 2012

Поправка Benjamini & Hochberg (1995)
для семейства n гипотез
Упорядочиваем все p от min до max (i – текущий номер p в ряду);
Для каждого i вычисляем: p*n/i = pкорр.;
Если pкорр.≤ α – результат статистически достоверен!
© Наследов А. Д, 2012