Арифметические и логические основы ПК

Система счисления — это совокупность приемов и правил записи и считывания чисел
Позиционные;
Непозиционные с/сч.
ХХХII
700 + 50 + 7 + 0,7 = 7•102 + 5•101 + 7•100 + 7•10-1 = 757,7.

Правила перевода целых чисел
— правило последовательного деления: Для перевода целой части из С.С. с основанием p в С.С. с основанием q необходимо делить исходную число и полученные значения частного на основание системы, в которую необходимо преобразовать данное число, представленное в С.С. p. Остатки от деления дают последовательность цифр представления целого числа в С.С. q. Запись числа в новой с.с. происходит с конца.

Правила перевода дробных чисел
Правило перевода дробной части — правило последовательного умножения: Для перевода правильной дроби из С.С. с основанием p в С.С. с основанием q необходимо умножить исходную дробь и дробные части получающихся произведений на основание системы в которую необходимо преобразовать данное число, представленное в С.С. p. Целые части получающихся произведений дают последовательность цифр представления дроби в С.С. q.
0.375 * 2 = 0.75 0 Старший Значащий Разряд (СЗР)
0.75 * 2 = 1.5 1
0.5 *2 = 1 1 Младший ЗР (МЗР)
Результат 0.011

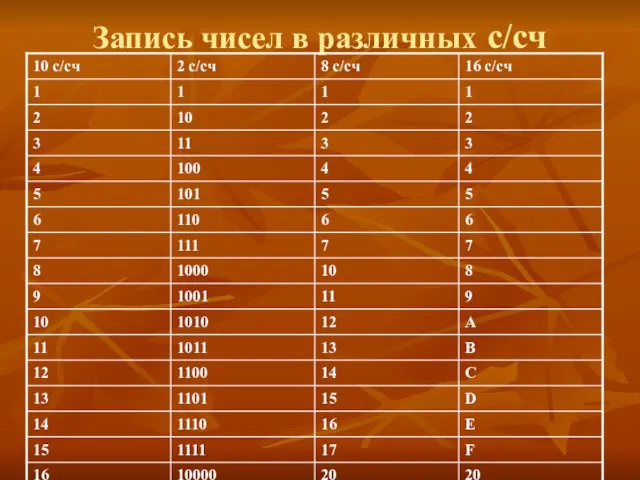
Запись чисел в различных с/сч

Представление чисел
с фиксированной точкой;
с плавающей точкой.
N=±M P±R,
где M – мантисса числа (|M|<1); R – порядок числа. Р – основание системы.
Нормализованным называют такое число, в старшем разряде мантиссы которого стоит единица.

Связь 8 и 16 с/сч с 2 с/сч
(537.1)8=(101 011 111.001)2
(1A3.F)16=(1 1010 0011.1111)16
Перевод получается заменой цифры на эквивалентную двоичную триаду или двоичную тетраду
Знак числа обычно кодируется двоичной цифрой, при этом 0 означает + (плюс), код 1 – знак минус (минус).

Сложение двоичных чисел
111012 =>1*24+1*23+1*22+1*20 =2710
+ 1112 =>1*22 +1*21 + 1*20 =710
_________
100100 => 1*25 +1*22 =3410

Вычитание двоичных чисел
100100 => 1*25 +1*22 =3410
- 1112 =>1*22 +1*21 + 1*20 =710
___________
111012 =>1*24+1*23+1*22+1*20 =2710

Двоичное умножение
А). Формирование первого частного произведения. Если значение младшего значащего разряда множителя равно 0, то и результат равен 0, если значение этого разряда равно 1, то результат является копией множимого.
Б). Правило сдвига. При использовании очередного разряда множителя для формирования частного произведения производится сдвиг множимого на один разряд (позицию) влево.
В). Правило сложения. Каждый раз, когда значение разряда множителя равно 1, к результату необходимо прибавить множимое, расположенное в позиции, определенной правилом сдвига.
Г). Определение результирующего произведения. Искомое произведение есть результат выполнения всех операций сдвига и сложения.

Умножение двоичных чисел
1112 =>1*22 +1*21 + 1*20 =710
* 1012 =>1*22 + 1*20 =510
_____________
111
+111
___________
1000112=> 1*25 +1*21 + 1*20 =3510

Деление двоичных чисел
1000112

Логические основы
Логической основой вычислительной техники является алгебра высказываний или булева алгебра. Она имеет свои законы, тождества и аксиомы. Разработана алгебра логики была Джорджем Булем в середине 19 века и названа в его честь.
Алгебра логики — это раздел математической логики, значения всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1.
Алгебра логики оперирует с логическими высказываниями

Высказывание
— это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности.
Логическое отрицание (инверсия) – НЕ;
Логическое сложение (дизъюнкция) – ИЛИ (+,v);
Логическое умножение (конъюнкция) – И (^,*);
Функция Вебба (отрицание дизъюнкции) – ИЛИ-НЕ;
Функция Шеффера (отрицание конъюнкции) – И-НЕ;
Импликация – операция, связанная связками «если …, то» - →;
Эквиваленция – операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «равносильно…» - ↔ или 
Сложение по модулю 2 (М2).

Эквиваленция, выраженная через отрицание, дизъюнкцию и конъюнкцию
Импликация, выраженная через дизъюнкцию и отрицание
А → В =
Физической моделью операции «И» является последовательное включение двух транзисторов в цепи. Цепь замкнута при работе обоих транзисторов.
Физической моделью операции «ИЛИ» является параллельное включение двух транзисторов в цепи.

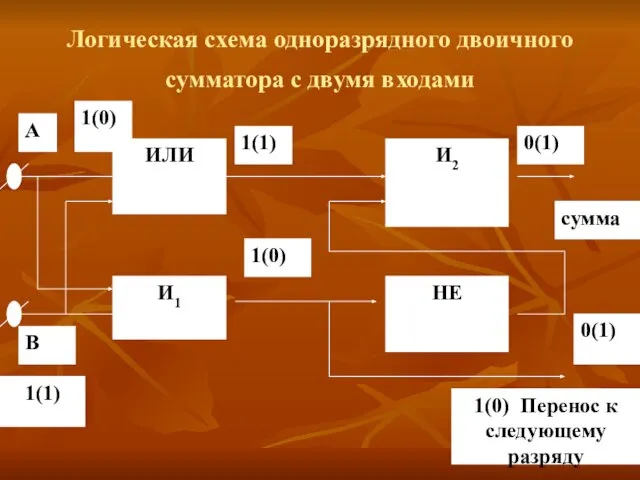
Логическая схема одноразрядного двоичного сумматора с двумя входами