Содержание
- 2. Арифметический квадратный корень Определение: арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен
- 3. Арифметический квадратный корень из числа а обозначается так: √ а. Знак √ называется знаком арифметического квадратного
- 4. Итак, выражение √ а имеет смысл только при а ≥ 0. Определение квадратного корня можно кратко
- 5. Квадратный корень из степени Вычислим значение выражения √ а при а=3 и а=-3. По определению квадратного
- 6. Вместо того чтобы говорить, что равенство и √а² = |а| выполняется при любых значениях входящих в
- 7. Теорема 2. Если a>b>0, то √a> √b. В самом деле, если допустить, что √a ≤√b, то,
- 8. Квадратный корень из произведения Теорема. Если a≥0, b≥0, то √ab=√a √b т.е. корень из произведения неотрицательных
- 9. Квадратный корень из дроби Теорема. Если а ≥0, b>0,то т.е. корень из дроби равен корню из
- 11. Скачать презентацию








 Современные возможности пробиотической терапии в клинике внутренних болезней
Современные возможности пробиотической терапии в клинике внутренних болезней Территория смыслов
Территория смыслов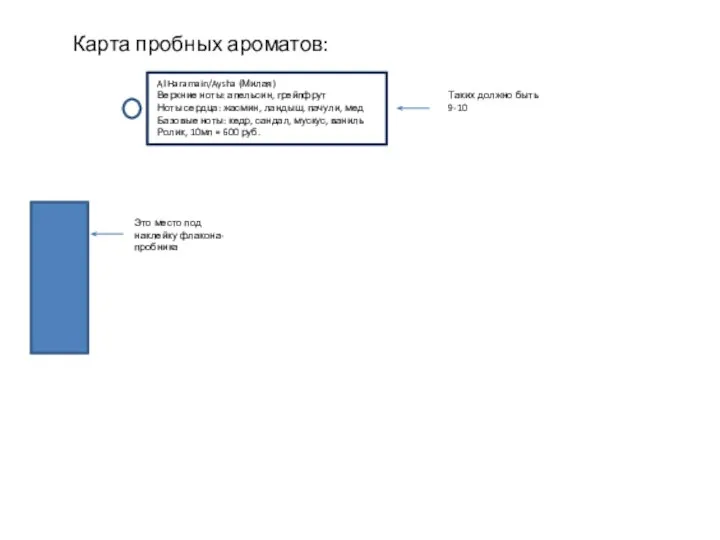 Карта пробных ароматов: Al Haramain/Aysha (милая)
Карта пробных ароматов: Al Haramain/Aysha (милая) Понятие мониторинга
Понятие мониторинга Прием письменного вычитания в случаях вида 50-24
Прием письменного вычитания в случаях вида 50-24 Акварельные зарисовки
Акварельные зарисовки Русские народные сказки
Русские народные сказки Красная книга растений
Красная книга растений Биография. Шаблон
Биография. Шаблон Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ
Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ Презентация на тему Телескоп
Презентация на тему Телескоп Презентация Сушильникова Н.И. Экологическая сказка
Презентация Сушильникова Н.И. Экологическая сказка Телеметрическая платформа M2MGate Solution
Телеметрическая платформа M2MGate Solution Китайский клуб МИИТа
Китайский клуб МИИТа Тема выпускной квалификационной работы. Шаблон
Тема выпускной квалификационной работы. Шаблон Морской порт Санкт-Петербург. Отчет по результатам линейного обхода
Морской порт Санкт-Петербург. Отчет по результатам линейного обхода С днем рождения!!!
С днем рождения!!! Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары
Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары Презентация на тему Климат Африки
Презентация на тему Климат Африки Коммуникативный практикум
Коммуникативный практикум Государство. Понятие. Теории происхождения
Государство. Понятие. Теории происхождения Жизнь прекрасна
Жизнь прекрасна Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода
Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода Венев
Венев ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ
ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ Экономия водоснабжения
Экономия водоснабжения Рифмоплёт
Рифмоплёт Вареники с картошкой
Вареники с картошкой