Биологические модели развития популяций

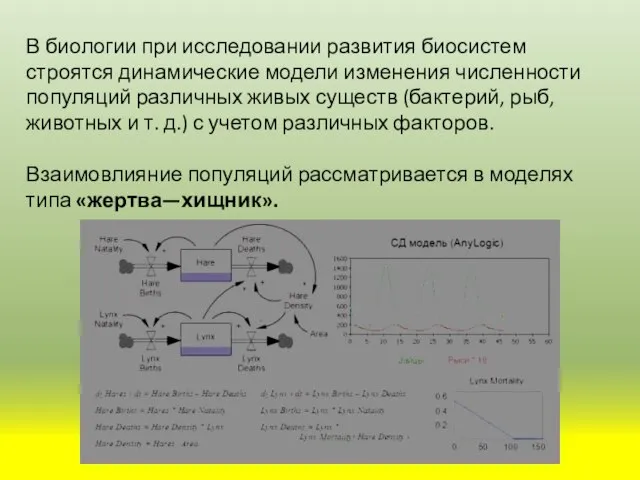
В биологии при исследовании развития биосистем строятся динамические модели изменения численности популяций различных живых существ (бактерий, рыб, животных и т. д.) с учетом различных факторов.
Взаимовлияние популяций рассматривается в моделях типа «жертва—хищник».

Формальная модель «Численность популяций»
Изучение динамики популяций естественно начать с простейшей модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент.
Математическую модель можно записать с помощью рекуррентной формулы, связывающей численность популяции следующего года с численностью популяции текущего года, с использованием коэффициента роста а:
Например, если ежегодный прирост численности популяции составляет 5%, то а = 1,05.

В модели ограниченного роста учитывается эффект перенаселенности, связанный с нехваткой питания, болезнями и т.д., который замедляет рост популяции с увеличением ее численности.
Введем коэффициент перенаселенности b, значение которого обычно существенно меньше а (b << а).
Тогда, коэффициент ежегодного увеличения численности равен (а-b*хn) и формула принимает вид:

В модели ограниченного роста с отловом учитывается, что на численность популяций промысловых животных и рыб оказывает влияние величина ежегодного отлова.
Если величина ежегодного отлова равна с, то формула принимает вид:

Популяции обычно существуют не изолированно, а во взаимодействии с другими популяциями.
Наиболее важным типом взаимодействия является взаимодействие между жертвами и хищниками (например, караси-щуки, зайцы-волки и т. д.).
В модели «жертва-хищник» количество жертв хn и количество хищников уn связаны между собой.
Количество встреч жертв с хищниками можно считать пропорциональной произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищниками. В этом случае численность популяции жертв уменьшается на величину f*Xn*yn и формула для расчета численности жертв принимает вид:

Численность популяции хищников в отсутствие жертв (в связи с отсутствием пищи) уменьшается, что можно описать рекуррентной формулой:
где значение коэффициента d < 1 характеризует скорость уменьшения численности популяции хищников.

Увеличение популяции хищников можно считать пропорциональной произведению количеств жертв и хищников, а коэффициент е характеризует величину роста численности хищников за счет жертв.
Тогда для численности хищников можно использовать формулу: