Содержание
- 2. What is Capital Budgeting (CB)? The process of identifying, analyzing, and selecting investment projects whose cash
- 3. The Capital Budgeting Process Generate investment proposals consistent with the firm’s strategic objectives. Estimate after-tax cash
- 4. The Capital Budgeting Process Select projects based on a value-maximizing acceptance criterion. Reevaluate implemented investment projects
- 5. Investment Project Proposals 1. New products or product modifications Replacement of existing equipment or buildings Real
- 6. Estimating After-Tax Incremental Cash Flows Cash (not accounting income) flows Excluding financing costs After-tax flows Incremental
- 7. Estimating After-Tax Incremental Cash Flows Ignore sunk costs Include project-driven changes in working capital Include effects
- 8. Calculating the Incremental Cash Flows Initial cash outflow - the initial net cash investment. Interim incremental
- 9. FCF = EBIT* Tax rate (%) = NOPLAT + Depreciation -/+ ∆NWC (+/- ∆AR +/- ∆Inventory
- 10. Initial Cash Outflow, ICO a) Cost of “new” assets b) + Capitalized expenditures c) + (-)
- 11. Terminal-Year Incremental Cash Flows a) Calculate the incremental net cash flow for the terminal period b)
- 12. Project Evaluation: Alternative Methods Payback Period (PBP) Discounted PBP (DPBP) Internal Rate of Return (IRR) Net
- 13. Proposed Project Data Julie is evaluating a new project for her firm, Basket Wonders (BW). She
- 14. Payback Period (PBP) PBP is the period of time required for the cumulative expected cash flows
- 15. (c) 10 K 22 K 37 K 47 K 54 K Payback Solution (#1) PBP =
- 16. Payback Solution (#2) PBP = 3 + ( 3K ) / 10K = 3.30 Years Note:
- 17. PBP Acceptance Criterion Yes! The firm will receive back the initial cash outlay in less than
- 18. The PBP Method Strengths and Weaknesses Strengths: Easy to use and understand Can be used as
- 19. Internal Rate of Return (IRR) IRR is the discount rate that equates the PV of the
- 20. $15,000 $10,000 $7,000 IRR Solution $10,000 $12,000 (1+IRR)1 (1+IRR)2 Need to find the interest rate (=IRR)
- 21. IRR Solution (Try 10%) $40,000 = $10,000(PVIF10%,1) + $12,000(PVIF10%,2) + $15,000(PVIF10%,3) + $10,000(PVIF10%,4) + $ 7,000(PVIF10%,5)
- 22. IRR Solution (Try 15%) $40,000 = $10,000(PVIF15%,1) + $12,000(PVIF15%,2) + $15,000(PVIF15%,3) + $10,000(PVIF15%,4) + $ 7,000(PVIF15%,5)
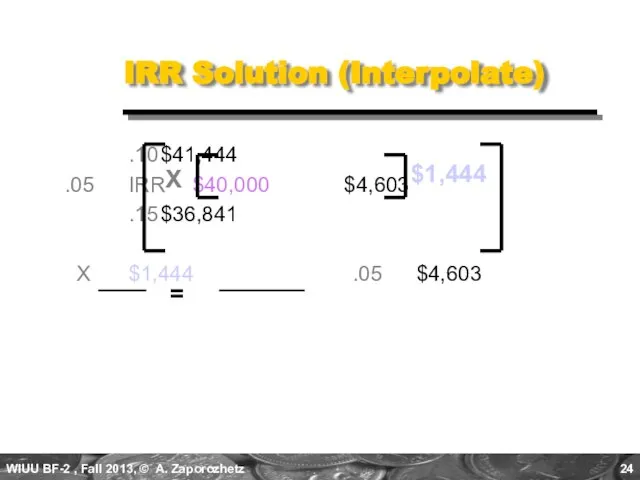
- 23. 0.10 $41,444 0.05 IRR $40,000 $4,603 0.15 $36,841 X $1,444 0.05 $4,603 IRR Solution (Interpolate) $1,444
- 24. .10 $41,444 .05 IRR $40,000 $4,603 .15 $36,841 X $1,444 .05 $4,603 IRR Solution (Interpolate) $1,444
- 25. 0.10 $41,444 0.05 IRR $40,000 $4,603 0.15 $36,841 ($1,444)(0.05) $4,603 IRR Solution (Interpolate) $1,444 X X
- 26. IRR Acceptance Criterion No! The firm will “receive” 11.57% for each dollar “required” for this project
- 27. IRR Strengths and Weaknesses Strengths: Accounts for TVM Considers all the cash flows Less subjectivity Weaknesses:
- 28. Net Present Value (NPV) NPV is the present value of an investment project’s net DCFs minus
- 29. Basket Wonders has determined that the appropriate discount rate (k) for this project is 13%. $10,000
- 30. NPV Solution NPV = $10,000(PVIF13%,1) + $12,000(PVIF13%,2) + $15,000(PVIF13%,3) + $10,000(PVIF13%,4) + $ 7,000(PVIF13%,5) - $40,000
- 31. NPV Acceptance Criterion No! The NPV is negative. This means that the project is reducing shareholder
- 32. NPV Strengths and Weaknesses Strengths: (Cash flows assumed to be reinvested at the hurdle rate.) Accounts
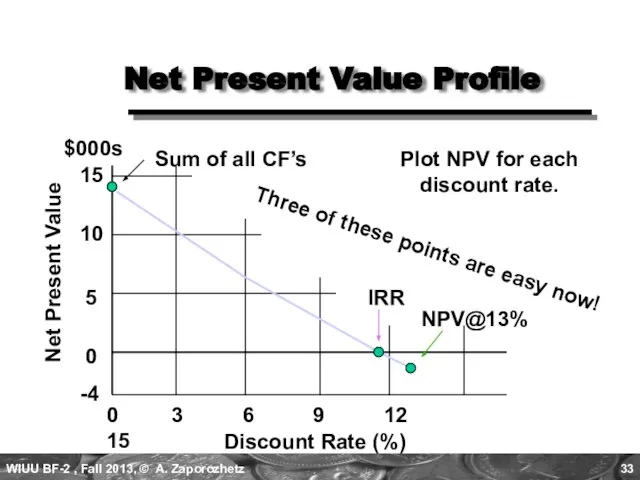
- 33. Net Present Value Profile Discount Rate (%) 0 3 6 9 12 15 IRR NPV@13% Sum
- 34. Profitability Index (PI) PI is the ratio of the present value of a project’s future net
- 35. PI Acceptance Criterion No! The PI is less than 1.00. This means that the project is
- 36. PI Strengths and Weaknesses Strengths: Same as NPV Allows for comparison of different scale and lifetime
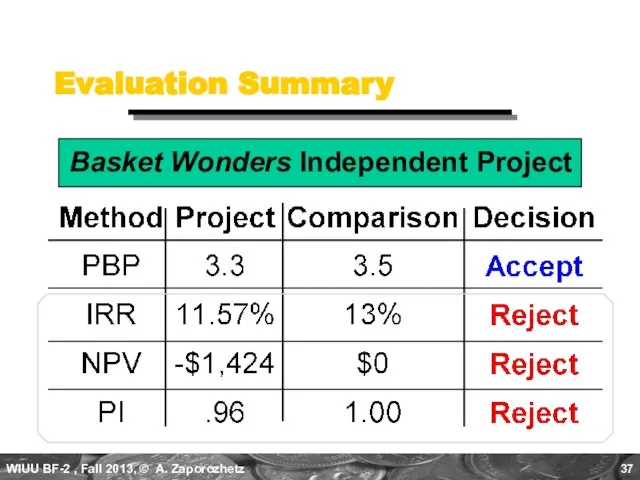
- 37. Evaluation Summary Basket Wonders Independent Project
- 38. Other Project Relationships Mutually Exclusive - A project whose acceptance precludes the acceptance of one or
- 39. Potential Problems Under Mutual Exclusivity A. Scale of Investment B. Cash-flow Pattern C. Project Life Ranking
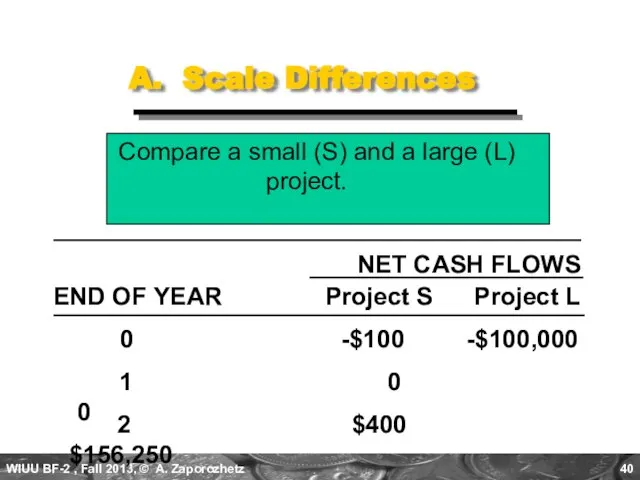
- 40. A. Scale Differences Compare a small (S) and a large (L) project. NET CASH FLOWS Project
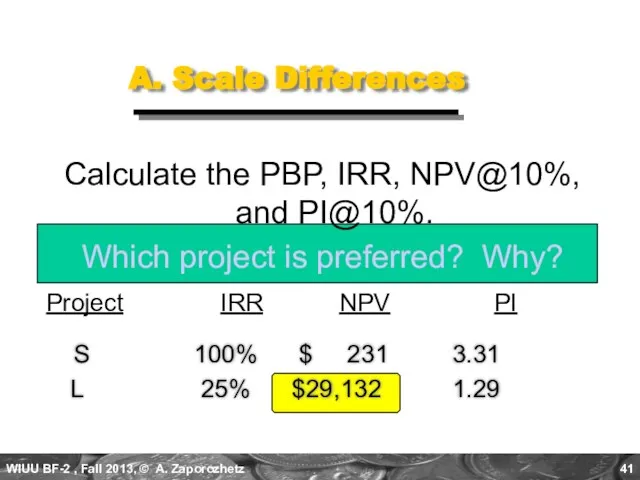
- 41. A. Scale Differences Calculate the PBP, IRR, NPV@10%, and PI@10%. Which project is preferred? Why? Project
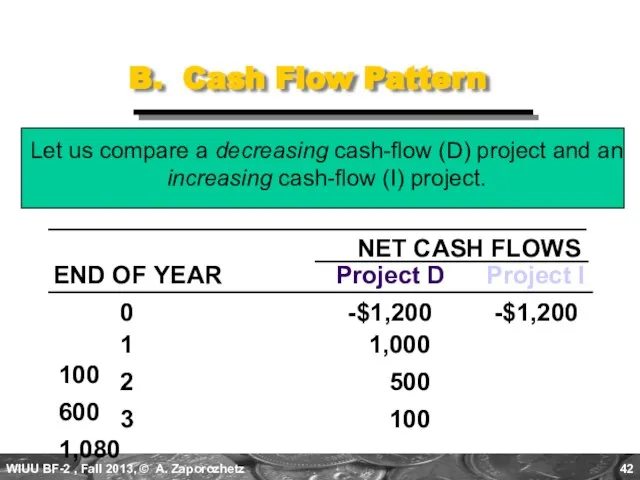
- 42. B. Cash Flow Pattern Let us compare a decreasing cash-flow (D) project and an increasing cash-flow
- 43. D 23% $197 1.16 I 17% $198 1.17 Cash Flow Pattern Calculate the IRR, NPV@10%, and
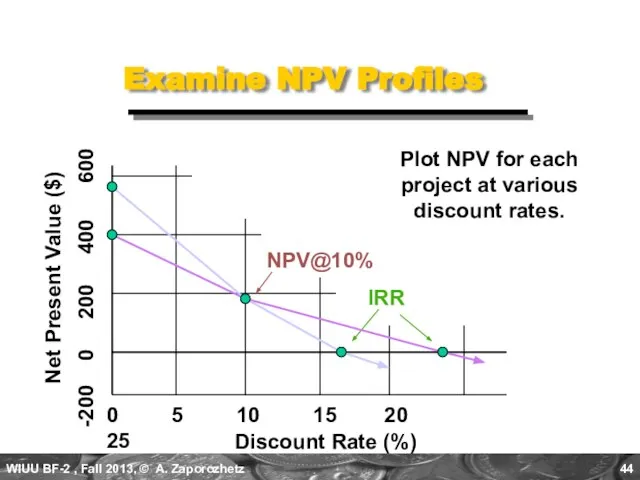
- 44. Examine NPV Profiles Discount Rate (%) 0 5 10 15 20 25 -200 0 200 400
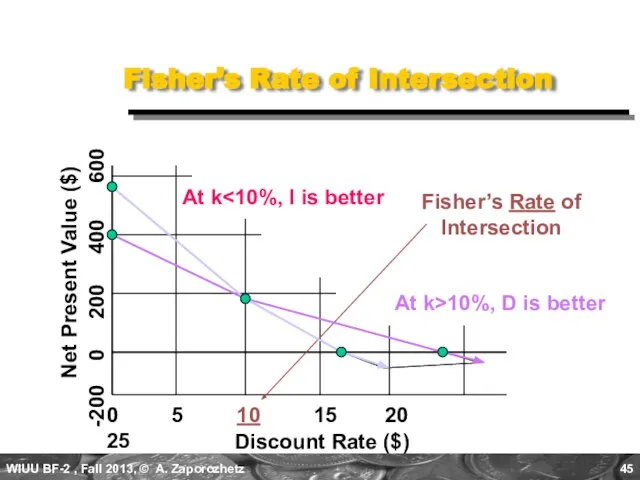
- 45. Fisher’s Rate of Intersection Discount Rate ($) 0 5 10 15 20 25 -200 0 200
- 46. C. Project Life Differences Let us compare a long life (X) project and a short life
- 47. X 50% $1,536 2.54 Y 100% $ 818 1.82 Project Life Differences Calculate the PBP, IRR,
- 48. Another Way to Look at Things 1. Adjust cash flows to a common terminal year if
- 49. Replacing Projects with Identical Projects 2. Use Replacement Chain Approach (Appendix B) when project “Y” will
- 50. Capital Rationing Capital Rationing occurs when a constraint (or budget ceiling) is placed on the total
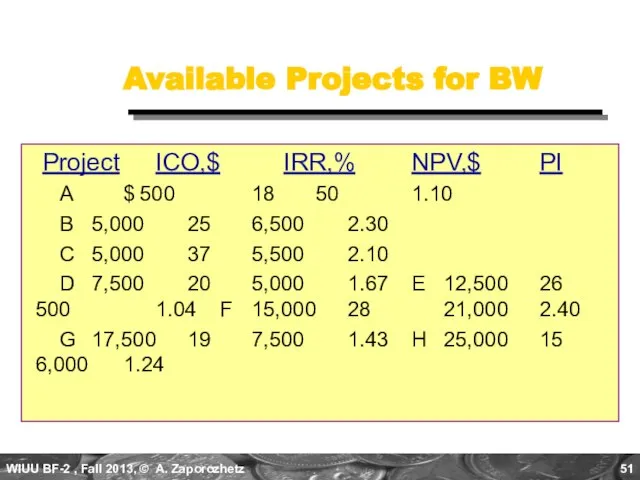
- 51. Available Projects for BW Project ICO,$ IRR,% NPV,$ PI A $ 500 18 50 1.10 B
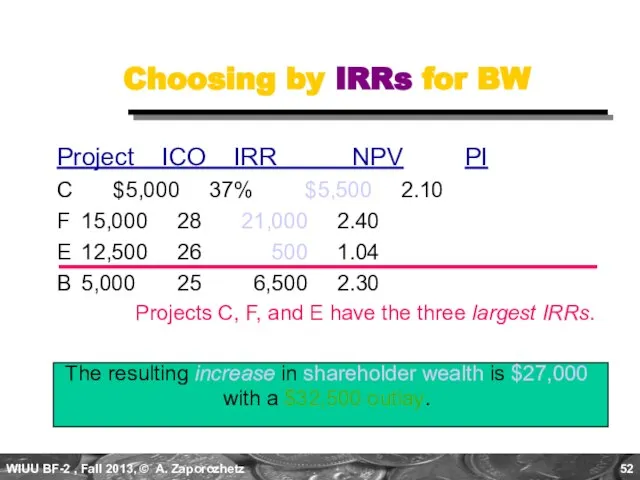
- 52. Choosing by IRRs for BW Project ICO IRR NPV PI C $5,000 37% $5,500 2.10 F
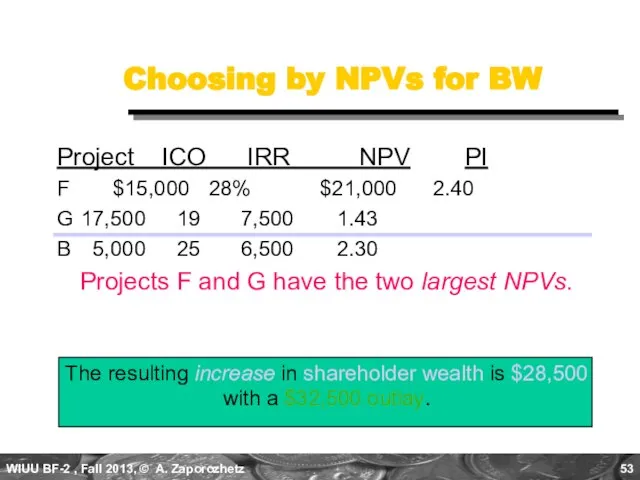
- 53. Choosing by NPVs for BW Project ICO IRR NPV PI F $15,000 28% $21,000 2.40 G
- 54. Choosing by PIs for BW Project ICO IRR NPV PI F $15,000 28% $21,000 2.40 B
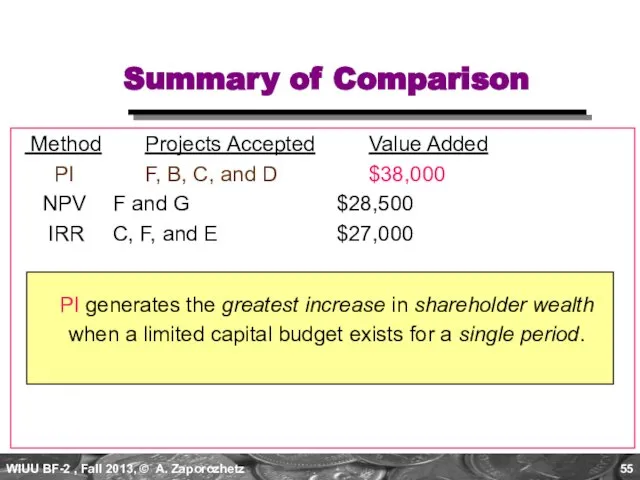
- 55. Summary of Comparison Method Projects Accepted Value Added PI F, B, C, and D $38,000 NPV
- 56. Post-Completion Audit: Usus Magister Est Optimus Post-completion Audit A formal comparison of the actual costs and
- 57. Multiple IRR Problem Two!! There are as many potential IRRs as there are sign changes. Let
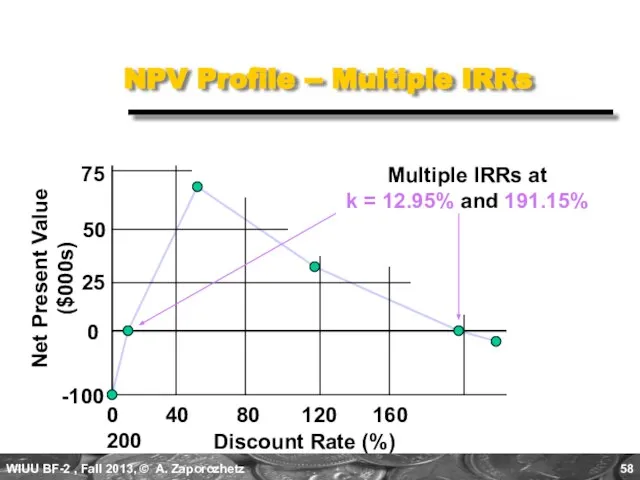
- 58. NPV Profile -- Multiple IRRs Discount Rate (%) 0 40 80 120 160 200 Net Present
- 60. Скачать презентацию












































 Творческое объединение лего-мастерская Шелезяка. Робототехника
Творческое объединение лего-мастерская Шелезяка. Робототехника Cовременные окрашивание волос
Cовременные окрашивание волос Veselaya_azbuka_10_09_16
Veselaya_azbuka_10_09_16 Bunker - лидеры рынка
Bunker - лидеры рынка Тестування Потреба відображає
Тестування Потреба відображає Что такое театр?
Что такое театр? Начало петровской эпохи
Начало петровской эпохи  Культурное наследие кочевников
Культурное наследие кочевников City (Город)
City (Город) Менеджер по рекламе
Менеджер по рекламе ДЕЛОПРОИЗВОДСТВЕНННЫЕ МАТЕРИАЛЫ
ДЕЛОПРОИЗВОДСТВЕНННЫЕ МАТЕРИАЛЫ Браузер- окно в мир Internet
Браузер- окно в мир Internet Золотое кольцо России
Золотое кольцо России методы когнитивного исследования (презентация Анны Киселевой)
методы когнитивного исследования (презентация Анны Киселевой) Идеи новогоднего макияжа
Идеи новогоднего макияжа Лекция Тема: «Зарубежный опыт организации государственной службы»
Лекция Тема: «Зарубежный опыт организации государственной службы» Главная улица Москвы Если вы пройдете через Александровский сад и повернете налево,
Главная улица Москвы Если вы пройдете через Александровский сад и повернете налево, Как вести себя в опасных ситуациях
Как вести себя в опасных ситуациях Презентация на тему Первые люди
Презентация на тему Первые люди  Холодная война
Холодная война ПРОСТРАНСТВО ДОМА В РУССКОМ ЯЗЫКОВОМ СОЗНАНИИ
ПРОСТРАНСТВО ДОМА В РУССКОМ ЯЗЫКОВОМ СОЗНАНИИ Ниточный дизайн
Ниточный дизайн Формирование соединений при сварке давлением. (Лекция 2)
Формирование соединений при сварке давлением. (Лекция 2) Медициналық ортадағы кикілжің
Медициналық ортадағы кикілжің Латунь в машиностроении
Латунь в машиностроении Сотовый телефон. Вреден ли он для здоровья 4 класс
Сотовый телефон. Вреден ли он для здоровья 4 класс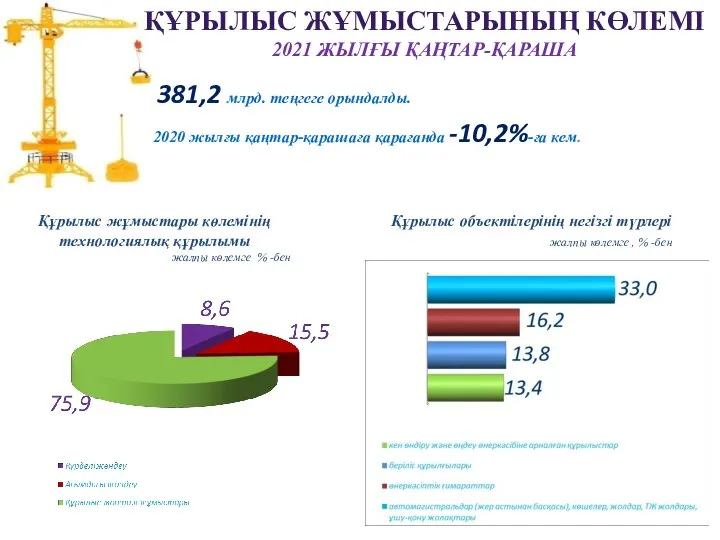 Подряд_KZ_11.21
Подряд_KZ_11.21 Африканская саванна
Африканская саванна