Содержание
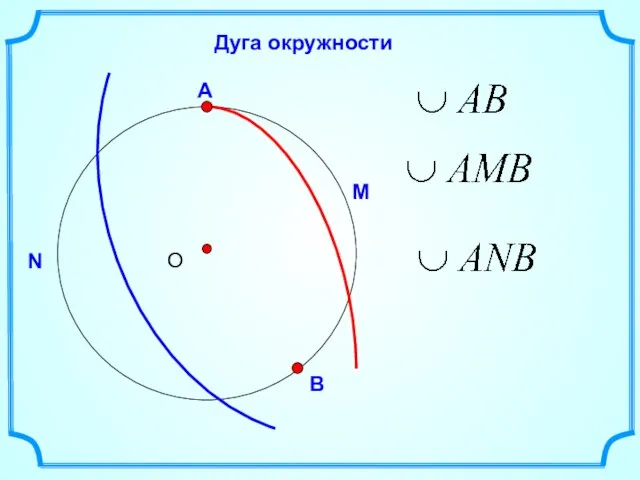
- 2. Дуга окружности М
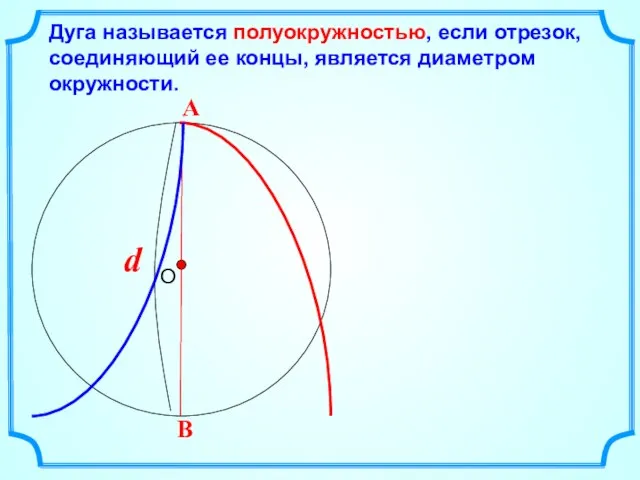
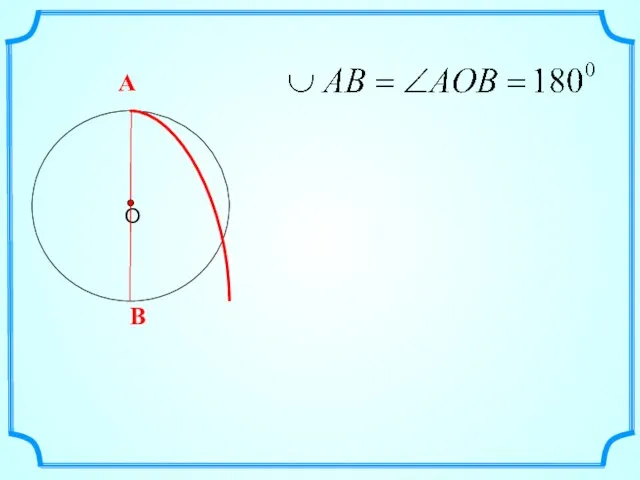
- 3. Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.
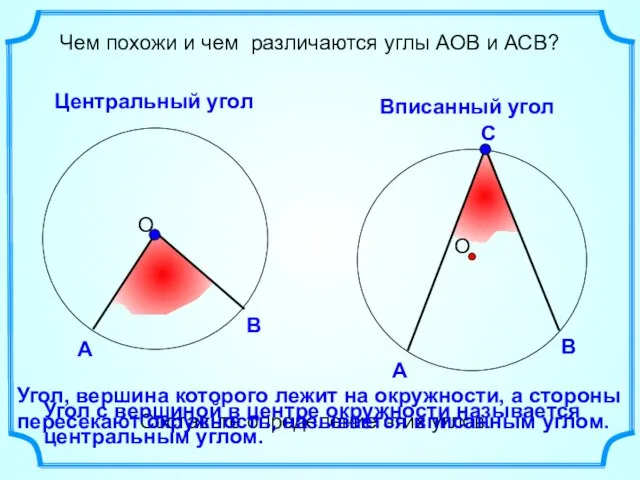
- 4. Чем похожи и чем различаются углы АОВ и АСВ? Центральный угол Вписанный угол Составьте определение этих
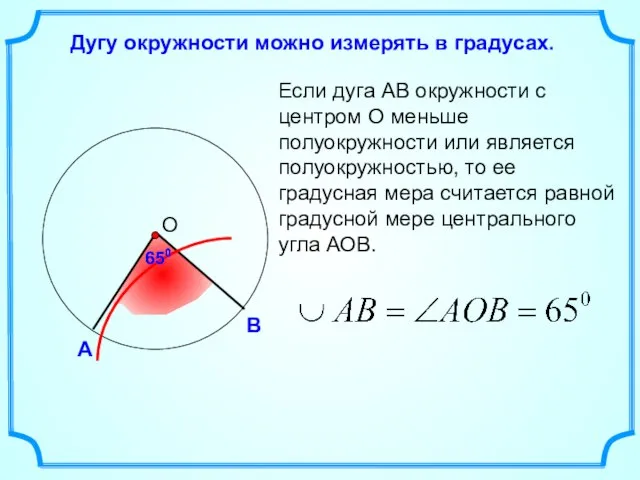
- 5. Дугу окружности можно измерять в градусах. Если дуга АВ окружности с центром О меньше полуокружности или
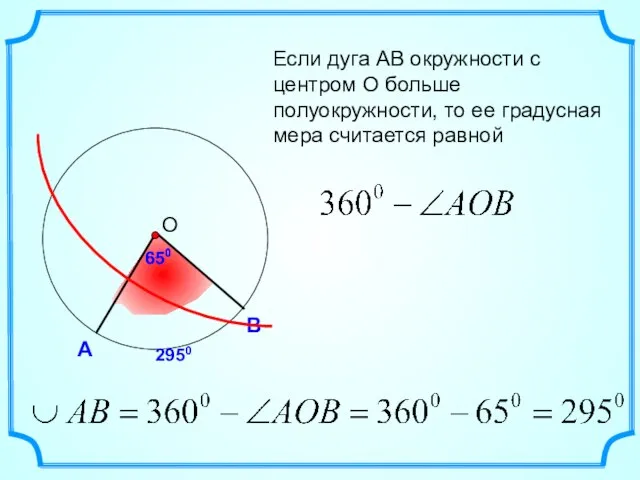
- 7. А В Если дуга АВ окружности с центром О больше полуокружности, то ее градусная мера считается
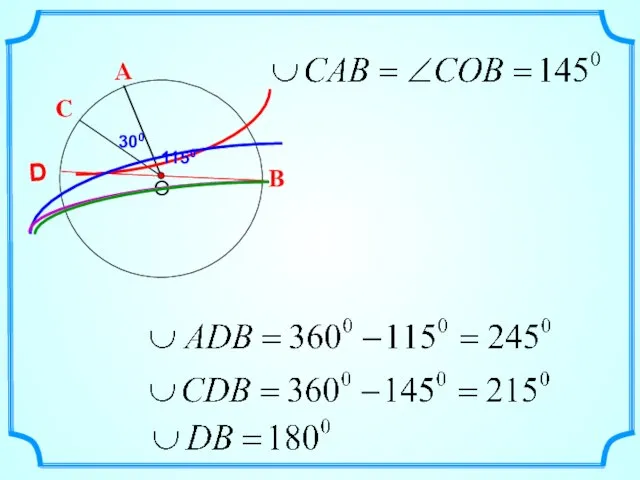
- 8. А В С D 1150 300
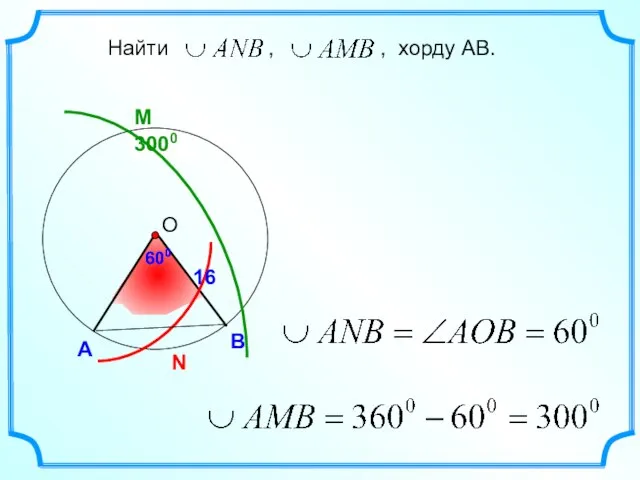
- 9. M 3000 600 А В Найти , , хорду АВ. 600 N 16
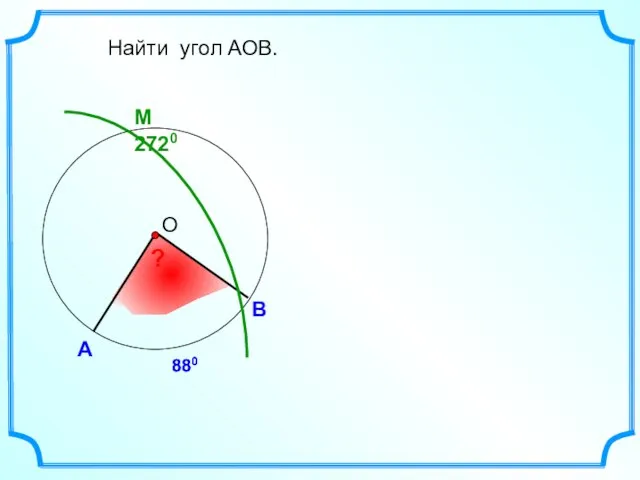
- 10. M 2720 880 А В Найти угол АОВ. ? 880
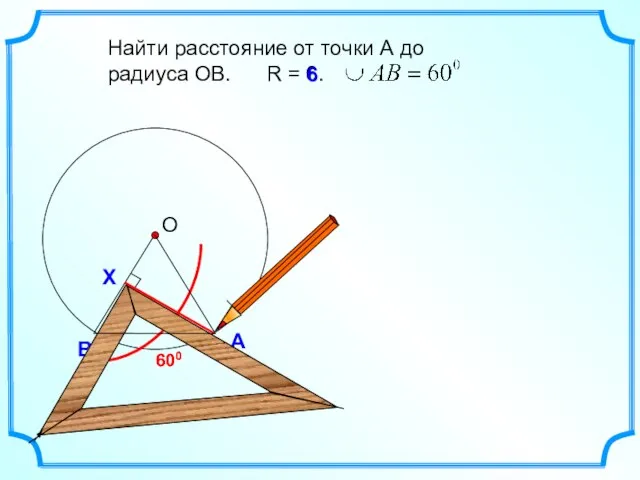
- 11. В А Найти расстояние от точки А до радиуса ОВ. R = 6. 600 600 6
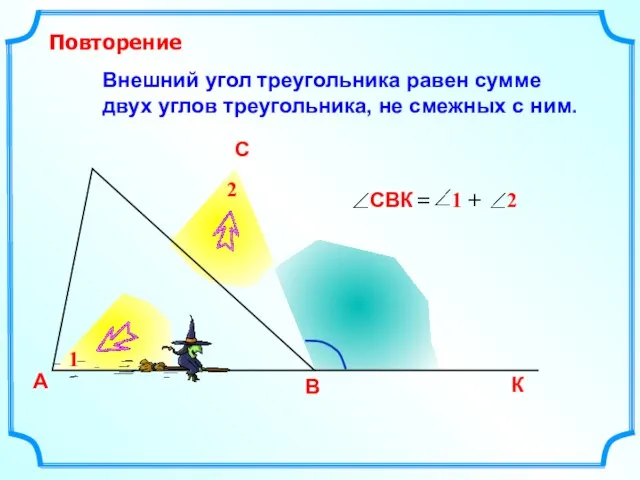
- 12. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. А В С К
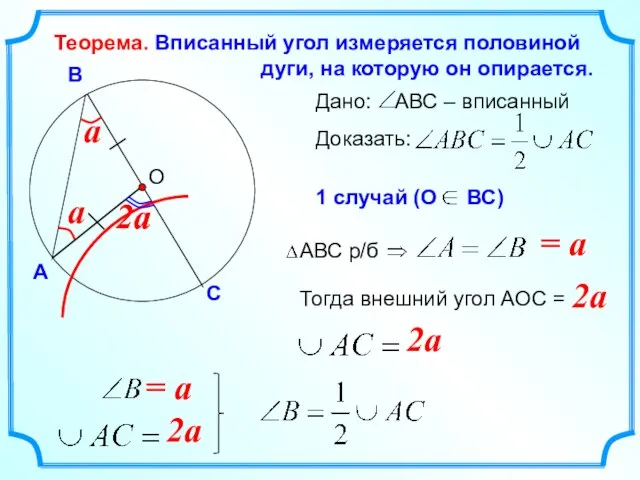
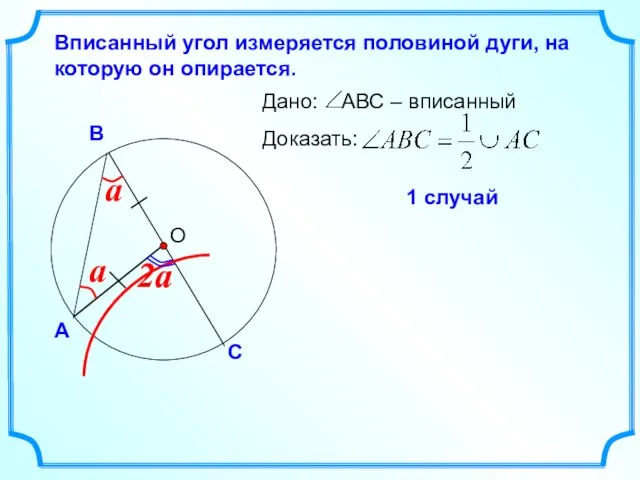
- 13. О Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. 2a 2a = a 2a
- 14. О Вписанный угол измеряется половиной дуги, на которую он опирается. 1 случай 2a 2a
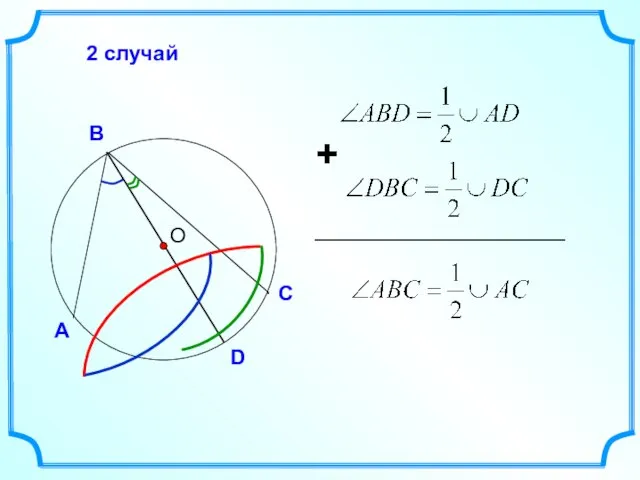
- 15. О А С В 2 случай D
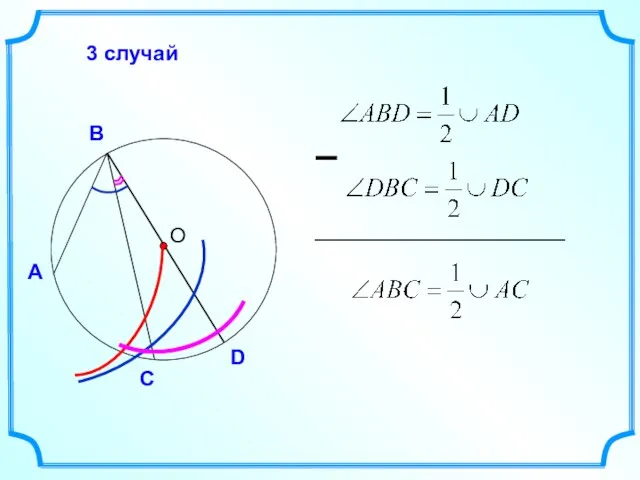
- 16. О А С В 3 случай D
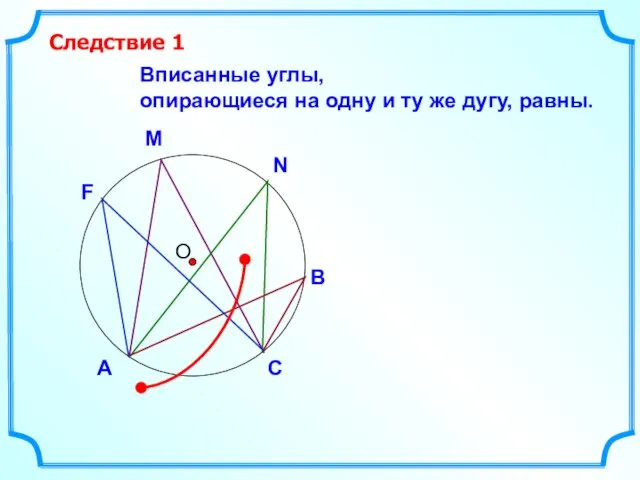
- 17. О Вписанные углы, опирающиеся на одну и ту же дугу, равны. Следствие 1 В N M
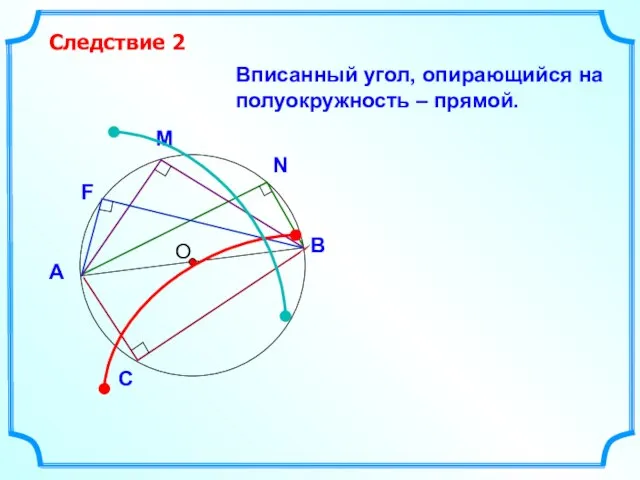
- 18. О Вписанный угол, опирающийся на полуокружность – прямой. Следствие 2 В А
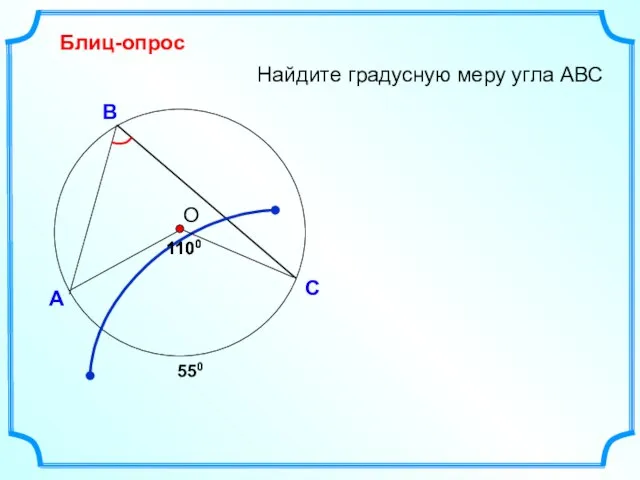
- 19. Блиц-опрос А С В Найдите градусную меру угла АВС 1100 О 1100 550
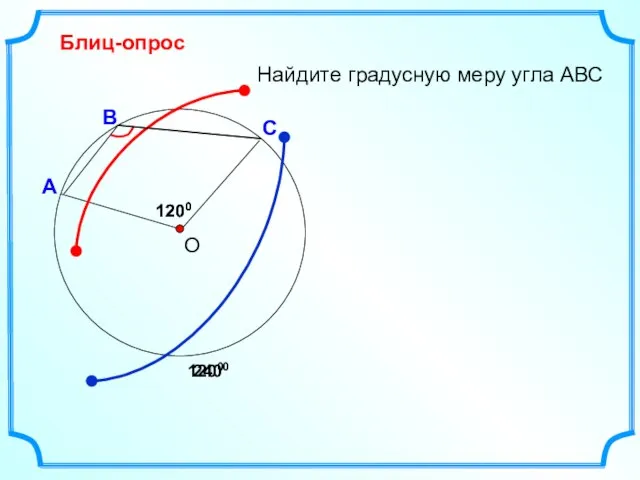
- 20. Блиц-опрос А С В Найдите градусную меру угла АВС 1200 О 1200 2400 1200
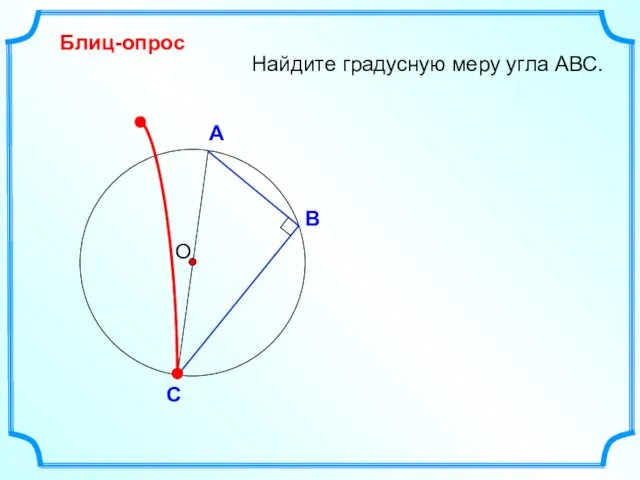
- 21. Найдите градусную меру угла АВС. О В А С Блиц-опрос
- 23. Скачать презентацию
 Баба яга и ягоды.
Баба яга и ягоды. Презентация на тему "Развивающая система Занкова Л.В" - скачать презентации по Педагогике
Презентация на тему "Развивающая система Занкова Л.В" - скачать презентации по Педагогике Презентация по бжд студентки 1 курса юб 1403 фоминой юлии
Презентация по бжд студентки 1 курса юб 1403 фоминой юлии Животные-космонавты!
Животные-космонавты! Средняя общеобразовательная школа №16 была открыта в 1965 году. В последующие годы школа повысила свой статус: в 1989 году школа получи
Средняя общеобразовательная школа №16 была открыта в 1965 году. В последующие годы школа повысила свой статус: в 1989 году школа получи Электрон
Электрон Стихотворные размеры
Стихотворные размеры Дарвин Чарлз Роберт
Дарвин Чарлз Роберт Аудит земель и электронные карты. Услуги и продажа уникальных летающих дронов
Аудит земель и электронные карты. Услуги и продажа уникальных летающих дронов Форма государства
Форма государства Творчество Ф.Б. Растрелли
Творчество Ф.Б. Растрелли Фрагментация СМИ и социальных медиа Александр Амзин.
Фрагментация СМИ и социальных медиа Александр Амзин. Устный счет в пределах 10
Устный счет в пределах 10 Презентация на тему Правописание НЕ с разными частями речи (10 класс)
Презентация на тему Правописание НЕ с разными частями речи (10 класс) Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа с. Новополеводино» Балаковского района Сарато
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа с. Новополеводино» Балаковского района Сарато Конституционные основы организации и деятельности Правительства Российской Федерации и иных федеральных органов
Конституционные основы организации и деятельности Правительства Российской Федерации и иных федеральных органов Класс Птицы. СОВООБРАЗНЫЕ
Класс Птицы. СОВООБРАЗНЫЕ Презентация на тему ЗАДАЧИ «Безработица»
Презентация на тему ЗАДАЧИ «Безработица»  The University of Toronto
The University of Toronto Аудит бухгалтерской (финансовой) отчетности страховой организации
Аудит бухгалтерской (финансовой) отчетности страховой организации Капитальный ремонт общего имущества многоквартирного дома за счет субсидий по 185-ФЗ от 21.07.2007 (часть 1)
Капитальный ремонт общего имущества многоквартирного дома за счет субсидий по 185-ФЗ от 21.07.2007 (часть 1) Бюджет IT проекта
Бюджет IT проекта Лук и чеснокРецепты красоты и здоровья
Лук и чеснокРецепты красоты и здоровья Классный час:
Классный час: Экскурсия по Алтайскому краю
Экскурсия по Алтайскому краю Особое мнение судьи Конституционного суда
Особое мнение судьи Конституционного суда Приключение снеговика
Приключение снеговика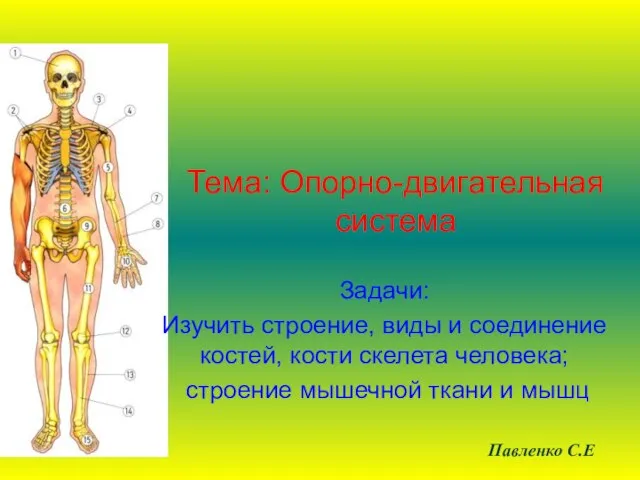 Опорно-двигательная система
Опорно-двигательная система