Слайд 2CAE-Services
Рассмотрена газодинамическая задача численного моделирования внешнего сверхзвукового и трансзвукового обтекания изделия, общий

вид которого представлен на слайде 3.
Численные расчеты проводились на персональном компьютере.
Для решения пространственных уравнений Навье-Стокса, описывающих сжимаемые вязкие турбулентные течения, использовался метод конечного объема, численная схема высокого порядка для конвективных и вязких членов, модель турбулентности SST k-ω, позволяющая моделировать течения с развитыми отрывными зонами.
Расчетная область представляла собой параллелепипед, грани которого удалены от поверхности обтекаемого изделия на 8 калибров.
На стенках параллелепипеда, моделирующего «бесконечную» расчетную область, заполненную потоком воздуха, использовались граничные условия типа “Inlet”, “Outlet” (для сверхзвуковых режимов), “Opening” (на дозвуковых режимах), “Symmetry” и ”Wall” (на боковых стенках).
Слайд 3CAE-Services
Изделие «Missile-77»
(ОАО Корпорация Тактическое Ракетное Вооружение)

Слайд 4CAE-Services
Построена пространственная неструктурированная гибридная сетка, состоящая из 107 607 узлов, 494 768

ячеек (485 248 тетраэдров, 9 044 гексаэдра, 476 пирамид), при этом на поверхности рассчитываемого изделия генерировалась треугольная сетка.
В области пограничного слоя в окрестности твердой поверхности тела и в местах резкого изменения кривизны поверхности (острые «носики» обтекателей и острые кромки на крыльях и оперении, слайды 5-6) делалось специальное «прижатие» и сгущение ячеек сетки.
Выбор такой топологии сетки обусловлен достаточно сложной геометрической формой изделия, для которой построение, например, многоблочной структурированной гексаэдральной сетки весьма проблематично.
Слайд 5CAE-Services
Пространственная неструктурированная гибридная сетка: 107 607 узлов,
494 768 ячеек (485 248

тетраэдров, 9 044 гексаэдра, 476 пирамид)
Слайд 6CAE-Services
Фрагмент треугольной сетки на поверхности изделия

Слайд 7CAE-Services
Численные расчеты распределенных и интегральных характеристик изделия (в схеме «крест») проводились для

угла атаки α=6° в диапазоне чисел Маха М=0.8-3.0 и чисел Рейнольдса Re=(24-90)·106.
Результаты расчетов, а также сравнение с имеющимися экспериментальными данными представлены на слайдах 8-12.
Как показал анализ расчетов, даже на достаточно «грубой» (порядка 100 тыс. узлов) неструктурированной гибридной сетке, построенной для изделия сложной конфигурации, удается получить достаточно достоверные численные результаты для интегральных аэродинамических характеристик, удовлетворительно согласующиеся с данными эксперимента.
Слайд 8CAE-Services
М=1.2, α=6° Распределение чисел Маха в плоскости симметрии
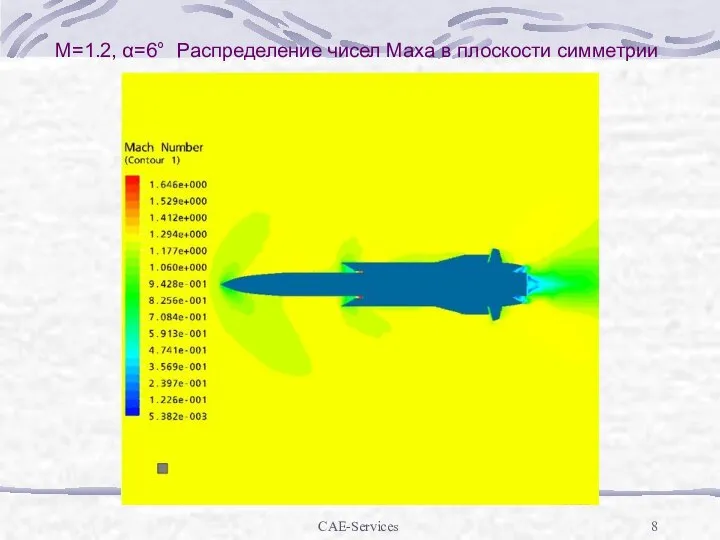
Слайд 9CAE-Services
М=3.0, α=6° Распределение чисел Маха в плоскости симметрии
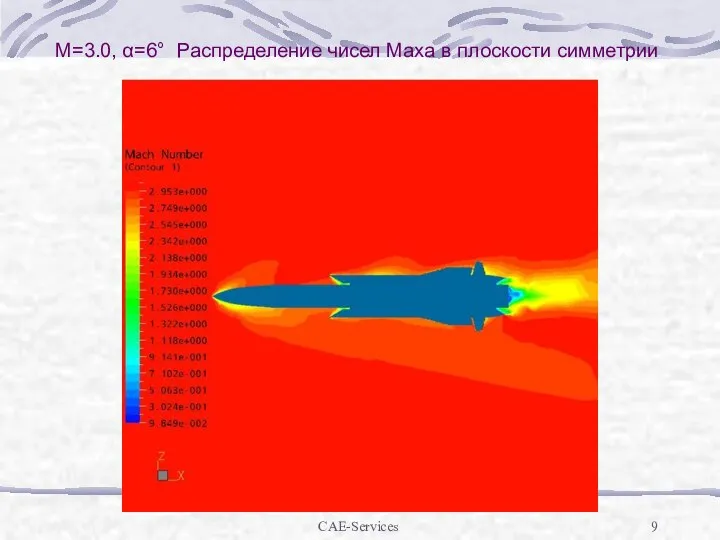
Слайд 10CAE-Services
М=3.0, α=6° Распределение давления на поверхности изделия

Слайд 11CAE-Services
Зависимость интегральных аэродинамических характеристик от числа Маха
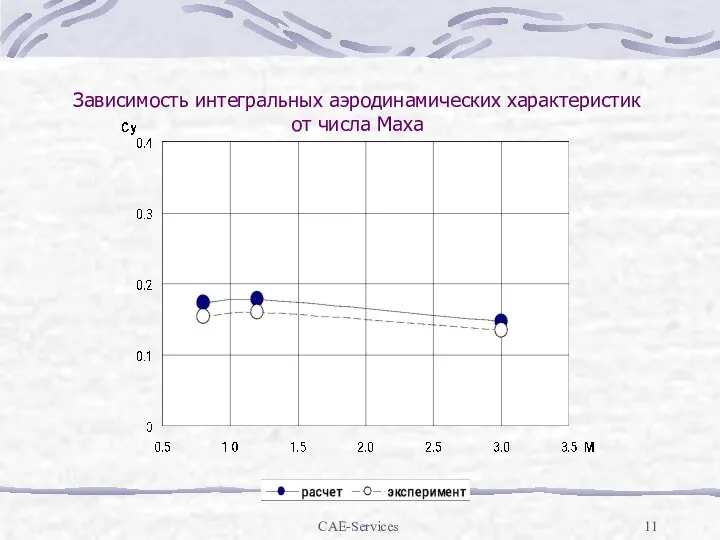
Слайд 12CAE-Services
Зависимость интегральных аэродинамических характеристик от числа Маха
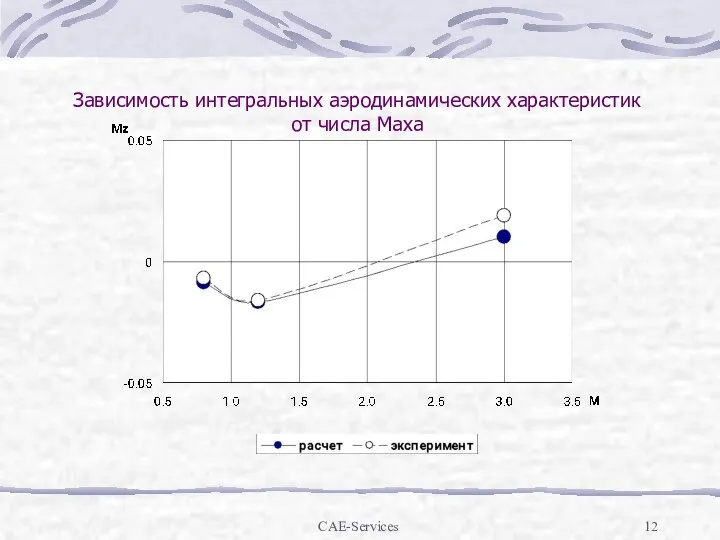











 Гражданское воспитание
Гражданское воспитание Золотое сечение
Золотое сечение Презентация на тему Рыба и морепродукты
Презентация на тему Рыба и морепродукты Конструирование темы и проблематики проекта. Проектный замысел. Новизна
Конструирование темы и проблематики проекта. Проектный замысел. Новизна 1 С 1 ноября 2011 г. авиакомпания Эль Аль вводит в действие новые правила оплаты сверхнормативного багажа Каждый пассажир экономическ
1 С 1 ноября 2011 г. авиакомпания Эль Аль вводит в действие новые правила оплаты сверхнормативного багажа Каждый пассажир экономическ Семченко Евгений Евгеньевич
Семченко Евгений Евгеньевич Настроение в школе
Настроение в школе Правописание Е- Ё после шипящих в суффиксах причастий
Правописание Е- Ё после шипящих в суффиксах причастий Презентация интерфейса ISS для бизнес-клиентов
Презентация интерфейса ISS для бизнес-клиентов 27 марта 2010 г. Санкт-Петербург
27 марта 2010 г. Санкт-Петербург Свойства функции на основе этнокультурного материала.
Свойства функции на основе этнокультурного материала. Масленица
Масленица Муниципальная модель конкурсной системы 12 месяцев – 12 конкурсов. Лето
Муниципальная модель конкурсной системы 12 месяцев – 12 конкурсов. Лето Техника изонити 1 урок
Техника изонити 1 урок Оценка персонала. Идеология оценки персонала
Оценка персонала. Идеология оценки персонала QUALITY OF LIFE
QUALITY OF LIFE  Искусство ХХ века в Третьяковке В будущее возьмут не всех
Искусство ХХ века в Третьяковке В будущее возьмут не всех Всемирный день спасибо
Всемирный день спасибо Презентация на тему Аграрная реформа П.А. Столыпина
Презентация на тему Аграрная реформа П.А. Столыпина  Влияние радиации на организмы
Влияние радиации на организмы Привет В зоопарке
Привет В зоопарке Жаргонизмы как языковое явление в речи
Жаргонизмы как языковое явление в речи b Magyarország romlása - Mohács
b Magyarország romlása - Mohács Развитие стран Западной Европы и США Во второй половине XX века
Развитие стран Западной Европы и США Во второй половине XX века Международный опыт внедренияMDM Server for PIM
Международный опыт внедренияMDM Server for PIM Презентация на тему Холодные блюда из рыбы
Презентация на тему Холодные блюда из рыбы Презентация бренда Даулет Даукенов
Презентация бренда Даулет Даукенов Шиповник -лекарство
Шиповник -лекарство