Ch1-LinEquations

Ch1_
Ch1_
Definition
An equation such as x+3y=9 is called a linear equation
(in two variables or unknowns).
The graph of this equation is a straight line in the xy-plane.
A pair of values of x and y that satisfy the equation is called a solution.
1.1 Matrices and Systems of Linear Equations

Ch1_
Ch1_
Definition
A linear equation in n variables x1, x2, x3, …, xn has the form a1 x1 + a2 x2 + a3 x3 + … + an xn = b
where the coefficients a1, a2, a3, …, an and b are real numbers.

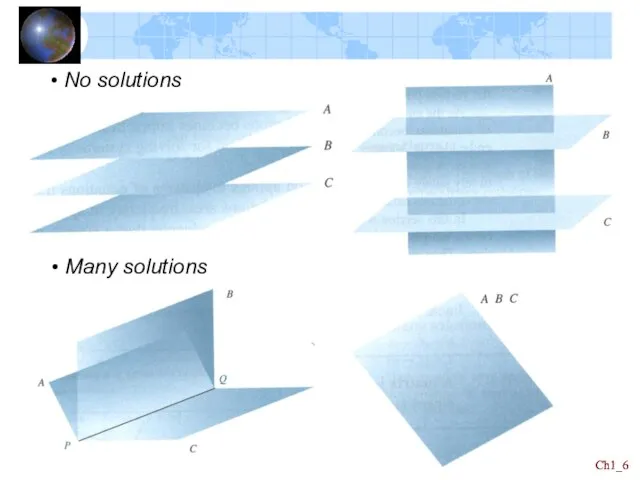
Ch1_
Ch1_
Solutions for system of linear equations
Figure 1.1
Unique solution
x + 3y = 9
–2x + y = –4
Lines intersect at (3, 2)
Unique solution: x = 3, y = 2.

Ch1_
Ch1_
A linear equation in three variables corresponds to
a plane in three-dimensional space.
※ Systems of three linear equations in three variables:

Ch1_
Ch1_

Ch1_
Ch1_
A solution to a system of a three linear equations will be points that lie on all three planes.
The following is an example of a system of three linear equations:
How to solve a system of linear equations? For this we introduce a method called Gauss-Jordan elimination. (Section1.2)

Ch1_
Ch1_
Definition
A matrix is a rectangular array of numbers.
The numbers in the array are called the elements of the matrix.
Matrices

Ch1_
Ch1_
Submatrix
Row and Column

Ch1_
Ch1_

Ch1_
Ch1_
matrix of coefficients and augmented matrix
Relations between system of linear equations and matrices

Ch1_
Ch1_
Elementary Transformation
Interchange two equations.
Multiply both sides of an equation by a nonzero constant.
Add a multiple of one equation to another equation.
Elementary Row Operation
Interchange two rows of a matrix.
Multiply the elements of a row by a nonzero constant.
Add a multiple of the elements of one row to the corresponding elements of another row.
Elementary Row Operations of Matrices

Ch1_
Ch1_
Example 1
Solving the following system of linear equation.

Ch1_
Ch1_

Ch1_
Ch1_
Example 2
Solving the following system of linear equation.
Solution

Ch1_
Ch1_
Example 3
Solve the system
Solution

Ch1_
Ch1_
Summary
Use row operations to [A: B] :
Def. [In : X] is called the reduced echelon form of [A : B].
Note. 1. If A is the matrix of coefficients of a system of n equations in n variables that has a unique solution,
then A is row equivalent to In (A ≈ In).
2. If A ≈ In, then the system has unique solution.

Ch1_
Ch1_
Example 4 Many Systems
Solving the following three systems of linear equation, all of which have the same matrix of coefficients.
Solution
The solutions to
the three systems are

Ch1_
Ch1_
Homework
Exercises will be given by the teachers of the practical classes.

Ch1_
Ch1_
1.2 Gauss-Jordan Elimination
Definition
A matrix is in reduced echelon form if
Any rows consisting entirely of zeros are grouped at the bottom of the matrix.
The first nonzero element of each other row is 1. This element is called a leading 1.
The leading 1 of each row after the first is positioned to the right of the leading 1 of the previous row.
All other elements in a column that contains a leading 1 are zero.

Ch1_
Ch1_
Examples for reduced echelon form
(✓)
(✓)
(?)
(?)
elementary row operations，reduced echelon form
The reduced echelon form of a matrix is unique.

Ch1_
Ch1_
Gauss-Jordan Elimination
System of linear equations
⇒ augmented matrix
⇒ reduced echelon form
⇒ solution

Ch1_
Ch1_
Example 1
Use the method of Gauss-Jordan elimination to find reduced echelon form of the following matrix.
Solution
The matrix is the reduced echelon form of the given matrix.

Ch1_
Ch1_
Example 2
Solve, if possible, the system of equations
Solution
The general solution to the system is

Ch1_
Ch1_
Example 3
Solve the system of equations
Solution
⇒ many sol.

Ch1_
Ch1_
Example 4
Solve the system of equations
Solution

Ch1_
Ch1_
Example 5
This example illustrates a system that has no solution. Let us try to solve the system
Solution
The system has no solution.

Ch1_
Ch1_
Homogeneous System of linear Equations
Definition
A system of linear equations is said to be homogeneous if all the constant terms are zeros.

Ch1_
Ch1_
Homogeneous System of linear Equations
Note. Non trivial solution

Ch1_
Ch1_
Homework
Exercise will be given by the teachers of the practical classes.

Ch1_
1.3 Gaussian Elimination
Definition
A matrix is in echelon form if
Any rows consisting entirely of zeros are grouped at the bottom of the matrix.
The first nonzero element of each row is 1. This element is called a leading 1.
The leading 1 of each row after the first is positioned to the right of the leading 1 of the previous row.
(This implies that all the elements below a leading 1 are zero.)

Ch1_
Example 6
Solving the following system of linear equations using the method of Gaussian elimination.
Solution
We have arrived at the echelon form.

Ch1_
The corresponding system of equation is

Ch1_
Example 7
Solving the following system of linear equations using the method of Gaussian elimination, performing back substitution using matrices.
Solution
This marks the end of the forward elimination of variables from equations. We now commence the back substitution using matrices.