Слайд 2Angular momentum. Moment of inertia and more properties of angular motion.

Слайд 3Moment of inertia, I
For linear momentum, p = mv
Similarly, for angular momentum,

L = “something”x ω
That is, we seek a property of the body that measures ‘angular inertia’. This is defined as the moment of inertia, I.
Thus: L = I ω
Слайд 4One way to get a formula for I
Consider a body rotating with
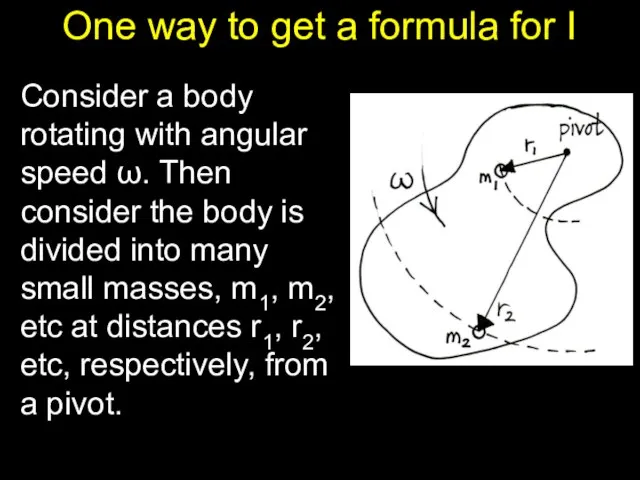
angular speed ω. Then consider the body is divided into many small masses, m1, m2, etc at distances r1, r2, etc, respectively, from a pivot.
Слайд 5Moment of inertia
is the angular speed

Слайд 7More on I
Note: we know that 1) if no external forces act

on the system, linear momentum is conserved.
We now know that 2) if no external torques act on the system, angular momentum is conserved. This explains why, e.g., an ice skater rotates faster when she pulls in her arms.
Слайд 8Conservation of angular momentum
Since L = I ω, if no external torques

act, L is constant.
So, when the skater moves her arms in, closer to her body,
I decreases and therefore ω increases.
Слайд 9Conservation of angular momentum
In (1) I = m1a2 +m2a2
In (2) I =
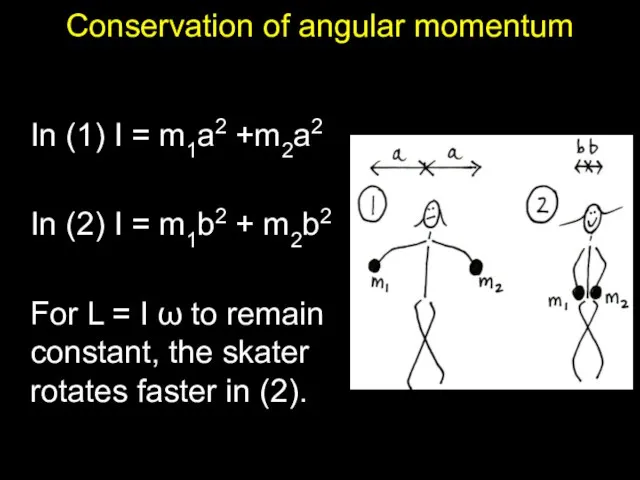
m1b2 + m2b2
For L = I ω to remain constant, the skater rotates faster in (2).
Слайд 10Please don’t try this!
A crazy physics professor stands on a swivel chair

with weights in his outstretched arms. A student causes him to rotate.
The professor brings in his arms and…
Слайд 11Comparison of equations for linear and angular motion

Слайд 12Example 1. Conservation of angular momentum
A horizontal disc rotates around a vertical

axis at 90 rev/min. A small piece of chewing gum of 20 g falls vertically onto the disc and sticks to it at a distance of 5.0 cm from the axis. If the number of revs/min is reduced to 80, find the moment of inertia, I, of the disc.
Слайд 13Work done by torque
Note: We can also define work done by a

constant torque in moving through an angle θ as: W = τθ
The power
Слайд 14Example 2
An electric motor supplies a power of 500 W to drive

a flywheel of I = 2.0 kgm2 at a speed of 600 rev/min. How long will it take the flywheel to come to rest after the power is switched off, assuming the retarding torque, due to friction, is constant?














 Основные права военнослужащих
Основные права военнослужащих Королевская семья Великобритании
Королевская семья Великобритании Составь пословицу. Как ты понимаешь эту пословицу? МОЙ ДОММОЯ КРЕПОСТЬ.
Составь пословицу. Как ты понимаешь эту пословицу? МОЙ ДОММОЯ КРЕПОСТЬ. Понятие права. Функции права
Понятие права. Функции права Общественное участие в бюджетном процессе и городских целевых программах
Общественное участие в бюджетном процессе и городских целевых программах Анализ методической работы за 2019-2020 учебный год по учебному предмету Трудовое обучение
Анализ методической работы за 2019-2020 учебный год по учебному предмету Трудовое обучение Поезд Здоровья. Жемчужина России
Поезд Здоровья. Жемчужина России Мутагены
Мутагены «ЦЕНТР ЮНОШЕСКОГОНАУЧНО-ТЕХНИЧЕСКОГО ТВОРЧЕСТВА»
«ЦЕНТР ЮНОШЕСКОГОНАУЧНО-ТЕХНИЧЕСКОГО ТВОРЧЕСТВА» Презентация на тему Межличностные отношения
Презентация на тему Межличностные отношения Beden Aluminium
Beden Aluminium Человек как предмет комплексного, целостного философско-научного исследования
Человек как предмет комплексного, целостного философско-научного исследования История и символы Олимпийских игр
История и символы Олимпийских игр Решение расчётных задач по химии
Решение расчётных задач по химии Программы развития классного коллектива 3 «В» класса МОУ «ВСОШ№2»
Программы развития классного коллектива 3 «В» класса МОУ «ВСОШ№2» Влияние стресса на здоровье студентов
Влияние стресса на здоровье студентов Космическое путешествие на планету лингвистика
Космическое путешествие на планету лингвистика Как сделать хорошую презентацию
Как сделать хорошую презентацию  Изучение объектов природы в процессе взаимоотношений с окружающим
Изучение объектов природы в процессе взаимоотношений с окружающим Урок математики
Урок математики Туган нигез төшенчәсен ничек аңлыйсыз
Туган нигез төшенчәсен ничек аңлыйсыз Франция. Долгий путь к единству
Франция. Долгий путь к единству Презентация на тему Опасные природные явления
Презентация на тему Опасные природные явления 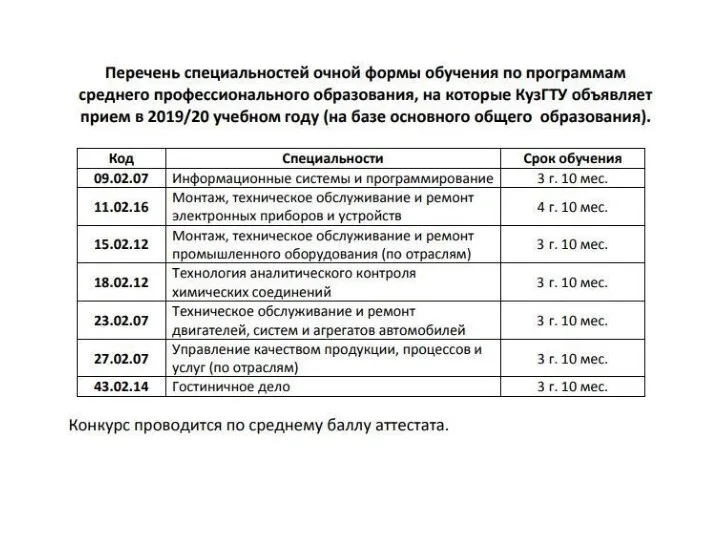 КузГТУ. Прием в 2019-2020 учебном году. Перечень специальностей
КузГТУ. Прием в 2019-2020 учебном году. Перечень специальностей Бабочки-Монархи
Бабочки-Монархи Заливочные полимерные материалы
Заливочные полимерные материалы Экология и фитодизайн школьного кабинета биологии
Экология и фитодизайн школьного кабинета биологии Теоретико-методологічні основи розвитку асортименту послуг бібліотек
Теоретико-методологічні основи розвитку асортименту послуг бібліотек